Control 3 Mate III 2009 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa de Enseñanza Media > Escuela de Verano > Escuela de Verano > Matemática > Matemáticas III

Reply to this topic

Start new topic

Control 3 Mate III 2009

rock&mati rock&mati Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 23 2009, 08:40 PM Publicado: #1
Dios Matemático Grupo: Usuario FMAT Mensajes: 316 Registrado: 2-May 08 Desde: a la &$€¬~#@ del mundo Miembro Nº: 21.900 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaqjEa<br />% qaaiaabcfacaqGXaGaaeOlaiaab2caaaaabaGaaeikaiaabggacaqG<br />% PaGaaeiiaiaabccacaqGdbGaae4Baiaab6gacaqGZbGaaeyAaiaabs<br />% gacaqGLbGaaeOCaiaabwgacaqGGaGaaeiBaiaabggacaqGGaGaaeOz<br />% aiaabwhacaqGUbGaae4yaiaabMgacaqGVbGaaeOBaiaabccacaWGNb<br />% GaaiikaiaadIhacaGGPaGaeyypa0ZaaSaaaeaacaWG4bGaey4kaSIa<br />% aGymaaqaaiaadIhacqGHsislcaaIXaaaaiaab6cacaqGGaGaaeyrai<br />% aab6gacaqGJbGaaeyDaiaabwgacaqGUbGaaeiDaiaabkhacaqGLbGa<br />% aeiiaiaabohacaqG1bGaaeiiaiaabsgacaqGVbGaaeyBaiaabMgaca<br />% qGUbGaaeyAaiaab+gacaqGSaGaaeiiaiaabogacaqGLbGaaeOCaiaa<br />% b+gacaqGZbGaaeiiaiaabMhacaqGGaGaaeyyaiaabohacaqGPbGaae<br />% OBaiaabshacaqGVbGaaeiDaiaabggacaqGZbGaaeiiaiaabsgacaqG<br />% LbGaaeiiaiaabshacaqGVbGaaeizaiaab+gacaqGGaGaaeiDaiaabM<br />% gacaqGWbGaae4Baiaab6caaeaacaqGOaGaaeOyaiaabMcacaqGGaGa<br />% aeiiaiaabofacaqGLbGaaeyyaiaabccacqaHXoqycaGGSaGaeqOSdi<br />% MaeyicI4SaeSyhHeQaaeOlaiaabccacaqGfbGaaeOBaiaabogacaqG<br />% 1bGaaeyzaiaab6gacaqG0bGaaeOCaiaabwgacaqGGaGaaeyDaiaab6<br />% gacaqGHbGaaeiiaiaabkhacaqGLbGaaeiBaiaabggacaqGJbGaaeyA<br />% aiaab+gacaqGUbGaaeiiaiaabwgacaqGUbGaaeiDaiaabkhacaqGLb<br />% GaaeiiaiaabwgacaqGSbGaaeiBaiaab+gacaqGZbGaaeiiaiaabsga<br />% caqGLbGaaeiiaiaab2gacaqGVbGaaeizaiaab+gacaqGGaGaaeyCai<br />% aabwhacaqGLbGaaeiiaiaabYgacaqGHbGaaeiiaiaabAgacaqG1bGa<br />% aeOBaiaabogacaqGPbGaae4Baiaab6gacaqG6aaabaGaaeiiaiaabc<br />% cacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeii<br />% aiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGa<br />% GaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabcca<br />% caqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiai<br />% aabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGa<br />% aeiiaiaabccacaWGMbGaaiikaiaadIhacaGGPaGaeyypa0Zaaiqaaq<br />% aabeqaamaalaaabaGaci4CaiaacMgacaGGUbGaaiikaiabeg7aHjaa<br />% dIhadaahaaWcbeqaaiaaikdaaaGccaGGPaaabaGaciiDaiaacggaca<br />% GGUbGaaiikaiaadIhadaahaaWcbeqaaiaaikdaaaGccaGGPaaaaiaa<br />% bccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaae<br />% iiaiaabccacaqGZbGaaeyAaiaabccacaWG4bGaeyipaWJaaGimaaqa<br />% aiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcqaHYoGycaWG4b<br />% Gaey4kaSIaeqOSdiMaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqG<br />% GaGaaeiiaiaabccacaqGZbGaaeyAaiaabccacaWG4bGaeyyzImRaaG<br />% imaaaacaGL7baacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabcca<br />% caqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiai<br />% aabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGa<br />% aeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccaca<br />% qGGaGaaeiiaiaabccacaqGGaGaaeiiaaqaaiaabccacaqGGaGaaeii<br />% aiaabccacaqGGaGaaeiiaiaabohacaqGLbGaaeyyaiaabccacaqGJb<br />% Gaae4Baiaab6gacaqG0bGaaeyAaiaab6gacaqG1bGaaeyyaiaabcca<br />% caqGLbGaaeOBaiaabccacaqG0bGaae4BaiaabsgacaqGVbGaaeiiai<br />% aabohacaqG1bGaaeiiaiaabsgacaqGVbGaaeyBaiaabMgacaqGUbGa<br />% aeyAaiaab+gacaqGUaaaaaa!4EEF!<br />\[<br />\begin{gathered}<br /> \boxed{{\text{P1}}{\text{. - }}} \hfill \\<br /> {\text{(a) Considere la funcion }}g(x) = \frac{{x + 1}}<br />{{x - 1}}{\text{. Encuentre su dominio}}{\text{, ceros y asintotas de todo tipo}}{\text{.}} \hfill \\<br /> {\text{(b) Sea }}\alpha ,\beta \in \mathbb{R}{\text{. Encuentre una relacion entre ellos de modo que la funcion:}} \hfill \\<br /> {\text{ }}f(x) = \left\{ \begin{gathered}<br /> \frac{{\sin (\alpha x^2 )}}<br />{{\tan (x^2 )}}{\text{ si }}x < 0 \hfill \\<br /> x^2 + \beta x + \beta {\text{ si }}x \geqslant 0 \hfill \\ <br />\end{gathered} \right.{\text{ }} \hfill \\<br /> {\text{ sea continua en todo su dominio}}{\text{.}} \hfill \\ <br />\end{gathered} <br />\]$ $TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaqjEa<br />% qaaiaabcfacaqGYaGaaeOlaiaab2caaaaabaaabaGaaeikaiaabgga<br />% caqGPaGaaeiiaiaabccacaqGdbGaaeyyaiaabYgacaqGJbGaaeyDai<br />% aabYgacaqGLbGaaeiiaiaabYgacaqGVbGaae4CaiaabccacaqGZbGa<br />% aeyAaiaabEgacaqG1bGaaeyAaiaabwgacaqGUbGaaeiDaiaabwgaca<br />% qGZbGaaeiiaiaabYgacaqGPbGaaeyBaiaabMgacaqG0bGaaeyzaiaa<br />% bohacaqG6aaabaGaaeikaiaabMgacaqGPaWaaCbeaeaaciGGSbGaai<br />% yAaiaac2gaaSqaaiaad6gacqGHsgIRcqGHEisPaeqaaOWaaOaaaeaa<br />% daWcaaqaaiaadwgadaahaaWcbeqaamaabmaabaWaaSqaaWqaaiaaig<br />% daaeaacaWGUbaaaaWccaGLOaGaayzkaaWaaWbaaWqabeaacaaIYaaa<br />% aaaakiabgkHiTiaaigdaaeaadaqadaqaamaaleaaleaacaaIXaaaba<br />% GaamOBaaaaaOGaayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaaaaaa<br />% beaaaOqaaiaabIcacaqGPbGaaeyAaiaabMcadaWfqaqaaiGacYgaca<br />% GGPbGaaiyBaaWcbaGaamiEaiabgkziUkabgUcaRiabg6HiLcqabaGc<br />% daWcaaqaamaabmaabaGaamiEaiabgkHiTiaaigdaaiaawIcacaGLPa<br />% aadaahaaWcbeqaaiaaiodaaaGccqGHsislcaWG4bWaaWbaaSqabeaa<br />% caaIZaaaaaGcbaWaaOaaaeaadaGcaaqaaiaaiwdaaSqabaGccaWG4b<br />% Gaey4kaSIaaG4maiaadIhadaahaaWcbeqaaiaaisdaaaaabeaaaaaa<br />% keaaaeaacaqGOaGaaeOyaiaabMcacaqGGaGaaeiiaiaabofacaqGLb<br />% Gaaeyyaiaab6gacaqGGaGaamyyamaaBaaaleaacaaIWaaabeaakiaa<br />% bYcacaWGHbWaaSbaaSqaaiaaigdaaeqaaOGaaeilaiaadggadaWgaa<br />% WcbaGaaGOmaaqabaGccqGHiiIZcqWIDesOcaqGUaGaaeiiaiaabofa<br />% caqGLbGaaeiiaiaabsgacaqGLbGaaeOzaiaabMgacaqGUbGaaeyzai<br />% aabccacaqGSbGaaeyyaiaabccacaqGMbGaaeyDaiaab6gacaqGJbGa<br />% aeyAaiaab+gacaqGUbGaaeiiaiaab2gacaqGLbGaaeizaiaabMgaca<br />% qGHbGaaeOBaiaabshacaqGLbGaaeiiaiaadAgacaGGOaGaamiEaiaa<br />% cMcacqGH9aqpcaWGHbWaaSbaaSqaaiaaicdaaeqaaOGaey4kaSIaam<br />% yyamaaBaaaleaacaaIXaaabeaakiaadIhacqGHRaWkcaWGHbWaaSba<br />% aSqaaiaaikdaaeqaaOGaamiEamaaCaaaleqabaGaaGOmaaaakiabgk<br />% HiTiaaiwdacaWG4bWaaWbaaSqabeaacaaIZaaaaaGcbaGaaeikaiaa<br />% bMgacaqGPaGaaeiiaiaab2eacaqG1bGaaeyzaiaabohacaqG0bGaae<br />% OCaiaabwgacaqGGaGaaeyCaiaabwhacaqGLbGaaeiiamaaxababaGa<br />% ciiBaiaacMgacaGGTbaaleaacaWG4bGaeyOKH4Qaey4kaSIaeyOhIu<br />% kabeaakiaadAgacaGGOaGaamiEaiaacMcacqGH9aqpcqGHsislcqGH<br />% EisPcqGHNis2daWfqaqaaiGacYgacaGGPbGaaiyBaaWcbaGaamiEai<br />% abgkziUkabgkHiTiabg6HiLcqabaGccaWGMbGaaiikaiaadIhacaGG<br />% PaGaeyypa0JaeyOhIukabaGaaeikaiaabMgacaqGPbGaaeykaiaabc<br />% cacaqGGaGaae4qaiaab+gacaqGUbGaae4yaiaabYgacaqG1bGaaeyE<br />% aiaabggacaqGGaGaaeyCaiaabwhacaqGLbGaaeiiaiabgoGiKiaadg<br />% gacaGGSaGaamOyaiabgIGiolabl2riHkaabccacaqG0bGaaeyyaiaa<br />% bYgacaqGLbGaae4CaiaabccacaqGXbGaaeyDaiaabwgacaqGGaGaam<br />% yyaiabgYda8iaadkgacaGGSaGaamOzaiaacIcacaWGHbGaaiykaiab<br />% g6da+iaaicdacaqGGaGaaeyEaiaabccacaWGMbGaaiikaiaadkgaca<br />% GGPaGaeyipaWJaaGimaiaab6caaeaacaqGOaGaaeyAaiaabMgacaqG<br />% PbGaaeykaiaabccacaqGGaGaaeiraiaabwgacaqGTbGaaeyDaiaabw<br />% gacaqGZbGaaeiDaiaabkhacaqGLbGaaeiiaiaabghacaqG1bGaaeyz<br />% aiaabccacaGGOaGaey4aIqYaa0aaaeaacaWG4baaaiabgIGiolabl2<br />% riHkaacMcacaWGMbGaaiikamaanaaabaGaamiEaaaacaGGPaGaeyyp<br />% a0JaaGimaiaac6caaaaa!3F7D!<br />\[<br />\begin{gathered}<br /> \boxed{{\text{P2}}{\text{. - }}} \hfill \\<br /> \hfill \\<br /> {\text{(a) Calcule los siguientes limites:}} \hfill \\<br /> {\text{(i)}}\mathop {\lim }\limits_{n \to \infty } \sqrt {\frac{{e^{\left( {\tfrac{1}<br />{n}} \right)^2 } - 1}}<br />{{\left( {\tfrac{1}<br />{n}} \right)^2 }}} \hfill \\<br /> {\text{(ii)}}\mathop {\lim }\limits_{x \to + \infty } \frac{{\left( {x - 1} \right)^3 - x^3 }}<br />{{\sqrt {\sqrt 5 x + 3x^4 } }} \hfill \\<br /> \hfill \\<br /> {\text{(b) Sean }}a_0 {\text{,}}a_1 {\text{,}}a_2 \in \mathbb{R}{\text{. Se define la funcion mediante }}f(x) = a_0 + a_1 x + a_2 x^2 - 5x^3 \hfill \\<br /> {\text{(i) Muestre que }}\mathop {\lim }\limits_{x \to + \infty } f(x) = - \infty \wedge \mathop {\lim }\limits_{x \to - \infty } f(x) = \infty \hfill \\<br /> {\text{(ii) Concluya que }}\exists a,b \in \mathbb{R}{\text{ tales que }}a < b,f(a) > 0{\text{ y }}f(b) < 0. \hfill \\<br /> {\text{(iii) Demuestre que }}(\exists \overline x \in \mathbb{R})f(\overline x ) = 0. \hfill \\ <br />\end{gathered} <br />\]$ $TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaqjEa<br />% qaaiaabcfacaqGZaGaaeOlaiaab2caaaaabaGaae4uaiaabwgacaqG<br />% HbGaaeOBaiaabccadaqadaqaaiaadggadaWgaaWcbaGaamOBaaqaba<br />% aakiaawIcacaGLPaaadaWgaaWcbaGaamOBaiabgIGiolablwriLcqa<br />% baGccaqGSaWaaeWaaeaacaWGIbWaaSbaaSqaaiaad6gaaeqaaaGcca<br />% GLOaGaayzkaaWaaSbaaSqaaiaad6gacqGHiiIZcqWIvesPaeqaaOGa<br />% aeiiaiaabohacaqG1bGaae4yaiaabwgacaqGZbGaaeyAaiaab+gaca<br />% qGUbGaaeyzaiaabohacaqGGaGaaeOCaiaabwgacaqGHbGaaeiBaiaa<br />% bwgacaqGZbGaaeiiaiaabshacaqGHbGaaeiBaiaabwgacaqGZbGaae<br />% iiaiaabghacaqG1bGaaeyzaiaabccacaWGHbWaaSbaaSqaaiaad6ga<br />% aeqaaOGaaeiiaiaabwgacaqGZbGaaeiiaiaabogacaqGYbGaaeyzai<br />% aabogacaqGPbGaaeyzaiaab6gacaqG0bGaaeyzaiaabYcacaqGGaGa<br />% amOyamaaBaaaleaacaWGUbaabeaakiaabccacaqGLbGaae4Caiaabc<br />% cacaqGKbGaaeyzaiaabogacaqGYbGaaeyzaiaabogacaqGPbGaaeyz<br />% aiaab6gacaqG0bGaaeyzaiaabccacaqG5baabaGaamyyamaaBaaale<br />% aacaWGUbaabeaakiabgsMiJkaadkgadaWgaaWcbaGaamOBaaqabaGc<br />% caqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiai<br />% aabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGa<br />% aeiiaiaabccacqGHaiIicaWGUbGaeyicI4SaeSyfHukabaGaaeikai<br />% aabggacaqGPaGaaeiiaiaabccacaqGtbGaaeyAaiaabccacaWGbbGa<br />% eyypa0ZaaiWaaeaadaabcaqaaiaadggadaWgaaWcbaGaamOBaaqaba<br />% aakiaawIa7aiaad6gacqGHiiIZcqWIvesPaiaawUhacaGL9baacaqG<br />% GaGaaeyEaiaabccacaWGcbGaeyypa0ZaaiWaaeaadaabcaqaaiaadk<br />% gadaWgaaWcbaGaamOBaaqabaaakiaawIa7aiaad6gacqGHiiIZcqWI<br />% vesPaiaawUhacaGL9baacaqGGaGaaeilaiaabsgacaqGLbGaaeyBai<br />% aabwhacaqGLbGaae4CaiaabshacaqGYbGaaeyzaiaabccacaqGXbGa<br />% aeyDaiaabwgacaqGGaGaae4CaiaabwhacaqGWbGaaiikaiaadgeaca<br />% GGPaGaeyizImQaaeyAaiaab6gacaqGMbGaaiikaiaadkeacaGGPaaa<br />% baGaaeikaiaabkgacaqGPaGaaeiiaiaabccacaqGdbGaae4Baiaab6<br />% gacaqGJbGaaeiBaiaabwhacaqG5bGaaeyyaiaabccacaqGXbGaaeyD<br />% aiaabwgacaqGGaGaey4aIqIaam4yaiabgIGiolabl2riHkaabccaca<br />% qG0bGaaeyyaiaabYgacaqGGaGaaeyCaiaabwhacaqGLbGaaeiiaiaa<br />% dogacaqGGaGaaeyzaiaabohacaqGGaGaaeyDaiaab6gacaqGHbGaae<br />% iiaiaabogacaqGVbGaaeiDaiaabggacaqGGaGaae4CaiaabwhacaqG<br />% WbGaaeyzaiaabkhacaqGPbGaae4BaiaabkhacaqGGaGaaeizaiaabw<br />% gacaqGGaGaamyqaiaabccacaqG5bGaaeiiaiaabggacaqGGaGaaeiB<br />% aiaabggacaqGGaGaaeODaiaabwgacaqG6bGaaeilaiaabccacaqGJb<br />% Gaae4BaiaabshacaqGHbGaaeiiaiaabMgacaqGUbGaaeOzaiaabwga<br />% caqGYbGaaeyAaiaab+gacaqGYbGaaeiiaiaabsgacaqGLbGaaeiiai<br />% aadkeaaeaacaqGOaGaae4yaiaabMcacaqGGaGaaeiiaiaabofacaqG<br />% 1bGaaeiCaiaab+gacaqGUbGaae4zaiaabggacaqGGaGaaeyyaiaabI<br />% gacaqGVbGaaeOCaiaabggacaqGGaGaaeyCaiaabwhacaqGLbGaaeii<br />% amaaxababaGaciiBaiaacMgacaGGTbaaleaacaWGUbGaeyOKH4Qaey<br />% OhIukabeaakmaabmaabaGaamyyamaaBaaaleaacaWGUbaabeaakiab<br />% gkHiTiaadkgadaWgaaWcbaGaamOBaaqabaaakiaawIcacaGLPaaacq<br />% GH9aqpcaaIWaGaaeOlaiaabccacaqGGaGaaeiraiaabwgacaqGTbGa<br />% aeyDaiaabwgacaqGZbGaaeiDaiaabkhacaqGLbGaaeiiaiaabghaca<br />% qG1bGaaeyzaiaabccacaqGLbGaaeiBaiaabccacaWGJbGaaeiiaiaa<br />% bsgacaqGLbGaaeiiaiaabYgacaqGHbGaaeiiaiaabchacaqGHbGaae<br />% OCaiaabshacaqGLbGaaeiiaiaabggacaqGUbGaaeiDaiaabwgacaqG<br />% YbGaaeyAaiaab+gacaqGYbGaaeiiaiaabwgacaqGZbGaaeiiaiaabw<br />% hacaqGUbGaaeyAaiaabogacaqGVbaaaaa!70D1!<br />\[<br />\begin{gathered}<br /> \boxed{{\text{P3}}{\text{. - }}} \hfill \\<br /> {\text{Sean }}\left( {a_n } \right)_{n \in \mathbb{N}} {\text{,}}\left( {b_n } \right)_{n \in \mathbb{N}} {\text{ sucesiones reales tales que }}a_n {\text{ es creciente}}{\text{, }}b_n {\text{ es decreciente y}} \hfill \\<br /> a_n \leqslant b_n {\text{ }}\forall n \in \mathbb{N} \hfill \\<br /> {\text{(a) Si }}A = \left\{ {\left. {a_n } \right\|n \in \mathbb{N}} \right\}{\text{ y }}B = \left\{ {\left. {b_n } \right\|n \in \mathbb{N}} \right\}{\text{ }}{\text{,demuestre que sup}}(A) \leqslant {\text{inf}}(B) \hfill \\<br /> {\text{(b) Concluya que }}\exists c \in \mathbb{R}{\text{ tal que }}c{\text{ es una cota superior de }}A{\text{ y a la vez}}{\text{, cota inferior de }}B \hfill \\<br /> {\text{© Suponga ahora que }}\mathop {\lim }\limits_{n \to \infty } \left( {a_n - b_n } \right) = 0.{\text{ Demuestre que el }}c{\text{ de la parte anterior es unico}} \hfill \\ <br />\end{gathered} <br />\]$ Mensaje modificado por rock&mati el Jan 23 2009, 08:43 PM

rock&mati rock&mati Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 23 2009, 08:40 PM Publicado: #2
Dios Matemático Grupo: Usuario FMAT Mensajes: 316 Registrado: 2-May 08 Desde: a la &$€¬~#@ del mundo Miembro Nº: 21.900 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaqjEa<br />% qaaiaabcfacaqGYaGaaeOlaiaab2cacaqGcbaaaaqaaiaabIeacaqG<br />% HbGaaeyEaiaabccacaqGXbGaaeyDaiaabwgacaqGGaGaaeOBaiaab+<br />% gacaqG0bGaaeyyaiaabkhacaqGGaGaaeyCaiaabwhacaqGLbGaaeii<br />% aiaabchacaqGHbGaaeOCaiaabggacaqGGaGaaeyCaiaabwhacaqGLb<br />% GaaeiiaiaabAgacaqG1bGaaeOBaiaabogacaqGPbGaae4Baiaab6ga<br />% caqGGaGaae4CaiaabwgacaqGHbGaaeiiaiaabogacaqGVbGaaeOBai<br />% aabshacaqGPbGaaeOBaiaabwhacaqGHbGaaeilaiaabccacaqGZbGa<br />% aeyDaiaabohacaqGGaGaaeiBaiaabMgacaqGTbGaaeyAaiaabshaca<br />% qGLbGaae4CaiaabccacaqGSbGaaeyyaiaabshacaqGLbGaaeOCaiaa<br />% bggacaqGSbGaaeyzaiaabohacaqGGaGaaeizaiaabwgacaqGIbGaae<br />% yzaiaab6gacaqGGaGaae4CaiaabwgacaqGYbGaaeiiaiaabMgacaqG<br />% NbGaaeyDaiaabggacaqGSbGaaeyzaiaabohaaeaacaqGJbGaaeyDai<br />% aabggacaqGUbGaaeizaiaab+gacaqGGaGaamiEaiabgkziUkaaicda<br />% caGGUaaabaWaaCbeaeaaciGGSbGaaiyAaiaac2gaaSqaaiaadIhacq<br />% GHsgIRcaaIWaWaaWbaaWqabeaacqGHsislaaaaleqaaOWaaeWaaeaa<br />% daWcaaqaaiGacohacaGGPbGaaiOBaiaacIcacqaHXoqycaWG4bWaaW<br />% baaSqabeaacaaIYaaaaOGaaiykaaqaaiGacshacaGGHbGaaiOBaiaa<br />% cIcacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaaiykaaaaaiaawIcaca<br />% GLPaaacaqGGaGaeyypa0ZaaCbeaeaaciGGSbGaaiyAaiaac2gaaSqa<br />% aiaadIhacqGHsgIRcaaIWaWaaWbaaWqabeaacqGHRaWkaaaaleqaaO<br />% WaaeWaaeaacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaeqOS<br />% diMaamiEaiabgUcaRiabek7aIbGaayjkaiaawMcaaaqaaaqaaiaabA<br />% facaqGLbGaaeyyaiaab2gacaqGVbGaae4CaiaabccacaqGWbGaaeOC<br />% aiaabMgacaqGTbGaaeyzaiaabkhacaqGVbGaaeiiaiaabwgacaqGSb<br />% GaaeiiaiaabYgacaqGPbGaaeyBaiaabMgacaqG0bGaaeyzaiaabcca<br />% caqGWbGaae4BaiaabkhacaqGGaGaaeiBaiaabggacaqGGaGaaeyAai<br />% aabQhacaqGXbGaaeyDaiaabMgacaqGLbGaaeOCaiaabsgacaqGHbGa<br />% aeOoaaqaamaaxababaGaciiBaiaacMgacaGGTbaaleaacaWG4bGaey<br />% OKH4QaaGimamaaCaaameqabaGaeyOeI0caaaWcbeaakmaabmaabaWa<br />% aSaaaeaaciGGZbGaaiyAaiaac6gacaGGOaGaeqySdeMaamiEamaaCa<br />% aaleqabaGaaGOmaaaakiaacMcaaeaaciGG0bGaaiyyaiaac6gacaGG<br />% OaGaamiEamaaCaaaleqabaGaaGOmaaaakiaacMcaaaaacaGLOaGaay<br />% zkaaGaeyypa0ZaaCbeaeaaciGGSbGaaiyAaiaac2gaaSqaaiaadIha<br />% cqGHsgIRcaaIWaWaaWbaaWqabeaacqGHsislaaaaleqaaOWaaeWaae<br />% aadaWcaaqaaiGacohacaGGPbGaaiOBaiaacIcacqaHXoqycaWG4bWa<br />% aWbaaSqabeaacaaIYaaaaOGaaiykaiabgwSixlGacogacaGGVbGaai<br />% 4CaiaacIcacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaaiykaaqaaiGa<br />% cohacaGGPbGaaiOBaiaacIcacaWG4bWaaWbaaSqabeaacaaIYaaaaO<br />% GaaiykaaaaaiaawIcacaGLPaaacqGH9aqpdaWfqaqaaiGacYgacaGG<br />% PbGaaiyBaaWcbaGaamiEaiabgkziUkaaicdadaahaaadbeqaaiabgk<br />% HiTaaaaSqabaGcdaqadaqaamaalaaabaGaci4CaiaacMgacaGGUbGa<br />% aiikaiabeg7aHjaadIhadaahaaWcbeqaaiaaikdaaaGccaGGPaGaey<br />% yXICTaci4yaiaac+gacaGGZbGaaiikaiaadIhadaahaaWcbeqaaiaa<br />% ikdaaaGccaGGPaaabaGaci4CaiaacMgacaGGUbGaaiikaiaadIhada<br />% ahaaWcbeqaaiaaikdaaaGccaGGPaaaaiabgwSixpaalaaabaWaaSqa<br />% aSqaaiaaigdaaeaacaWG4bWaaWbaaWqabeaacaaIYaaaaaaaaOqaam<br />% aaleaaleaacaaIXaaabaGaamiEamaaCaaameqabaGaaGOmaaaaaaaa<br />% aaGccaGLOaGaayzkaaaabaGaeyi1HS9aaCbeaeaaciGGSbGaaiyAai<br />% aac2gaaSqaaiaadIhacqGHsgIRcaaIWaWaaWbaaWqabeaacqGHsisl<br />% aaaaleqaaOWaaeWaaeaadaWcaaqaamaalaaabaGaci4CaiaacMgaca<br />% GGUbGaaiikaiabeg7aHjaadIhadaahaaWcbeqaaiaaikdaaaGccaGG<br />% PaGaeyyXICTaci4yaiaac+gacaGGZbGaaiikaiaadIhadaahaaWcbe<br />% qaaiaaikdaaaGccaGGPaaabaGaamiEamaaCaaaleqabaGaaGOmaaaa<br />% aaGccqGHflY1daWcaaqaaiabeg7aHbqaaiabeg7aHbaaaeaadaWcaa<br />% qaaiGacohacaGGPbGaaiOBaiaacIcacaWG4bWaaWbaaSqabeaacaaI<br />% YaaaaOGaaiykaaqaaiaadIhadaahaaWcbeqaaiaaikdaaaaaaaaaaO<br />% GaayjkaiaawMcaaiabg2da9maaxababaGaciiBaiaacMgacaGGTbaa<br />% leaacaWG4bGaeyOKH4QaaGimamaaCaaameqabaGaeyOeI0caaaWcbe<br />% aakmaabmaabaWaaSaaaeaadaagbaqaamaalaaabaGaeqySdeMaci4C<br />% aiaacMgacaGGUbGaaiikaiabeg7aHjaadIhadaahaaWcbeqaaiaaik<br />% daaaGccaGGPaaabaGaeqySdeMaamiEamaaCaaaleqabaGaaGOmaaaa<br />% aaaabaGaeyOKH4QaeqySdegakiaawEJ-aiabgwSixpaayeaabaGaci<br />% 4yaiaac+gacaGGZbGaaiikaiaadIhadaahaaWcbeqaaiaaikdaaaGc<br />% caGGPaaaleaacqGHsgIRcaaIXaaakiaawEJ-aaqaamaayaaabaWaaS<br />% aaaeaaciGGZbGaaiyAaiaac6gacaGGOaGaamiEamaaCaaaleqabaGa<br />% aGOmaaaakiaacMcaaeaacaWG4bWaaWbaaSqabeaacaaIYaaaaaaaae<br />% aacqGHsgIRcaaIXaaakiaawIJ-aaaaaiaawIcacaGLPaaacqGH9aqp<br />% cqaHXoqyaeaacaqGwbGaaeyzaiaabggacaqGTbGaae4Baiaabohaca<br />% qGGaGaaeyyaiaabIgacaqGVbGaaeOCaiaabggacaqGGaGaaeyzaiaa<br />% bYgacaqGGaGaaeiBaiaabMgacaqGTbGaaeyAaiaabshacaqGLbGaae<br />% iiaiaabchacaqGVbGaaeOCaiaabccacaqGSbGaaeyyaiaabccacaqG<br />% KbGaaeyzaiaabkhacaqGLbGaae4yaiaabIgacaqGHbGaaeOoaaqaam<br />% aaxababaGaciiBaiaacMgacaGGTbaaleaacaWG4bGaeyOKH4QaaGim<br />% amaaCaaameqabaGaey4kaScaaaWcbeaakmaabmaabaWaaGbaaeaaca<br />% WG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaeqOSdiMaamiEaaWc<br />% baGaeyOKH4QaaGimaaGccaGL44pacqGHRaWkcqaHYoGyaiaawIcaca<br />% GLPaaacqGH9aqpcqaHYoGyaeaaaeaacaqGdbGaae4Baiaab2gacaqG<br />% VbGaaeiiaiaabYgacaqGVbGaae4CaiaabccacaqGSbGaaeyAaiaab2<br />% gacaqGPbGaaeiDaiaabwgacaqGZbGaaeiiaiaabYgacaqGHbGaaeiD<br />% aiaabwgacaqGYbGaaeyyaiaabYgacaqGLbGaae4CaiaabccacaqGKb<br />% GaaeyzaiaabkgacaqGLbGaaeOBaiaabccacaqGZbGaaeyzaiaabkha<br />% caqGGaGaaeyAaiaabEgacaqG1bGaaeyyaiaabYgacaqGLbGaae4Cai<br />% aabccacaqGWbGaaeyyaiaabkhacaqGHbGaaeiiaiaabghacaqG1bGa<br />% aeyzaiaabccacaqGSbGaaeyyaiaabccacaqGMbGaaeyDaiaab6gaca<br />% qGJbGaaeyAaiaab+gacaqGUbGaaeiiaiaabohacaqGLbGaaeyyaiaa<br />% bccacaqGJbGaae4Baiaab6gacaqG0bGaaeyAaiaab6gacaqG1bGaae<br />% yyaiaabYcacaqGGaGaae4yaiaab+gacaqGUbGaae4yaiaabYgacaqG<br />% 1bGaaeyAaiaab2gacaqGVbGaae4CaaqaaiaabghacaqG1bGaaeyzai<br />% aabccacqaHXoqycqGH9aqpcqaHYoGycaGGUaaaaaa!3800!<br />\[<br />\begin{gathered}<br /> \boxed{{\text{P1}}{\text{. - B}}} \hfill \\<br /> {\text{Hay que notar que para que funcion sea continua}}{\text{, sus limites laterales deben ser iguales}} \hfill \\<br /> {\text{cuando }}x \to 0. \hfill \\<br /> \mathop {\lim }\limits_{x \to 0^ - } \left( {\frac{{\sin (\alpha x^2 )}}<br />{{\tan (x^2 )}}} \right){\text{ }} = \mathop {\lim }\limits_{x \to 0^ + } \left( {x^2 + \beta x + \beta } \right) \hfill \\<br /> \hfill \\<br /> {\text{Veamos primero el limite por la izquierda:}} \hfill \\<br /> \mathop {\lim }\limits_{x \to 0^ - } \left( {\frac{{\sin (\alpha x^2 )}}<br />{{\tan (x^2 )}}} \right) = \mathop {\lim }\limits_{x \to 0^ - } \left( {\frac{{\sin (\alpha x^2 ) \cdot \cos (x^2 )}}<br />{{\sin (x^2 )}}} \right) = \mathop {\lim }\limits_{x \to 0^ - } \left( {\frac{{\sin (\alpha x^2 ) \cdot \cos (x^2 )}}<br />{{\sin (x^2 )}} \cdot \frac{{\tfrac{1}<br />{{x^2 }}}}<br />{{\tfrac{1}<br />{{x^2 }}}}} \right) \hfill \\<br /> \Leftrightarrow \mathop {\lim }\limits_{x \to 0^ - } \left( {\frac{{\frac{{\sin (\alpha x^2 ) \cdot \cos (x^2 )}}<br />{{x^2 }} \cdot \frac{\alpha }<br />{\alpha }}}<br />{{\frac{{\sin (x^2 )}}<br />{{x^2 }}}}} \right) = \mathop {\lim }\limits_{x \to 0^ - } \left( {\frac{{\overbrace {\frac{{\alpha \sin (\alpha x^2 )}}<br />{{\alpha x^2 }}}^{ \to \alpha } \cdot \overbrace {\cos (x^2 )}^{ \to 1}}}<br />{{\underbrace {\frac{{\sin (x^2 )}}<br />{{x^2 }}}_{ \to 1}}}} \right) = \alpha \hfill \\<br /> {\text{Veamos ahora el limite por la derecha:}} \hfill \\<br /> \mathop {\lim }\limits_{x \to 0^ + } \left( {\underbrace {x^2 + \beta x}_{ \to 0} + \beta } \right) = \beta \hfill \\<br /> \hfill \\<br /> {\text{Como los limites laterales deben ser iguales para que la funcion sea continua}}{\text{, concluimos}} \hfill \\<br /> {\text{que }}\alpha = \beta . \hfill \\ <br />\end{gathered} <br />\]<br />$ Mensaje modificado por rock&mati el Jan 23 2009, 09:01 PM

rock&mati rock&mati Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 23 2009, 09:00 PM Publicado: #3
Dios Matemático Grupo: Usuario FMAT Mensajes: 316 Registrado: 2-May 08 Desde: a la &$€¬~#@ del mundo Miembro Nº: 21.900 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaqjEa<br />% qaaiaabcfacaqGYaGaaeOlaiaab2caaaaabaaabaGaaeikaiaabMga<br />% caqGPbGaaeykamaaxababaGaciiBaiaacMgacaGGTbaaleaacaWG4b<br />% GaeyOKH4Qaey4kaSIaeyOhIukabeaakmaalaaabaWaaeWaaeaacaWG<br />% 4bGaeyOeI0IaaGymaaGaayjkaiaawMcaamaaCaaaleqabaGaaG4maa<br />% aakiabgkHiTiaadIhadaahaaWcbeqaaiaaiodaaaaakeaadaGcaaqa<br />% amaakaaabaGaaGynaaWcbeaakiaadIhacqGHRaWkcaaIZaGaamiEam<br />% aaCaaaleqabaGaaGinaaaaaeqaaaaakiabg2da9maaxababaGaciiB<br />% aiaacMgacaGGTbaaleaacaWG4bGaeyOKH4Qaey4kaSIaeyOhIukabe<br />% aakmaalaaabaGaeyOeI0IaaG4maiaadIhadaahaaWcbeqaaiaaikda<br />% aaGccqGHRaWkcaaIZaGaamiEaiabgkHiTiaaigdaaeaadaGcaaqaai<br />% aadIhadaahaaWcbeqaaiaaisdaaaGcdaqadaqaamaalaaabaWaaOaa<br />% aeaacaaI1aaaleqaaaGcbaGaamiEamaaCaaaleqabaGaaG4maaaaaa<br />% GccqGHRaWkcaaIZaaacaGLOaGaayzkaaaaleqaaaaakiabg2da9maa<br />% xababaGaciiBaiaacMgacaGGTbaaleaacaWG4bGaeyOKH4Qaey4kaS<br />% IaeyOhIukabeaakmaalaaabaWaaqIaaeaacaWG4bWaaWbaaSqabeaa<br />% caaIYaaaaaaakmaabmaabaGaeyOeI0IaaG4maiabgUcaRmaayeaaba<br />% WaaSaaaeaacaaIZaaabaGaamiEaaaacqGHsisldaWcaaqaaiaaigda<br />% aeaacaWG4bWaaWbaaSqabeaacaaIYaaaaaaaaeaacqGHsgIRcaaIWa<br />% aakiaawEJ-aaGaayjkaiaawMcaaaqaamaaKiaabaGaamiEamaaCaaa<br />% leqabaGaaGOmaaaaaaGcdaGcaaqaamaayaaabaWaaSaaaeaadaGcaa<br />% qaaiaaiwdaaSqabaaakeaacaWG4bWaaWbaaSqabeaacaaIZaaaaaaa<br />% aeaacqGHsgIRcaaIWaaakiaawIJ-aiabgUcaRiaaiodaaSqabaaaaO<br />% Gaeyypa0ZaaSaaaeaacqGHsislcaaIZaaabaWaaOaaaeaacaaIZaaa<br />% leqaaaaakiabg2da9iabgkHiTmaakaaabaGaaG4maaWcbeaaaaaa!96F9!<br />\[<br />\begin{gathered}<br /> \boxed{{\text{P2}}{\text{. - }}} \hfill \\<br /> \hfill \\<br /> {\text{(ii)}}\mathop {\lim }\limits_{x \to + \infty } \frac{{\left( {x - 1} \right)^3 - x^3 }}<br />{{\sqrt {\sqrt 5 x + 3x^4 } }} = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 3x^2 + 3x - 1}}<br />{{\sqrt {x^4 \left( {\frac{{\sqrt 5 }}<br />{{x^3 }} + 3} \right)} }} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\left( { - 3 + \overbrace {\frac{3}<br />{x} - \frac{1}<br />{{x^2 }}}^{ \to 0}} \right)}}<br />{{\sqrt {\underbrace {\frac{{\sqrt 5 }}<br />{{x^3 }}}_{ \to 0} + 3} }} = \frac{{ - 3}}<br />{{\sqrt 3 }} = - \sqrt 3 \hfill \\ <br />\end{gathered} <br />\]<br />$

rock&mati rock&mati Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 23 2009, 09:04 PM Publicado: #4
Dios Matemático Grupo: Usuario FMAT Mensajes: 316 Registrado: 2-May 08 Desde: a la &$€¬~#@ del mundo Miembro Nº: 21.900 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaqjEa<br />% qaaiaabcfacaqGYaGaaeOlaiaab2caaaaabaaabaGaaeikaiaabMga<br />% caqGPaWaaCbeaeaaciGGSbGaaiyAaiaac2gaaSqaaiaad6gacqGHsg<br />% IRcqGHEisPaeqaaOWaaOaaaeaadaWcaaqaaiaadwgadaahaaWcbeqa<br />% amaabmaabaWaaSqaaWqaaiaaigdaaeaacaWGUbaaaaWccaGLOaGaay<br />% zkaaWaaWbaaWqabeaacaaIYaaaaaaakiabgkHiTiaaigdaaeaadaqa<br />% daqaamaaleaaleaacaaIXaaabaGaamOBaaaaaOGaayjkaiaawMcaam<br />% aaCaaaleqabaGaaGOmaaaaaaaabeaakiaabccacaqGGaGaaeiiaiaa<br />% bccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGZbGaae<br />% yzaiaabggacaqGGaGaamyDaiabg2da9maabmaabaWaaSqaaSqaaiaa<br />% igdaaeaacaWGUbaaaaGccaGLOaGaayzkaaWaaWbaaSqabeaacaaIYa<br />% aaaOGaai4oaiaad6gacqGHsgIRcqGHEisPcaGG7aGaamyDaiabgkzi<br />% UkaaicdacaGGSaGaaeiiaiaabggacaqGSbGaaeiiaiaabkhacaqGLb<br />% GaaeyzaiaabohacaqGJbGaaeOCaiaabMgacaqGIbGaaeyAaiaabkha<br />% caqGGaGaaeyzaiaabYgacaqGGaGaaeiBaiaabMgacaqGTbGaaeyAai<br />% aabshacaqGLbGaaeiiaiaabshacaqGLbGaaeOBaiaabwgacaqGTbGa<br />% ae4BaiaabohacaqG6aaabaWaaCbeaeaaciGGSbGaaiyAaiaac2gaaS<br />% qaaiaadwhacqGHsgIRcaaIWaaabeaakmaakaaabaWaaSaaaeaacaWG<br />% LbWaaWbaaSqabeaacaWG1baaaOGaeyOeI0IaaGymaaqaaiaadwhaaa<br />% aaleqaaOGaeyypa0ZaaOaaaeaadaWfqaqaaiGacYgacaGGPbGaaiyB<br />% aaWcbaGaamyDaiabgkziUkaaicdaaeqaaOWaaSaaaeaacaWGLbWaaW<br />% baaSqabeaacaWG1baaaOGaeyOeI0IaaGymaaqaaiaadwhaaaaaleqa<br />% aOGaeyypa0JaaGymaaaaaa!9F99!<br />\[<br />\begin{gathered}<br /> \boxed{{\text{P2}}{\text{. - }}} \hfill \\<br /> \hfill \\<br /> {\text{(i)}}\mathop {\lim }\limits_{n \to \infty } \sqrt {\frac{{e^{\left( {\tfrac{1}<br />{n}} \right)^2 } - 1}}<br />{{\left( {\tfrac{1}<br />{n}} \right)^2 }}} {\text{ sea }}u = \left( {\tfrac{1}<br />{n}} \right)^2 ;n \to \infty ;u \to 0,{\text{ al reescribir el limite tenemos:}} \hfill \\<br /> \mathop {\lim }\limits_{u \to 0} \sqrt {\frac{{e^u - 1}}<br />{u}} = \sqrt {\mathop {\lim }\limits_{u \to 0} \frac{{e^u - 1}}<br />{u}} = 1 \hfill \\ <br />\end{gathered} <br />\]<br />$

snw Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 23 2009, 09:11 PM Publicado: #5
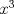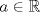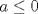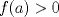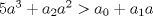Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	para el 2B) bastaria factorizar $TEX: $x^3$$ y aplicar el límite Del mismo modo se puede concluir que existe $TEX: $a\in{\Bbb R}$$ , particular si $TEX: $a\le 0$$ , de modo que $TEX: $f(a)>0$$ si y solo si $TEX: $5a^3+a_2a^2>a_0+a_1a$$ . 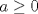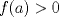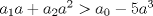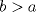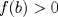Si $TEX: $a\ge 0$$ entonces $TEX: $f(a)>0$$ si y solo si $TEX: $a_1a+a_2a^2>a_0-5a^3$$ , pero si se cumple eso entonces para todo $TEX: $b>a$$ se cumplira que $TEX: $f(b)>0$$ . 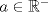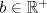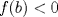Por lo tanto sólo para $TEX: $a\in{\Bbb R^-}$$ se satisface la condicion y en particular $TEX: $b\in{\Bbb R^+}$$ para cumplirse que $TEX: $f(b)<0$$ Mensaje modificado por snw el Jan 23 2009, 09:30 PM -------------------- blep

rock&mati rock&mati Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 23 2009, 09:13 PM Publicado: #6
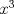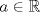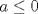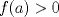Dios Matemático Grupo: Usuario FMAT Mensajes: 316 Registrado: 2-May 08 Desde: a la &$€¬~#@ del mundo Miembro Nº: 21.900 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(snw @ Jan 23 2009, 09:11 PM) para el 2B) bastaria factorizar $TEX: $x^3$$ y aplicar el límite Del mismo modo se puede concluir que existe $TEX: $a\in{\Bbb R}$$ , particular si $TEX: $a\le 0$$ , de modo que $TEX: $f(a)>0$$ si y solo si $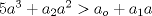TEX: $5a^3+a_2a^2>a_o+a_1a$$ . 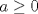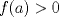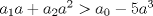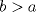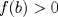Si $TEX: $a\ge 0$$ entonces $TEX: $f(a)>0$$ si y solo si $TEX: $a_1a+a_2a^2>a_0-5a^3$$ , pero si se cumple eso entonces para todo $TEX: $b>a$$ se cumplira que $TEX: $f(b)>0$$ . 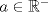Por lo tanto sólo para $TEX: $a\in{\Bbb R^-}$$ se satisface la condicion.

snw Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 23 2009, 09:19 PM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	para el P3: $TEX: Hay que notar que como $\{a_n\}$ es siemple creciente, entonces necesariamente es acotada, del mismo modo $\{b_n\}$ es decreciente y acotada para que se mantenga la desigualdad, en particular $\{a_n\}$ posee maximo y $\{b_n\}$minimo de modo que $\max\{a_n\}\le \min\{b_n\}$ conservando la desigualdad. Luego como existen maximos y minimos para $\{a_n\}$ y $\{b_n\}$ respectivamente, entonces coinciden con su supremo e infimo , probandose la desigualdad$ Mensaje modificado por snw el Jan 23 2009, 09:34 PM -------------------- blep

snw Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 23 2009, 09:41 PM Publicado: #8
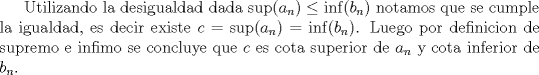Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: Utilizando la desigualdad dada $\sup(a_n)\le \inf(b_n)$ notamos que se cumple la igualdad, es decir existe $c=\sup(a_n)=\inf(b_n)$. Luego por definicion de supremo e infimo se concluye que $c$ es cota superior de $a_n$ y cota inferior de $b_n$.$ $TEX: Utilizando lo anterior, notemos que como $\{a_n\}$ y $\{b_n\}$ convergen a su supremo e infimo respectivamente, entonces se admite que $\displaystyle\lim_{n\to\infty}a_n-b_n=\lim_{n\to\infty}a_n-\lim_{n\to\infty}b_n=\sup(a_n)-\inf(b_n)=0$ si y solo si $\sup(a_n)=\inf(b_n)=c$ debido a la desigualdad anterior$ saludos (: Mensaje modificado por snw el Jan 23 2009, 09:52 PM -------------------- blep

rock&mati rock&mati Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 24 2009, 12:43 PM Publicado: #9
Dios Matemático Grupo: Usuario FMAT Mensajes: 316 Registrado: 2-May 08 Desde: a la &$€¬~#@ del mundo Miembro Nº: 21.900 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaqjEa<br />% qaaiaabcfacaqGXaGaaeOlaiaab2cacaqGbbaaaaqaaiaabseacaqG<br />% VbGaaeyBaiaabMgacaqGUbGaaeyAaiaab+gacaqG6aGaaeiiaiaabc<br />% cacaqGWbGaaeyyaiaabkhacaqGHbGaaeiiaiaabghacaqG1bGaaeyz<br />% aiaabccacaqGSbGaaeyyaiaabccacaqGMbGaaeyDaiaab6gacaqGJb<br />% GaaeyAaiaab+gacaqGUbGaaeiiaiaabwgacaqGZbGaaeiDaiaabwga<br />% caqGGaGaaeizaiaabwgacaqGMbGaaeyAaiaab6gacaqGPbGaaeizai<br />% aabggacaqGSaGaaeiiaiaabohacaqG1bGaaeiiaiaabsgacaqGLbGa<br />% aeOBaiaab+gacaqGTbGaaeyAaiaab6gacaqGHbGaaeizaiaab+gaca<br />% qGYbGaaeiiaiaabsgacaqGLbGaaeOyaiaabwgacaqGGaGaae4Caiaa<br />% bwgacaqGYbGaaeiiaiaabsgacaqGPbGaae4CaiaabshacaqGPbGaae<br />% OBaiaabshacaqGVbGaaeiiaiaabsgacaqGLbGaaeiiaiaabcdacaqG<br />% SaaabaGaaeiCaiaab+gacaqGYbGaaeiiaiaabYgacaqGVbGaaeiiai<br />% aabghacaqG1bGaaeyzaiaabccacaqGLbGaaeiBaiaabccacaqGKbGa<br />% ae4Baiaab2gacaqGPbGaaeOBaiaabMgacaqGVbGaaeiiaiaabsgaca<br />% qGLbGaaeiiaiaabYgacaqGHbGaaeiiaiaabAgacaqG1bGaaeOBaiaa<br />% bogacaqGPbGaae4Baiaab6gacaqGGaGaae4Caiaab+gacaqGUbGaae<br />% iiaiaabYgacaqGVbGaae4CaiaabccacqWIDesOcqGHsisldaGadaqa<br />% aiaaigdaaiaawUhacaGL9baaaeaaaeaacaqGdbGaaeyzaiaabkhaca<br />% qGVbGaae4CaiaabQdacaqGGaGaaeiiaiaabkgacaqGHbGaae4Caiaa<br />% bshacaqGHbGaaeiiaiaabMgacaqGNbGaaeyDaiaabggacaqGSbGaae<br />% yyaiaabkhacaqGGaGaaeyzaiaabYgacaqGGaGaaeizaiaabwgacaqG<br />% UbGaae4Baiaab2gacaqGPbGaaeOBaiaabggacaqGKbGaae4Baiaabk<br />% hacaqGGaGaaeyyaiaabccacaqGWaGaaeiiaiaabchacaqGHbGaaeOC<br />% aiaabggacaqGGaGaae4BaiaabkgacaqG0bGaaeyzaiaab6gacaqGLb<br />% GaaeOCaiaabccacaqGSbGaaeyyaiaabohacaqGGaGaaeOCaiaabgga<br />% caqGPbGaae4yaiaabwgacaqGZbGaaeilaiaabccacaWG4bGaey4kaS<br />% IaaGymaiabg2da9iaaicdacaGGSaGaaeiiaiaabsgacaqGVbGaaeOB<br />% aiaabsgacaqGLbGaaeiiaiaabYgacaqGHbGaae4Caaqaaiaabohaca<br />% qGVbGaaeiBaiaabwhacaqGJbGaaeyAaiaab+gacaqGUbGaaeyzaiaa<br />% bohacaqGGaGaae4Caiaab+gacaqGUbGaaeOoaiaabccacaWG4bWaaS<br />% baaSqaaiaaicdaaeqaaOGaeyypa0ZaaiWaaeaacqGHsislcaaIXaaa<br />% caGL7bGaayzFaaGaaiOlaaqaaaqaaiaabgeacaqGZbGaaeyAaiaab6<br />% gacaqG0bGaae4BaiaabshacaqGHbGaae4CaiaabQdaaeaacaqGQaGa<br />% aeisaiaab+gacaqGYbGaaeyAaiaabQhacaqGVbGaaeOBaiaabshaca<br />% qGHbGaaeiBaiaabwgacaqGZbGaaeOoaaqaamaaxababaGaciiBaiaa<br />% cMgacaGGTbaaleaacaWG4bGaeyOKH4Qaey4kaSIaeyOhIukabeaakm<br />% aabmaabaWaaSaaaeaacaWG4bGaey4kaSIaaGymaaqaaiaadIhacqGH<br />% sislcaaIXaaaaaGaayjkaiaawMcaaiabg2da9maaxababaGaciiBai<br />% aacMgacaGGTbaaleaacaWG4bGaeyOKH4Qaey4kaSIaeyOhIukabeaa<br />% kmaabmaabaWaaSaaaeaadaagbaqaaiaaigdacqGHRaWkdaWcbaWcba<br />% GaaGymaaqaaiaadIhaaaaabaGaeyOKH4QaaGymaaGccaGL34paaeaa<br />% daagaaqaaiaaigdacqGHsisldaWcbaWcbaGaaGymaaqaaiaadIhaaa<br />% aabaGaeyOKH4QaaGymaaGccaGL44paaaaacaGLOaGaayzkaaGaeyyp<br />% a0ZaauIhaeaadaqjuaqaaiaaigdaaaaaaaqaamaaxababaGaciiBai<br />% aacMgacaGGTbaaleaacaWG4bGaeyOKH4QaeyOeI0IaeyOhIukabeaa<br />% kmaabmaabaWaaSaaaeaacaWG4bGaey4kaSIaaGymaaqaaiaadIhacq<br />% GHsislcaaIXaaaaaGaayjkaiaawMcaaiabg2da9maaxababaGaciiB<br />% aiaacMgacaGGTbaaleaacaWG4bGaeyOKH4QaeyOeI0IaeyOhIukabe<br />% aakmaabmaabaWaaSaaaeaadaagbaqaaiaaigdacqGHRaWkdaWcbaWc<br />% baGaaGymaaqaaiaadIhaaaaabaGaeyOKH4QaaGymaaGccaGL34paae<br />% aadaagaaqaaiaaigdacqGHsisldaWcbaWcbaGaaGymaaqaaiaadIha<br />% aaaabaGaeyOKH4QaaGymaaGccaGL44paaaaacaGLOaGaayzkaaGaey<br />% ypa0ZaauIhaeaadaqjuaqaaiaaigdaaaaaaaqaaiaabQcacaqGwbGa<br />% aeyzaiaabkhacaqG0bGaaeyAaiaabogacaqGHbGaaeiBaiaabwgaca<br />% qGZbGaaeOoaiaabccacaqGqbGaae4BaiaabohacaqGPbGaaeOyaiaa<br />% bYgacaqGLbGaaeiiaiaabogacaqGHbGaaeOBaiaabsgacaqGPbGaae<br />% izaiaabggacaqG0bGaae4BaiaabccacaWG4bGaeyypa0JaaGymaaqa<br />% amaaxababaGaciiBaiaacMgacaGGTbaaleaacaWG4bGaeyOKH4QaaG<br />% ymaaqabaGcdaqadaqaamaalaaabaWaaGraaeaacaWG4bGaey4kaSIa<br />% aGymaaWcbaGaeyOKH4QaaGOmaaGccaGL34paaeaadaagaaqaaiaadI<br />% hacqGHsislcaaIXaaaleaacaaIWaaakiaawIJ-aaaaaiaawIcacaGL<br />% PaaacqGH9aqpcqGHEisPaeaacaGGQaGaae4taiaabkgacaqGSbGaae<br />% yAaiaabogacaqG1bGaaeyyaiaabohacaqG6aaabaWaaCbeaeaaciGG<br />% SbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHRaWkcqGHEisPae<br />% qaaOWaaeWaaeaadaWcaaqaaiaadIhacqGHRaWkcaaIXaaabaGaamiE<br />% amaabmaabaGaamiEaiabgkHiTiaaigdaaiaawIcacaGLPaaaaaaaca<br />% GLOaGaayzkaaGaeyypa0JaaGimaaqaaiaabcfacaqGVbGaaeOCaiaa<br />% bccacaqGSbGaae4BaiaabccacaqGXbGaaeyDaiaabwgacaqGGaGaae<br />% iBaiaabggacaqGZbGaaeiiaiaabggacaqGZbGaaeyAaiaab6gacaqG<br />% 0bGaae4BaiaabshacaqGHbGaae4CaiaabccacaqGZbGaae4Baiaab6<br />% gacaqG6aGaaeiiaiaadMhacqGH9aqpcaaIXaGaai4oaiaadIhacqGH<br />% 9aqpcaaIXaGaaiOlaaaaaa!EAB3!<br />\[<br />\begin{gathered}<br /> \boxed{{\text{P1}}{\text{. - A}}} \hfill \\<br /> {\text{Dominio: para que la funcion este definida}}{\text{, su denominador debe ser distinto de 0}}{\text{,}} \hfill \\<br /> {\text{por lo que el dominio de la funcion son los }}\mathbb{R} - \left\{ 1 \right\} \hfill \\<br /> \hfill \\<br /> {\text{Ceros: basta igualar el denominador a 0 para obtener las raices}}{\text{, }}x + 1 = 0,{\text{ donde las}} \hfill \\<br /> {\text{soluciones son: }}x_0 = \left\{ { - 1} \right\}. \hfill \\<br /> \hfill \\<br /> {\text{Asintotas:}} \hfill \\<br /> {\text{Horizontales:}} \hfill \\<br /> \mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{x + 1}}<br />{{x - 1}}} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{\overbrace {1 + \tfrac{1}<br />{x}}^{ \to 1}}}<br />{{\underbrace {1 - \tfrac{1}<br />{x}}_{ \to 1}}}} \right) = \boxed{\left. {\underline {\, <br /> 1 \,}}\! \right\| } \hfill \\<br /> \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{x + 1}}<br />{{x - 1}}} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{\overbrace {1 + \tfrac{1}<br />{x}}^{ \to 1}}}<br />{{\underbrace {1 - \tfrac{1}<br />{x}}_{ \to 1}}}} \right) = \boxed{\left. {\underline {\, <br /> 1 \,}}\! \right\| } \hfill \\<br /> {\text{Verticales: Posible candidato }}x = 1 \hfill \\<br /> \mathop {\lim }\limits_{x \to 1} \left( {\frac{{\overbrace {x + 1}^{ \to 2}}}<br />{{\underbrace {x - 1}_0}}} \right) = \infty \hfill \\<br /> {\text{Oblicuas:}} \hfill \\<br /> \mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{x + 1}}<br />{{x\left( {x - 1} \right)}}} \right) = 0 \hfill \\<br /> {\text{Por lo que las asintotas son: }}y = 1;x = 1. \hfill \\ <br />\end{gathered} <br />\]<br />$ Archivo(s) Adjunto(s)* aasdasd.PNG ( 8.62k ) Número de descargas: 0

« Posterior · Matemáticas III · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 24th November 2024 - 02:34 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.