desigualdad - Foro fmat.cl

2 Páginas:

1 2 >

desigualdad, para los amigos:D

febomon Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 4 2009, 07:25 PM Publicado: #1
Dios Matemático Grupo: Usuario FMAT Mensajes: 448 Registrado: 27-January 08 Miembro Nº: 15.045 Nacionalidad: Sexo:	demustre que para todo n perteneciente a los naturales se cumple: 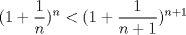$TEX: <br />$$<br />(1 + \frac{1}<br />{n})^n < (1 + \frac{1}<br />{{n + 1}})^{n + 1} <br />$$<br />$ espero una solucion sin calculo saludos Mensaje modificado por febomon el Jan 4 2009, 08:08 PM

7words Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 10 2009, 09:00 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.756 Registrado: 16-September 07 Desde: al frente del Express Miembro Nº: 10.238 Nacionalidad: Universidad: Sexo:	sorry si no es la respuesta qe esperabas $TEX: \[\left( {1 + \frac{1}{{n + 1}}} \right)^{n + 1} > \left( {1 + \frac{1}{n}} \right)^n ,\forall n \in \mathbb{N}\]$ $TEX: \[sea:a_1 = 1,a_2 = 1 + \frac{1}{2}......a_n = 1 + \frac{1}{n}\]$ $TEX: \[por\,MA > MG,\,tenemos\,que:\]$ $TEX: \[\frac{{\sum\limits_{k = 1}^{n + 1} {a_k } }}{{n + 1}} > \sqrt[{n + 1}]{{a_1 a_2 ...a_n }}\]$ $TEX: \[\Rightarrow \frac{{1 + n\left( {1 + \frac{1}{n}} \right)}}{{n + 1}} > \sqrt[{n + 1}]{{\left( {1 + \frac{1}{n}} \right)^n }}\]$ $TEX: \[ \Rightarrow \frac{{n + 2}}{{n + 1}} > \sqrt[{n + 1}]{{\left( {1 + \frac{1}{n}} \right)^n }}\]$ $TEX: \[ \Rightarrow 1 + \frac{1}{{n + 1}} > \sqrt[{n + 1}]{{\left( {1 + \frac{1}{n}} \right)^n }}/\left( . 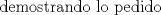\right)^{n + 1} \]$ $TEX: \[\Rightarrow \left( {1 + \frac{1}{{n + 1}}} \right)^{n + 1} > \left( {1 + \frac{1}{n}} \right)^n \]$ $TEX: demostrando lo pedido$ saludos!^^ -------------------- Ahora van quedando en el foro solo los niñitos tontitos graves, que lata... u.u

snw Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 10 2009, 09:14 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	disculpa la incredulidad ... pero no estoy seguro el porque 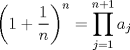$TEX: $\displaystyle\left(1+\frac{1}{n}\right)^n=\prod_{j=1}^{n+1}a_j$$ Mensaje modificado por snw el Jan 10 2009, 09:14 PM -------------------- blep

7words Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 10 2009, 09:34 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.756 Registrado: 16-September 07 Desde: al frente del Express Miembro Nº: 10.238 Nacionalidad: Universidad: Sexo:	CITA(snw @ Jan 10 2009, 11:14 PM) disculpa la incredulidad ... pero no estoy seguro el porque > cuek! buen detalle me equivoqe yo al escribirlo altiro edit -------------------- Ahora van quedando en el foro solo los niñitos tontitos graves, que lata... u.u

7words Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 10 2009, 09:39 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.756 Registrado: 16-September 07 Desde: al frente del Express Miembro Nº: 10.238 Nacionalidad: Universidad: Sexo:	CITA(7words @ Jan 10 2009, 11:00 PM) sorry si no es la respuesta qe esperabas $TEX: \[\left( {1 + \frac{1}{{n + 1}}} \right)^{n + 1} > \left( {1 + \frac{1}{n}} \right)^n ,\forall n \in \mathbb{N}\]$ $TEX: \[por\,MA > MG,\,tenemos\,que:\]$ $TEX: \[sea:a_1 = 1,a_2 = 1 + \frac{1}{2}......a_n = 1 + \frac{1}{n}\]$ $TEX: \[\frac{{\sum\limits_{k = 1}^{n + 1} {a_k } }}{{n + 1}} > \sqrt[{n + 1}]{{a_1 a_2 ...a_{n + 1} }}\]$ $TEX: \[ \Rightarrow \frac{{1 + n\left( {1 + \frac{1}{n}} \right)}}{{n + 1}} > \sqrt[{n + 1}]{{\left( {1 + \frac{1}{n}} \right)^n }}\]$ $TEX: \[\Rightarrow \frac{{n + 2}}{{n + 1}} > \sqrt[{n + 1}]{{\left( {1 + \frac{1}{n}} \right)^n }}\]$ $TEX: \[\Rightarrow 1 + \frac{1}{{n + 1}} > \sqrt[{n + 1}]{{\left( {1 + \frac{1}{n}} \right)^n }}/\left( . \right)^{n + 1} \]$ $TEX: \[\Rightarrow \left( {1 + \frac{1}{{n + 1}}} \right)^{n + 1} > \left( {1 + \frac{1}{n}} \right)^n \]$ saludos!^^ -------------------- Ahora van quedando en el foro solo los niñitos tontitos graves, que lata... u.u

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 10 2009, 09:52 PM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Yo creo que se refiere a que $TEX: \[\frac{1+\overbrace{\left(1+\frac{1}{n}\right)+\ldots+\left(1+\frac{1}{n}\right)}^{n\text{ veces}}}{n+1}\geq \sqrt[n+1]{1\cdot \left(1+\frac{1}{n}\right)^n}\]$ ? -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

snw Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 10 2009, 10:08 PM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Abu-Khalil @ Jan 10 2009, 11:52 PM) Yo creo que se refiere a que $TEX: \[\frac{1+\overbrace{\left(1+\frac{1}{n}\right)+\ldots+\left(1+\frac{1}{n}\right)}^{n\text{ veces}}}{n+1}\geq \sqrt[n+1]{1\cdot \left(1+\frac{1}{n}\right)^n}\]$ ? si es asi, buena solucion yo lo miré el otro dia y no se me ocurrio nada xd -------------------- blep

febomon Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 14 2009, 06:54 PM Publicado: #8
Dios Matemático Grupo: Usuario FMAT Mensajes: 448 Registrado: 27-January 08 Miembro Nº: 15.045 Nacionalidad: Sexo:	muy bien 7 words esta correcta

febomon Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 14 2009, 06:55 PM Publicado: #9
Dios Matemático Grupo: Usuario FMAT Mensajes: 448 Registrado: 27-January 08 Miembro Nº: 15.045 Nacionalidad: Sexo:	CITA(Abu-Khalil @ Jan 11 2009, 12:22 PM) Yo creo que se refiere a que $TEX: \[\frac{1+\overbrace{\left(1+\frac{1}{n}\right)+\ldots+\left(1+\frac{1}{n}\right)}^{n\text{ veces}}}{n+1}\geq \sqrt[n+1]{1\cdot \left(1+\frac{1}{n}\right)^n}\]$ ? ese era el truco maligno xd

Naxoo Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 23 2009, 07:57 PM Publicado: #10
Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Esta desigualdad la intente sacar como 2 dias y no salio xD entonces averigue un poco y existen, aparte de esta, unas 2 soluciones mas, bastante ingeniosas, a ver si alguien las encuentra o saca otras -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti $TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />$

2 Páginas:

1 2 >

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 23rd November 2024 - 11:33 PM