1ª Killer Maraton - Foro fmat.cl

1ª Killer Maraton, Solo para valientes

Cesarator	Aug 12 2006, 09:47 PM Publicado: #91
Invitado	Damos inicio entonces a nuestra primera GRAN KILLER MARATON. Para tener derecho a postear aqui, primero hay que inscribirse y leer las reglas: Reglamento e inscripciones Esta es una competicion oficial FMAT, y se premiara a los ganadores. Y como sospecho que esto nos dara un largo tiempo de diversion, comencemos de inmediato. Recuerdo que la dificultad sera variada: problemas dificiles, tambien algunos relativamente simples. No se hara ningun comentario sobre la dificultad de cada problema hasta despues de resuelto. GO! $TEX: <br />{\bf Problema 1}. Sean $x,y,z>0$ tales que $\displaystyle \frac{1}{x^2} + \frac{1}{y^2}+ \frac{1}{z^2} =1$. Demostrar la desigualdad<br />\[<br />\frac{xy}{xy-1} + \frac{yz}{yz-1} + \frac{zx}{zx-1} \le \frac{9}{2}.<br />\]<br />$

Respuestas

Pasten Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 23 2007, 12:40 AM Publicado: #92
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad: Sexo:	$TEX: \noindent<br />Por comodidad diremos que un grupo conectado es un grupo bueno, en caso contrario es un grupo malo. Un tunel de un solo sentido entre $A$ y $B$ sera una "flecha" y lo denotamos $AB$, en ese orden. Al hablar de "grupo" entiendase un conjunto de $4$ estaciones dadas, en caso contrario se especificara como conjunto indicando cuantas estaciones estan.\\<br />Dado un grupo, una estacion es de entrada si a ella llegan $3$ flechas y es de salida si de ella salen $3$ flechas, en ambos casos diremos que la estacion es fea.\\<br />Resolveremos el problema para $2n+3$ estaciones, con $n\ge3$ (o sea, para los impares mayores que $8$), por lo que en adelante asuma que esa es la cantidad de estaciones.<br />$ $TEX: \noindent<br />Caractericemos los grupos malos:\\<br />Lema 1: Un grupo es malo ssi tiene una estacion fea.\\<br />Demostracion: Si tiene una estacion fea es obvio que es malo (si es de salida no se puede llegar a ella, si es de entrada no se puede salir de ella).\\<br />Supongamos que no tiene estaciones feas y que las estaciones del grupo son $A,B,C,D$. Tratemos de forzar que el grupo sea malo sin estaciones feas. Si un tunel es doble complicamos el asunto remplazandolo por una flecha asi que digamos que no hay tuneles dobles. Sin perder generalidad asuma que ya estan las flechas $AB,AC,DA$, hay dos casos:\\<br />i) Esta la flecha BC: entonces esta la CD y el grupo es bueno. No sirve\\<br />ii) Esta la flecha CB: entonces esta la BD y el grupo es bueno. Tampoco sirve\\<br />Como cualquier otro caso nos lleva a un grafo dirigido isomorfo (salvo quisas el sentido de todas las flechas simultaneamente) vemos que no se puede, probando el lema. 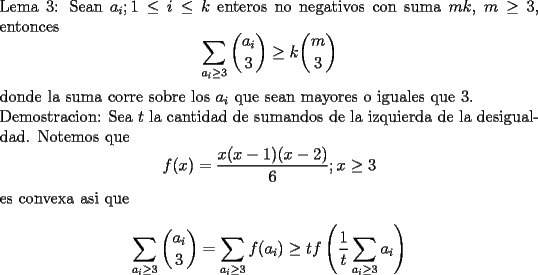\\<br />\\<br />Lema 2: Cada grupo tiene a lo mas una estacion de salida.\\<br />Demostracion: Un grupo tiene a lo mas $2$ estaciones feas (trivial), que seran necesariamente una de entrada y otra de salida, por lo cual cada grupo tiene a lo mas una estacion de salida.\\<br />$ $TEX: \noindent<br />Lema 3: Sean $a_i;1\le i\le k$ enteros no negativos con suma $mk$, $m\ge3$, entonces<br />$$\sum_{a_i\ge 3}\binom{a_i}{3}\ge k\binom{m}{3}$$<br />donde la suma corre sobre los $a_i$ que sean mayores o iguales que $3$.\\<br />Demostracion: Sea $t$ la cantidad de sumandos de la izquierda de la desigualdad. 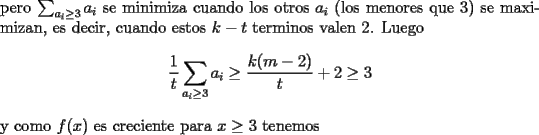Notemos que <br />$$f(x)=\frac{x(x-1)(x-2)}{6}; x\ge 3$$<br />es convexa asi que<br />$$\sum_{a_i\ge 3}\binom{a_i}{3}=\sum_{a_i\ge 3}f(a_i)\ge tf\left(\frac{1}{t}\sum_{a_i\ge3}a_i\right)$$<br />$ $TEX: \noindent<br />pero $\sum_{a_i\ge 3}a_i$ se minimiza cuando los otros $a_i$ (los menores que $3$) se maximizan, es decir, cuando estos $k-t$ terminos valen $2$. 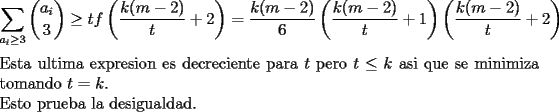Luego<br />$$\frac{1}{t}\sum_{a_i\ge3}a_i\ge \frac{k(m-2)}{t}+2\ge 3$$<br />y como $f(x)$ es creciente para $x\ge 3$ tenemos<br />$ $TEX: \noindent<br />$$\sum_{a_i\ge 3}\binom{a_i}{3}\ge tf\left(\frac{k(m-2)}{t}+2\right) =\frac{k(m-2)}{6}\left(\frac{k(m-2)}{t}+1\right)\left(\frac{k(m-2)}{t}+2\right)$$<br />Esta ultima expresion es decreciente para $t$ pero $t\le k$ asi que se minimiza tomando $t=k$.\\<br />Esto prueba la desigualdad.<br />$ $TEX: \noindent<br />Ya con estos $3$ lemas podemos continuar;\\<br />En total hay $\frac{(2n+3)(2n+2)}{2}-(2n+3)=n(2n+3)$ flechas.\\<br />Luego, si a cada estacion le asignamos uno de los numeros $s_i:1\le i\le 2n+3$ que en cada caso correspondera a la cantidad de flechas que salen de esa estacion (la estacion i-esima), vemos que $\sum s_i=n(2n+3)$.<br />Si por cada grupo posible contamos la cantidad de estaciones de salida (cada estacion puede ser contada tantas veces como grupos en los que figure como estacion de salida) vemos que este numero (que llamaremos $\sigma$) es<br />$$\sum_{s_i\ge 3}\binom{s_i}{3}$$<br />porque solo pueden considerarse estaciones de las que salen al menos $3$ flechas, y la estacion $i$-esima aparecera contada en $\binom{s_i}{3}$ grupos.\\<br />Aplicamos el Lema 3, tomando $k=2n+3,m=n,a_i=s_i$ y obtenemos <br />$$\sigma\ge (2n+3)\binom{n}{3}$$<br />Ahora de los lemas 1 y 2 se sigue que el total de grupos malos no puede ser inferior a $\sigma$, desigualdad que resulta ser bastante bruta porque ni siquiera consideramos las de llegada.<br />$ $TEX: \noindent<br />Tomemos las estaciones como vertices de un poligono regular de $2n+3$ lados y numeradas desde 1 en sentido antihorario. Los lados del poligono seran los tuneles dobles. Las diagonales seran flechas con sentido antihorario respecto del centro del poligono si en el semiplano determinado por esa diagonal y que no contiene el centro hay una cantidad impar de vertices. En otro caso la flecha va en sentido horario respecto del centro.\\<br />Si un grupo contiene estaciones consecutivas no es complicado ver que es bueno, asi que los grupos malos no tienen estaciones consecutivas y solo estan conectados por flechas.\\<br />Miremos la estacion 1. De ella salen $n$ flechas y llegan $n$. Luego, sera estacion de salida en $\binom{n}{3}$ grupos y sera de llegada en otros $\binom{n}{3}$.<br />$ $TEX: \noindent<br />Si miramos alguno de los grupos en los que es estacion de salida, por los sentidos de las flechas que dimos no es complicado ver (por paridad) que la primera estacion del grupo que nos encontramos al recorrer en sentido horario los vertices del poligono desde la estacion 1, es una estacion de llegada para el grupo (que llamaremos $L$). Esto porque todas las flechas del grupo que no tocan a la estacion 1 van en sentido antihorario respecto de dicha estacion.\\<br />En efecto, las flechas que salen de la estacion 1 llegan a las estaciones de numeracion impar (salvo la $2n+3$ que es contigua). Esto es trivial para las de numeracion impar menor que $\frac{1}{2}(2n+3)$ pues son flechas en sentido antihorario, para las otras como son en sentido horario pero ya pasaron de la mitad del poligono estaran ditigidas a la estacion 1. Ahora a la $L$ llega una flecha desde la estacion 1, pero las demas del grupo tienen igual paridad que esta estacion asi que, con un razonamiento similar al anterior, vemos que las flechas del grupo que tocan $L$ se dirigen a ella.$ $TEX: \noindent<br />Por lo tanto en cada grupo donde la estacion 1 sea de salida, habra otra estacion de llegada. Ocurre de forma similar para los grupos en los que la estacion 1 es de llegada, estos tendran necesariamente una estacion de salida. Asi del lema 2 vemos que cada vez que la estacion 1 es fea, contamos un grupo malo pero cada uno de estos grupos tiene otra estacion fea asi que al repetir el proceso con las demas estaciones, cada grupo malo sera contado 2 veces. 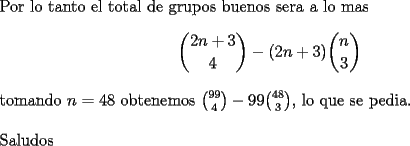A demas esto es para todos los grupos malos, por el lema 1.\\<br />Como la numeracion de las estaciones fue arbitraria, esto ocurre con las $2n+3$ estaciones.\\<br />Luego, esta configuracion nos da <br />$$\frac{1}{2}(2n+3)\left(\binom{n}{3}+\binom{n}{3}\right)=(2n+3)\binom{n}{3}$$<br />grupos malos, que es el minimo posible<br />$ $TEX: \noindent<br />Por lo tanto el total de grupos buenos sera a lo mas<br />$$\binom{2n+3}{4}-(2n+3)\binom{n}{3}$$<br />tomando $n=48$ obtenemos $\binom{99}{4}-99\binom{48}{3}$, lo que se pedia.\\<br />\\<br />Saludos<br />$ -------------------- Pasten, un buen muchacho en quien confiar.

Mensajes en este tema

Cesarator 1ª Killer Maraton Aug 12 2006, 09:47 PM

Guía Rojo Utilicemos el cambio de variable $\left... Aug 19 2006, 12:52 AM

Cesarator Solución habemus. Impecable y merecedora de los ... Aug 19 2006, 08:28 AM

Cesarator {\bf Problema 2}. Sea $M$ un punto... Aug 19 2006, 08:34 AM

†Alucard† Se usará $(\triangle{N})$ para deno... Aug 19 2006, 09:09 AM

Pasten http://img92.imageshack.us/... Aug 19 2006, 01:57 PM

Cesarator doy el p2 por resuelto, la revision en detalle y a... Aug 19 2006, 09:17 PM

Pasten \noindent Consideremos una tabla con ... Aug 20 2006, 11:29 AM

†Alucard† Sabemos que cada alumno tiene dos abuelos (materno... Aug 19 2006, 09:36 PM

Cesarator Resuelto el P3. Nuevamente dejamos pendiente la re... Aug 19 2006, 09:51 PM

†Alucard† Se me adelantaron... Bueno, por lo menos puedo ... Aug 20 2006, 12:20 PM

Killua Solución: \noindent Notamos que sacando las ... Aug 19 2006, 10:40 PM

Cesarator nop, a veces el apuro nos hace equivocarnos en cos... Aug 19 2006, 10:51 PM

Killua Creo que me precipité demasiado.... $\b... Aug 19 2006, 11:21 PM

Pasten http://img209.imageshack... Aug 20 2006, 03:22 AM

Cesarator wow! excelente! no tienen piedad con este ... Aug 20 2006, 01:33 PM

zirou Si $c_n$ contiene n ceros en su escritur... Aug 20 2006, 02:47 PM

Kenshin Porque afirmas esto? :dunno: :dunno: Saludos ... Aug 20 2006, 02:59 PM

†Alucard† Primero fijemos trabajaremos sólo con los números ... Aug 20 2006, 03:01 PM

Cesarator Bien! el p4 es de una olimpiada internacional ... Aug 20 2006, 04:12 PM

zirou Recordemos que la paridad solo da cupo a dos opcio... Aug 20 2006, 04:26 PM

Pasten \noindent Para el caso, como lo que nos inter... Aug 20 2006, 05:29 PM

Ivan Acrata Veamos el caso de 100 números consecutivos ... Aug 20 2006, 09:31 PM

Cesarator \noindent {\bf Problema 7}. Determinar ... Aug 20 2006, 10:34 PM

†Alucard† Primero notamos que, para un $x\in... Aug 20 2006, 11:11 PM

Cesarator {\bf Problema 8}. Sea $n>1$ un ... Aug 22 2006, 11:16 AM

Pasten \noindent Llamemos $P(x)$ al pol... Aug 22 2006, 11:31 PM

Ivan Acrata Sea ( \[ \alpha ,\beta \] ) lo... Aug 22 2006, 11:29 PM

Cesarator Perdon por el abandono, ya vendran tiempos con mas... Aug 24 2006, 09:08 PM

†Alucard† Se llamará descomposición válida de x a una conjun... Aug 24 2006, 10:02 PM

Cesarator {\bf Problema 10}. Sean $p,q,r,s$ ... Aug 24 2006, 10:17 PM

†Alucard† Sea $P=(p-q)(p-r)(p-s)(q-r)(q-s)(r-s)$ ... Aug 24 2006, 10:30 PM

Cesarator {\bf Problema 11}. Encontrar todas las soluc... Aug 28 2006, 02:19 PM

Pasten \noindent Tomemos las funciones\\ ... Aug 28 2006, 03:02 PM

Cesarator mmm, no puedo dar por resuelto el P11. El calculo ... Aug 28 2006, 05:17 PM

Luffy Si $x\ge0 \Rightarrow 3^x>2^x... Aug 28 2006, 05:17 PM

Cesarator ... lo mismo. Correcta pero NO. Me conformo con ve... Aug 28 2006, 05:22 PM

Luffy si $x$ es natural: $2^1>1... Aug 28 2006, 05:36 PM

Cesarator {\bf Problema 12}. Sean $p_1, ..., p_k... Aug 28 2006, 06:10 PM

Ivan Acrata Para i...., pertenece a algún conjunto en especial... Aug 30 2006, 09:39 PM

Cesarator ... aprovecho de recordar que no se responden preg... Aug 30 2006, 09:47 PM

Caetano \noindent Sea $S_j=\displaystyle... Sep 3 2006, 06:37 PM

Cesarator ... no se entiende lo que es $P_m$ ¿Erro... Sep 4 2006, 06:28 PM

Caetano Por ejemplo, para $k=3$ tendriamos que: ... Sep 4 2006, 06:43 PM

Cesarator ahora entiendo a lo que te refieres, pero esta mal... Sep 4 2006, 07:05 PM

Caetano Editado Sep 4 2006, 07:28 PM

Guía Rojo ahora soy yo el que no entiende muy bien... cómo s... Sep 4 2006, 09:41 PM

Luffy seria asi: $P_1=p_1+p_2+p_3+p_4$ ... Sep 4 2006, 09:49 PM

Guía Rojo bien, gracias... con eso me aclaraste la última d... Sep 6 2006, 09:56 PM

Cesarator ... leve mejora, pero sigue estando mal escrito... Sep 5 2006, 08:46 AM

Cesarator {\bf Problema 12}. Sean $p_1, ..., p_k... Sep 11 2006, 11:07 AM

Cesarator .. que bueno que han tenido piedad por este pobre ... Oct 6 2006, 09:38 AM

Caetano Ya que me titaron un palo por ahi, posteo pero sin... Oct 17 2006, 10:05 PM

Cesarator bueno, y como se demuestra esta identidad con la... Oct 18 2006, 01:36 PM

Cesarator \[ \sum_{simetrica} ??????? \] Oct 17 2006, 10:46 PM

Luffy $\displaystyle\sum_{simetrica}f(x,y... Oct 17 2006, 11:37 PM

Cesarator {\bf Problema 13}. Sea $ABCD$ un cu... Oct 20 2006, 03:20 PM

Pasten Bien... como no pude encontrar una mejor solucion,... Oct 20 2006, 06:18 PM

†Alucard† Todos los ángulos expresados estarán en grados, au... Oct 20 2006, 07:12 PM

Cesarator {\bf Problema 14}. Sea $X=\{1,2,3... Oct 20 2006, 08:04 PM

Pasten \noindent Busquemos el subconjunto $A... Oct 21 2006, 10:59 AM

†Alucard† Sea $k\in\mathbb{N}$ fijo, con... Oct 20 2006, 08:34 PM

Cesarator Respuesta incorrecta Oct 20 2006, 10:25 PM

Cesarator {\bf Problema 15}. Sean $a,b,c>0... Oct 21 2006, 02:49 PM

Pasten \noindent Asuma $\sum$ como s... Oct 22 2006, 12:50 AM

Cesarator {\bf Problema 16}. Sean $M$ y ... Oct 22 2006, 12:53 PM

Pasten http://img342.imageshack.u... Oct 22 2006, 01:32 PM

Cesarator {\bf Problema 17}. Sea $k$ un ente... Oct 22 2006, 01:56 PM

Caetano \noindent Primero probaremos por induccion qu... Oct 22 2006, 03:09 PM

Cesarator {\bf Problema 18}. Sea $ABCD$ un c... Oct 22 2006, 03:58 PM

Pasten http://img335.imageshack.u... Oct 23 2006, 04:26 PM

Luffy $\boxed{P_{17}}$ $a_{n+1}=a_n... Oct 22 2006, 05:25 PM

Luffy Jajaja solo quiero aclarar un :condoro: que tu... Oct 28 2006, 11:05 PM

Caetano \noindent Sea ABCD el cuadrilatero de la figu... Oct 22 2006, 10:59 PM

Cesarator {\bf Problema 19}. Considerar dos tri\... Oct 23 2006, 08:45 AM

Pasten \noindent Sea $k:\frac{1}{2k}=... Oct 23 2006, 11:01 AM

Cesarator Ver punto 4b) del reglamento REGLAMENTO K-MARATON Oct 23 2006, 11:26 AM

Luffy Situemos $A'$ en $A$, lueg... Oct 23 2006, 02:29 PM

Caetano Problema 19 \noindent Sean $\alpha... Oct 23 2006, 06:25 PM

Cesarator {\bf Problema 20}. Sean $P, Q$ pun... Oct 23 2006, 06:28 PM

Caetano Pero la medida del $\angle BAC=60$ ... Oct 23 2006, 06:38 PM

Cesarator Gracias, problema corregido. {\bf Problema ... Oct 23 2006, 06:46 PM

Pasten listo... ver abajo el post Oct 24 2006, 12:09 PM

Pasten Construimos $X,Y$ sobre AB,AC de modo q... Oct 24 2006, 06:01 PM

Cesarator mmm, debe justificarse mejor el primer paso... Oct 24 2006, 12:36 PM

Pasten Ok, ya modifique el post (en todo caso es la mism... Oct 24 2006, 04:10 PM

Luffy Error de solución, por favor editar. Oct 24 2006, 04:11 PM

Cesarator ... el "primer paso" es la igualdad de l... Oct 24 2006, 04:53 PM

Cesarator {\bf Problema 21} Sean $A,B,C,D,E... Oct 24 2006, 06:31 PM

Pasten Si un cuadrilatero en el espacio es paralelogramo... Oct 24 2006, 07:24 PM

Cesarator chuuu, sorry, nuevo error de tipeo, confundi el ul... Oct 24 2006, 09:01 PM

Pasten http://img57.imageshack.us... Oct 24 2006, 09:47 PM

Cesarator Justificar + esta parte Oct 24 2006, 10:21 PM

Pasten Ok, ya esta Oct 24 2006, 11:40 PM

Cesarator {\bf Problema 22}. Demostrar que para cada e... Oct 25 2006, 07:43 AM

Pasten \noindent Se trabajara en enteros. Diremos q... Dec 11 2006, 01:51 PM

Cesarator :jpt_sleep: ... parece que me va a tomar su time ... Dec 12 2006, 09:13 AM

Pasten \noindent Diremos que un numero es "ga... Dec 12 2006, 08:10 PM

Cesarator ... solo decir que el problema anterior pertenece ... Dec 14 2006, 02:53 PM

Pasten \noindent Por comodidad diremos que un grupo ... Jul 23 2007, 12:40 AM

« Posterior · Problemas Propuestos · Anterior »

2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):