|
|
|
|
|
|
|
  |
 Oct 22 2006, 05:25 PM Oct 22 2006, 05:25 PM
Publicado:
#71
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
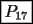 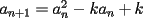 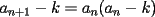 Luego, sea  ; digamos que ; digamos que 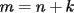 : :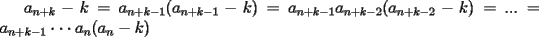 Luego: 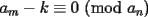 Luego como 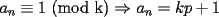 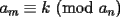 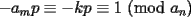 Finalmente 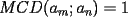
|
|
|
|
 Oct 22 2006, 10:59 PM Oct 22 2006, 10:59 PM
Publicado:
#72
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 293 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 3 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
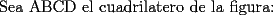  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img120.imageshack.us/img120/2264/convexoaa7.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img120.imageshack.us/img120/2264/convexoaa7.png');}" />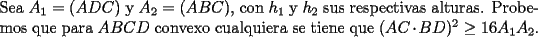 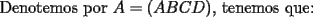 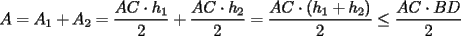 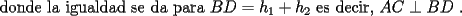 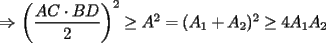 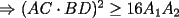 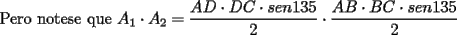 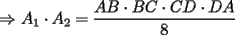 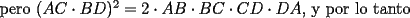 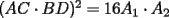 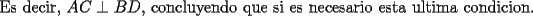
Mensaje modificado por Caetano el Oct 22 2006, 11:03 PM --------------------  |
|
|
|
| Cesarator |
 Oct 23 2006, 08:45 AM Oct 23 2006, 08:45 AM
Publicado:
#73
|
|
Invitado |
![TEX: <br />{\bf Problema 19}. Considerar dos tri\'angulos $\triangle ABC$ y $\triangle A'B'C'$ con<br />$\angle C \cong \angle C'$. Asumir que , adem\'as, <br />\[<br />\frac{R}{r} = \frac{R'}{r'},<br />\]<br />donde, como es habitual, $R$ y $r$ denotan los radios de las circunferencias circunscrita e inscrita del $\triangle ABC$ (an\'alogo para $R', r'$). Demostrar que entonces los tri\'angulos son semejantes: $\triangle ABC \sim \triangle A'B'C'$.<br />](./tex/134676.gif)
|
|
|
|
 Oct 23 2006, 11:01 AM Oct 23 2006, 11:01 AM
Publicado:
#74
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
CITA(Cesarator @ Oct 23 2006, 09:45 AM)   screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img253.imageshack.us/img253/9519/soluxxxpm8.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img253.imageshack.us/img253/9519/soluxxxpm8.png');}" />(disculpas... en la biblioteca no tenia programa para geometria) Mensaje modificado por Pasten el Oct 23 2006, 11:42 AM -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
| Cesarator |
 Oct 23 2006, 11:26 AM Oct 23 2006, 11:26 AM
Publicado:
#75
|
|
Invitado |
|
|
|
|
 Oct 23 2006, 02:29 PM Oct 23 2006, 02:29 PM
Publicado:
#76
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Situemos
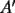 en en 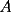 , luego hay 2 casos: , luego hay 2 casos: screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img275.imageshack.us/img275/1550/mmmmav2.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img275.imageshack.us/img275/1550/mmmmav2.png');}" />Ahora notese las siguientes relaciones: 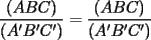 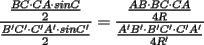 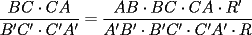 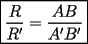 Otra relación útil: 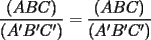 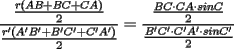 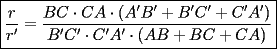 Por lo tanto: 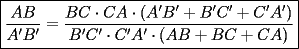 Luego, sea 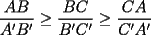 Entonces: 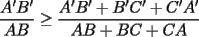 Luego: 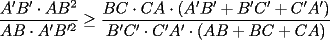 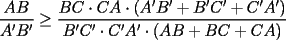 Con la igualdad para 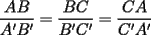 , osea, para , osea, para 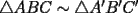 Pero, si sea 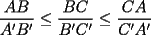 Entonces: 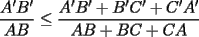 Luego: 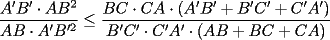 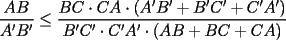 Con la igualdad para 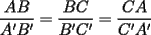 , osea, para , osea, para 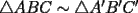
Mensaje modificado por Luffy el Oct 23 2006, 04:31 PM |
|
|
|
 Oct 23 2006, 04:26 PM Oct 23 2006, 04:26 PM
Publicado:
#77
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
CITA(Cesarator @ Oct 22 2006, 04:58 PM)  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img335.imageshack.us/img335/4662/kcuadrilatrovc5.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img335.imageshack.us/img335/4662/kcuadrilatrovc5.png');}" />![TEX: \noindent<br />Demostraresmos previamente la seiguiente desigualdad;\\<br />$x^2+y^2\ge 2xy\sqrt{(1-x^2)(1-y^2)}+2x^2y^2 : x,y\in [0,1]$ (1)\\<br />Primero, tenemos que\\<br />$2xy\sqrt{(1-x^2)(1-y^2)}=2\sqrt{x^2(1-x^2)y^2(1-y^2)}\le x^2(1-x^2)+y^2(1-y^2)=x^2+y^2-(x^4+y^4)$ (2)\\<br />por otra parte, se tiene\\<br />$x^4+y^4\ge 2x^2y^2$ (3)\\<br />De (2) y (3) se desprende que\\<br />$2xy\sqrt{(1-x^2)(1-y^2)}+2x^2y^2\le x^2+y^2-(x^4+y^4)+x^4+y^4=x^2+y^2$\\<br />Como se queria probar. La condicion de igualdad es la misma que la de $A\ge G$, es decir, igualdad si y solo si $x=y$.\\<br />\\<br />Usaremos la notacion del dibujo. Llamemos $p,q$ a las diagonales y $a,b,c,d$ a los lados segun se ve. Sean $u=\angle ACB,v=\angle ACD$. El cuadrilatero rojo es un cuadrado y sus vertices son las intersecciones y centros de los dos arcos grises que se ven. Estos arcos corresponden a los lugares geometricos de $B,D$ cuando varian $u,v$. Digamos que el radio de los arcos es $\frac{1}{2}$, entonces tendremos\\<br />$a=\sin u\\<br />b=\sin v\\<br />c=\sin (45-v)=\frac{1}{\sqrt{2}}(\cos v -b)\\<br />d=\sin (45-u)=\frac{1}{\sqrt{2}}(\cos u -a)\\<br />p^2=a^2+b^2-2ab \cos (45-u-v)=a^2+b^2-2ab(a \cos v+b \cos u)\\<br />q^2=\frac{1}{2}$\\<br />Ahora, por hipotesis sabemos que\\<br />$p^2q^2=2abcd$ (4)\\<br />Sustituyendo y amplificando por $2$ obtenemos\\<br />$a^2+b^2-2ab(a\cos v+b\cos u)=2ab(\cos u -a)(\cos v -b)$\\<br />desarrollando y simplificando obtenemos\\<br />$a^2+b^2=2ab\cos u \cos v + 2a^2b^2$\\<br />ahora recordando que $\sin^2 r + \cos^2 r =1, \forall r\in\mathbb{R}$ obtenemos\\<br />$a^2+b^2=2ab\sqrt{(1-a^2)(1-b^2)} + 2a^2b^2$\\<br />Que es el caso particular de igualdad de (1), luego, la condicion dada (4) implica que $a=b\Rightarrow \sin u=\sin v \Rightarrow u=v$, de donde se concluye que necesariamente $p$ es perpendicular a $q$, como se pedia.\\<br />Respuesta: Las diagonales necesariamente son perpendiculares.<br />](./tex/134903.gif)
Mensaje modificado por Pasten el Oct 23 2006, 05:35 PM -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Oct 23 2006, 06:25 PM Oct 23 2006, 06:25 PM
Publicado:
#78
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 293 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 3 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
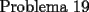  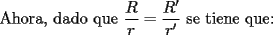 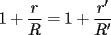 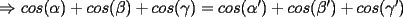 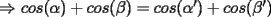 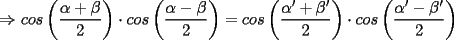 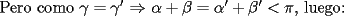 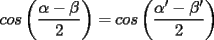 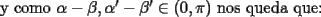 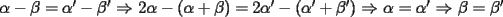 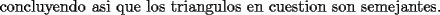
--------------------  |
|
|
|
| Cesarator |
 Oct 23 2006, 06:28 PM Oct 23 2006, 06:28 PM
Publicado:
#79
|
|
Invitado |
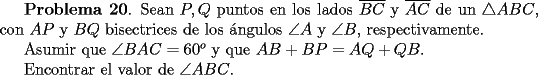
Mensaje modificado por Cesarator el Oct 23 2006, 06:45 PM |
|
|
|
 Oct 23 2006, 06:38 PM Oct 23 2006, 06:38 PM
Publicado:
#80
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 293 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 3 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Pero la medida del
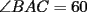 por enunciado por enunciado Mensaje modificado por Caetano el Oct 23 2006, 06:39 PM --------------------  |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 26th April 2025 - 05:56 AM |










![TEX: <br />{\bf Problema 18}. Sea $ABCD$ un cuadril\'atero convexo con $\angle B = \angle D =135^o$. Asumir que<br />\[<br />AC^2\cdot BD^2 = 2 AB\cdot BC\cdot CD\cdot DA.<br />\]<br />Determinar si las diagonales del cuadril\'atero son necesariamente perpendiculares.<br />](./tex/134483.gif)