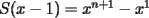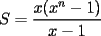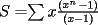|
|
|
|
|
|
|
  |
| Cesarator |
 Aug 19 2006, 10:51 PM Aug 19 2006, 10:51 PM
Publicado:
#11
|
|
Invitado |
nop, a veces el apuro nos hace equivocarnos en cosas elementales...
|
|
|
|
 Aug 19 2006, 11:21 PM Aug 19 2006, 11:21 PM
Publicado:
#12
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Creo que me precipité demasiado....
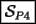 Pintemos el tablero como sigue, de tal forma que los cuadrados rojos de la figura son sólo cuadrados negros del tablero de ajedrez, por lo tanto, al sacar casillas blancas, las negras quedarán intactas, y las rojas también.  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img201.imageshack.us/img201/3188/tableritoci1.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img201.imageshack.us/img201/3188/tableritoci1.png');}" />Vemos que una figura de la forma del problema, sólo cubre una casilla roja , porque es imposible que cubra dos, por lo tanto, en caso de cubrir el casillero, debemos cubrir todas las piezas rojas. Como son 25 casillas rojas, se necesitarán 25 figuras para cubrir todas las casillas rojas. Como el problema nos dice que son 24, entonces nos quedará una casilla roja sin cubrir, luego no es posible cubrir el casillero. Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Aug 20 2006, 03:22 AM Aug 20 2006, 03:22 AM
Publicado:
#13
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
CITA(Cesarator @ Aug 12 2006, 10:47 PM) ![TEX: <br />{\bf Problema 1}. Sean $x,y,z>0$ tales que $\displaystyle \frac{1}{x^2} + \frac{1}{y^2}+ \frac{1}{z^2} =1$. Demostrar la desigualdad<br />\[<br />\frac{xy}{xy-1} + \frac{yz}{yz-1} + \frac{zx}{zx-1} \le \frac{9}{2}.<br />\]<br />](./tex/108382.gif)  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img209.imageshack.us/img209/845/problema1kn9.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img209.imageshack.us/img209/845/problema1kn9.png');}" />Como la sorpresa de la mañana fue que ya se habia resuelto por Schur, me vi obligado a ver por otro lado...  ![TEX: \noindent<br />Ahora la demostracion;<br />Por todo lo anterior\\<br />$b=|v|=A\cos(45+t)\\<br />c=|w|=A\cos(45-t)$\\<br />donde $A=sen\alpha$\\<br />Ahora tenemos\\<br />$\displaystyle <br />\sum_{cic}\frac{1}{1-ab}=\\<br />\frac{1}{1-A^2cos(45+t)}+\frac{1}{1-A^2cos(45-t)}+<br />\frac{1}{1-A^2cos(45-t)cos(45-t)}$\\<br />Por las formulas trigonometricas de suma y diferencia de angulos tenemos que\\<br />$\displaystyle<br />\sqrt{2}cos(45-t)=cos(t)+sen(t)\\<br />\sqrt{2}cos(45+t)=cos(t)-sen(t)\\<br />2cos(45-t)cos(45+t)=cos(2t)$\\<br />Fijando ahora $k: kA^2=\sqrt{2}$ y usando lo anterior\\<br />$\displaystyle <br />\frac{1}{k}\sum_{cic}\frac{1}{1-ab}=\\<br />\frac{1}{k-[cos(t)-sen(t)]}+\frac{1}{k-[cos(t)+sen(t)]}+<br />\frac{\sqrt{2}}{\sqrt{2}k-cos(2t)}$\\<br />Sabemos por hipotesis que $0\le t\le 45$ asi que podemos considerar los senos y cosenos positivos. Es mas, si definimos $p=sen (t)$ tendremos que $0\le p\le \frac{1}{\sqrt{2}}$ y si recordamos que $cos(2t)=1-2sen^2(t)$ obtendremos al sustituir\\<br />$\displaystyle <br />\frac{1}{k}\sum_{cic}\frac{1}{1-ab}=\\<br />\frac{1}{k+p-\sqrt{1-p^2}}+\frac{1}{k-p-\sqrt{1-p^2}}+<br />\frac{\sqrt{2}}{\sqrt{2}k-1+2p^2}$\\<br />Llamemos $f(p)$ a la expresion anterior (no olvidemos que $k$ esta fijo, para el caso es una constante).](./tex/111207.gif) ![TEX: \noindent<br />$f(p)$ es una funcion racional sin singularidades para $p\in[0,\frac{1}{\sqrt{2}}]$ porque\\<br />$kA^2=\sqrt{2}\Rightarrow k=\frac{\sqrt{2}}{sen^2\alpha}>\sqrt{2}$\\<br />$k>\sqrt{2}\ge sen(t)+cos(t)=p+\sqrt{1-p^2}\ge -p+\sqrt{1-p^2}$<br />por test de la primera derivada para hayar el maximo. De aqui se deduce la no-singularidad de la primera y segunda fraccion en $f(p)$. El denominador de la tercera fraccion es claro que no se anula porque $\sqrt{2}k>2$.\\<br />Asi que $f(p)$ es continua para $p\in[0,\frac{1}{\sqrt{2}}]$.\\<br />Se tiene\\<br />$\displaystyle <br />f'(p)=\\<br />-\frac{\sqrt{1-p^2}+p}{\sqrt{1-p^2}(\sqrt{1-p^2}-p-k)^2}+<br />\frac{\sqrt{1-p^2}-p}{\sqrt{1-p^2}(\sqrt{1-p^2}+p-k)^2}-<br />\frac{4\sqrt{2}p}{(\sqrt{2}k-1+2p^2)^2}$\\<br />que es continua porque los factores problematicos de los denominadores son los mismos que mas arriba se probo que no se anulaban.\\<br />Busquemos los $p$ de nuestro dominio para los cuales $f'(p)=0$](./tex/111208.gif) ![TEX: \noindent<br />Se debe resolver la ecuacion\\<br />$\displaystyle<br />\frac{\sqrt{1-p^2}+p}{\sqrt{1-p^2}(\sqrt{1-p^2}-p-k)^2}+<br />\frac{4\sqrt{2}p}{(\sqrt{2}k-1+2p^2)^2}=<br />\frac{\sqrt{1-p^2}-p}{\sqrt{1-p^2}(\sqrt{1-p^2}+p-k)^2}$\\<br />Esto parece una abominacion, pero observemos que el segundo termino es no negativo, mas aun, como $0\le p\le \frac{1}{\sqrt{2}}$ se tiene\\<br />$\displaystyle<br />\frac{[\sqrt{1-p^2}]+[p]}{\sqrt{1-p^2}([\sqrt{1-p^2}-k]-[p])^2}\ge<br />\frac{[\sqrt{1-p^2}]-[p]}{\sqrt{1-p^2}([\sqrt{1-p^2}-k]+[p])^2}$\\<br />porque\\<br />$[\sqrt{1-p^2}]+[p]\ge [\sqrt{1-p^2}]-[p]$\\<br />$[\sqrt{1-p^2}-k]-[p]\le [\sqrt{1-p^2}-k]+[p]$\\<br />con igualdad (dentro del dominio) solo cuando $p=0$. Afortunadamente es facil comprobar que $p=0$ es una solucion de la ecuacion, y por las desigualdades anteriores es la unica en el dominio.](./tex/111209.gif)  ----------- Editado: algunas mayusculas por ahi... el post fue hecho como a las 4 de la mañana asi que habia algunos errores de tipeo. Mensaje modificado por Pasten el Aug 20 2006, 11:48 AM -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Aug 20 2006, 11:29 AM Aug 20 2006, 11:29 AM
Publicado:
#14
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
-------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Aug 20 2006, 12:20 PM Aug 20 2006, 12:20 PM
Publicado:
#15
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 519 Registrado: 22-April 06 Desde: Concepción Miembro Nº: 925 Nacionalidad:  Sexo:  |
CITA(Cesarator @ Aug 19 2006, 10:51 PM) Se me adelantaron... Bueno, por lo menos puedo usar una figura "parecida"  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img411.imageshack.us/img411/5541/km4oc4.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img411.imageshack.us/img411/5541/km4oc4.png');}" />Vemos que, del las 81 casillas del tablero (41 negras y 40 blancas) quedan 72 (41 negras y 31 blancas), como deben ser cubiertas con 24 fichas de 3 casillas cada una, que son: n piezas de la forma N, esto es, formadas por 2 casillas negras con la casilla del vértice blanca; b piezas de la forma B, esto es, formadas por 2 casillas blancas con la casilla del vértice negra. Igualando las cantidades de casillas de cada color 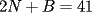 (casillas negras) (casillas negras)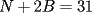 (casillas blancas) (casillas blancas)llegamos a que se necesitan 17 piezas de la forma N. Miramos ahora mi "original" diagrama, y vemos que tanto las casillas negras como las rojas simbolizan casilleros negros del tablero, que no han sido removidos; y que cada pieza de la forma N debe cubrir exactamente uno de los casilleros rojos y uno de los negros. Pero hay sólo 16 casilleros con puntos negros, luego no se pueden cubrir con las 17 piezas N. En conclusión, es imposible cubrir el tablero de la forma planteada. P.D.: este es el post número 20000!!! -------------------- There is a theory which states that if ever anyone discovers exactly what the Universe is for and why is it here, it will instantly disappear and be replaced by something even more bizarre and inexplicable.
There is another theory which states that this has already happened. - Adams, The Restaurant at the End of the Universe ----------------------------------- Existe una teoría que postula que si alguien alguna vez llega a descubrir exactamente para qué es el Universo y por qué está aquí, éste desaparecerá instantáneamente y será reemplazado por algo aún más extraño e inexplicable. Existe otra teoría que dice que esto ya ha ocurrido. - Adams, el Restorán al Final del Universo |
|
|
|
| Cesarator |
 Aug 20 2006, 01:33 PM Aug 20 2006, 01:33 PM
Publicado:
#16
|
|
Invitado |
wow! excelente! no tienen piedad con este pobre anciano y me dan muuucho trabajo.
En todo caso, contento de este tipo de trabajo! Ya avanzaremos en la correccion detallada de todas vuestras soluciones, lo que corresponde ahora es el siguiente problema, que sera un "clasico": ![TEX: <br />{\bf Problema 5}. Sea $C_n$ el n\'umero de d\'{\i}gitos cero que contiene la escritura decimal del n\'umero $n$ (Por ejemplo, $C_{10}=1$). Calcular el valor de la suma<br />\[<br />2^{C_1} + 2^{C_2} +...+ 2^{C_{9999999999}}.<br />\]<br />](./tex/111246.gif) Error de tipeo corregido Mensaje modificado por Cesarator el Aug 20 2006, 01:43 PM |
|
|
|
 Aug 20 2006, 02:47 PM Aug 20 2006, 02:47 PM
Publicado:
#17
|
|
 Máquina que convierte café en teoremas Grupo: Colaborador Silver Mensajes: 1.665 Registrado: 18-August 05 Desde: Concepción Miembro Nº: 247 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Si
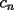 contiene n ceros en su escritura decimal, entonces. contiene n ceros en su escritura decimal, entonces.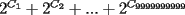 se puede escribir como 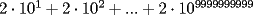 Factorizando: 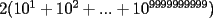 Vemos que claramente se ha formado una sumatoria de igual base y exponetentes enteros sucesivos. Esta sumatoria (su formula es) 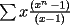 Reemplazando los datos tenemos. 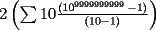 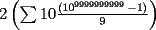 --------------------  Manual para subir imágenes y archivos a fmat (con servidor propio) Manual de latex Estilo Propio Lista de libros en fmat    "Un Matemático es una máquina que trasforma café en teoremas"(Erdös) --- Consultas, sugerencias, reclamos via mp o a los correos mencionados. |
|
|
|
 Aug 20 2006, 02:59 PM Aug 20 2006, 02:59 PM
Publicado:
#18
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
CITA 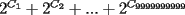 se puede escribir como 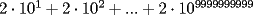 Porque afirmas esto? Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Aug 20 2006, 03:01 PM Aug 20 2006, 03:01 PM
Publicado:
#19
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 519 Registrado: 22-April 06 Desde: Concepción Miembro Nº: 925 Nacionalidad:  Sexo:  |
Primero fijemos trabajaremos sólo con los números de una cantidad
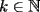 fija de dígitos. fija de dígitos.Nunca el primer dígito es un cero, luego, para todos los números 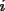 de de 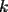 dígitos, dígitos,  Para 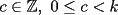 , la cantidad de números de , la cantidad de números de 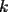 dígitos con dígitos con  ceros es ceros es Luego la suma de todos los 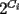 , con , con 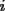 número de número de 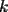 dígitos, es dígitos, es![TEX: \[<br />\sum\limits_{c = 0}^{k - 1} {2^c \left( {\frac{{(k - 1)!}}<br />{{c!(k - 1 - c)!}}9^{k - c} } \right) = 9\sum\limits_{c = 0}^{k - 1} {\frac{{(k - 1)!}}<br />{{c!(k - 1 - c)!}}9^{k - 1 - c} } 2^c = 9\left( {9 + 2} \right)^{k - 1} } <br />\]<br />](./tex/111468.gif) Y la suma buscada, correspondiente a la de todos los números de 1 hasta 10 dígitos, es ![TEX: \[<br />\sum\limits_{k = 1}^{10} {9\left( {9 + 2} \right)^{k - 1} = 9 \cdot \frac{{11^{10} - 1}}<br />{{10}}} <br />\]](./tex/111469.gif)
-------------------- There is a theory which states that if ever anyone discovers exactly what the Universe is for and why is it here, it will instantly disappear and be replaced by something even more bizarre and inexplicable.
There is another theory which states that this has already happened. - Adams, The Restaurant at the End of the Universe ----------------------------------- Existe una teoría que postula que si alguien alguna vez llega a descubrir exactamente para qué es el Universo y por qué está aquí, éste desaparecerá instantáneamente y será reemplazado por algo aún más extraño e inexplicable. Existe otra teoría que dice que esto ya ha ocurrido. - Adams, el Restorán al Final del Universo |
|
|
|
| Cesarator |
 Aug 20 2006, 04:12 PM Aug 20 2006, 04:12 PM
Publicado:
#20
|
|
Invitado |
Bien! el p4 es de una olimpiada internacional que precisare mas adelante, y el P5 es un problema ya clasico de la olimpiada de Hungria, año 1981.
Ya se actualizaran los puntajes. Vamos al ![TEX: <br />{\bf Problema 6}. Dos jugadores, \'Alvaro (A) y Benito (B) insertan por turnos uno de los s\'{\i}mbolos $+$, $-$ o $\times$ en cualquiera de los espacios dejados entre los n\'umeros del 1 al 100:<br />\[<br />1 \ \ 2 \ \ 3 \ \ 4 \ \ ... \ \ 99 \ \ 100.<br />\]<br />Al terminar y realizar las operaciones, el resultado es un n\'umero $S$. Demostrar que el primer jugador (A) puede hacer que el resultado sea par o impar, seg\'un lo desee (Recordar que las multiplicaciones se realizan antes que las sustracciones y adiciones).<br />](./tex/111492.gif)
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 11th July 2025 - 02:40 AM |













 [attachment=1017:attachment]
[attachment=1017:attachment]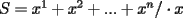
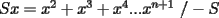
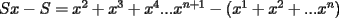 por suma telescopica.
por suma telescopica.