|
|
|
|
|
|
|
  |
 Aug 5 2006, 07:57 PM Aug 5 2006, 07:57 PM
Publicado:
#1
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 90 Registrado: 14-May 05 Desde: 33º30'S 70º40'O Miembro Nº: 18 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Dado un número positivo n, definimos el conjunto asociado a n (que llamaremos A(n)), como el conjunto de todos los números obtenidos al permutar los dígitos de n. Si n tuviese dígitos repetidos, entonces algunas permutaciones coincidirían, en este caso no debemos repetir estas permutaciones. Además, si n tuviese dígitos 0, algunas de estas permutaciones coincidirán, en este casose obtienen números con menos dígitos, que sí deben ser considerados en el conjunto asociado.
Por ejemplo el conjunto asociado a 2006 es: A(2006)={26,62,206,260,2006,2060,2600,6002,6020,6200} En este ejemplo, los dígitos de 2006 pueden desordenarse para obtener 0602, esto explica que el número 602 esté en el conjunto A(2006). El mismo tipo de argumentos explica la presencia de todos los elementos de A(206) que son menores de mil. Una vez conocidos los elementos de A(n), podemos definir las siguientes cantidades: · La suma asociada a n (que llamaremos s(n)) es la suma de todos los elementos de A(n). · El promedio asociado a n (que llamaremos x(n)) es el promedio de todos los elementos de A(n). · El menor asociado a n (que llamaremos m(n)) es el menor elemento de A(n). · El mayor asociado a n (que llamaremos M(n)) es el mayor elemento asociado a A(n). Por otra parte diremos que un número es k-especial si tiene k dígitos (el primero de ellos debe ser distinto de cero) y todos son distintos. Diremos que un número es especial si es k-especial para algún valor de k. Diremos que un número es curioso si x(n) = n. Problema 1. (a) Explique por qué razón los números 10-especiales son múltiplos de 9. Encuentre también dos números 10-especiales cuya diferencia sea 9. De todo lo anterior, el máximo común divisor de todos los números 10-especiales será igual a 9. (b) Para cada 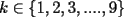 encuentre un número k-especial que no sea múltiplo de 9, y encuentre también dos números k-especiales conscutivos. encuentre un número k-especial que no sea múltiplo de 9, y encuentre también dos números k-especiales conscutivos.De este modo, para cada 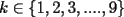 , el máximo común divisor de todos los números k-especiales será igual a 1. , el máximo común divisor de todos los números k-especiales será igual a 1.Problema 2. (a) Encuentre un número curioso con 5 cifras. (b) Encuentre un número curioso con 2006 cifras. Problema 3. Encuentre todos los números curiosos menores que cien. Problema 4. (a) Considere los números: n = 1234567891011121314151617....19992000200120022003200420052006 ñ = 20062005200420032002200120001999.....17161514131210987654321 ¿Qué puede decirse de los conjuntos A(n) y A(ñ)? (b) Inicialmente tenemos un número n, y al desordenar sus dígitos obtenemos un número ñ. Supongamos que n y ñ tienen la misma cantidad de dígitos. Compare los conjuntos A(n) y A(ñ). Problema 5. Sea n un número con la siguiente propiedad: existen dos dígitos de n, que llamaremos a y b, tales que a<b y a está a la izquierda de b(en la representación decimal de n). Encuentre un número ñ>n tal que s(n)=s(ñ). Problema 6. (a) Si un número 4-especial n tiene dígitos a,b,c,d leídos de izquierda a derecha, encuentre una fórmula para x(n). (b)Un mago propone realizar el siguiente truco: una persona del público, designada al azar, elige un número 4-especial n (el mago sabe que este número debe ser 4-especial, aunque no conoce su valor preciso). La persona calcula x(n) e informa de este valor al mago. Con esta nueva información, el mago determina si el número es divisible por 9 ¿Por qué razon este truco siempre funciona? Mensaje modificado por felipe_contreras(IN) el May 3 2007, 07:52 PM -------------------- "El único primo congruente a uno en módulo cuatro es cinco" A. Gajardo
""I'm going to try to see if I can remember as much to make it sound like I'm smart on the subject."—G. W. Bush, answering a question concerning a possible flu pandemic, Cleveland, July 10, 2007 "I aim to be a competitive nation."—G. W. Bush, San Jose, Calif., April 21, 2006 "Those who enter the country illegally violate the law."— G. W. Bush, Tucson, Ariz., Nov. 28, 2005 "Our enemies are innovative and resourceful, and so are we. They never stop thinking about new ways to harm our country and our people, and neither do we." — G. W. BushWashington, D.C., Aug. 5, 2004 |
|
|
|
 Aug 5 2006, 08:05 PM Aug 5 2006, 08:05 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.605 Registrado: 25-June 05 Miembro Nº: 123 Colegio/Liceo:  Universidad:  Sexo:  |
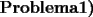   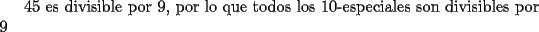 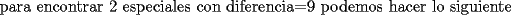 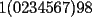 [1] [1]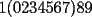 [2] [2]![TEX: [1]-[2]=9](./tex/105679.gif) 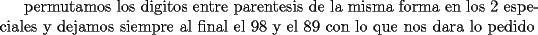
-------------------- |
|
|
|
 Aug 7 2006, 06:09 PM Aug 7 2006, 06:09 PM
Publicado:
#3
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 16 Registrado: 21-April 06 Miembro Nº: 897 |
Problema 4:
para a) y b) es: se pueden obtener iguales permutaciones s(n)=s(ñ) x(n)=x(ñ) m(n)=m(ñ) M(n)=M(n) esto segun yo... si alguien quiere agregar otra cosa por favor hagalo... o correcciones y mas... --------------------  |
|
|
|
 Aug 7 2006, 06:13 PM Aug 7 2006, 06:13 PM
Publicado:
#4
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 16 Registrado: 21-April 06 Miembro Nº: 897 |
Problema 2:
a) podia ser un numero de 5 cifras y todas iguales 55555 b)lo mismo que antes pero 2006 cifras... 5555555......55555/ 2006 veces denuevo necesito correcciones y opiniones y mas... --------------------  |
|
|
|
 Aug 7 2006, 06:14 PM Aug 7 2006, 06:14 PM
Publicado:
#5
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 16 Registrado: 21-April 06 Miembro Nº: 897 |
Problema 3:
los numero curiosos menores de 100 son (o eran): 1 2 3 4 5 6 7 8 9 11 22 33 44 55 66 77 88 99 --------------------  |
|
|
|
 Aug 7 2006, 06:38 PM Aug 7 2006, 06:38 PM
Publicado:
#6
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 129 Registrado: 20-June 05 Desde: Santiago ^^ Miembro Nº: 115 Nacionalidad:  Sexo:  |
El problema 5 con mi grupo lo imaginamos de la siguiente forma:
Si hay un número n con la condición de que 2 de sus dígitos sean "a" y "b" y que se cumpla que : 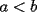 y con "a" a la izquierda de "b". y con "a" a la izquierda de "b".Entonces llamamos a: 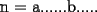 y que: y que: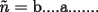 Considerando que n y ñ tienen el mismo número de cifras y la misma cantidad de digitos iguales, sólo que permutadas. Entonces ahí se cumpliría que: 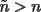 y que y que 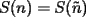 Salu2 |
|
|
|
 Aug 7 2006, 10:31 PM Aug 7 2006, 10:31 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Los problemas 1 y 2 están bien respondidos... nada que objetar
El problema 4 se puede responder en pocas palabras, pero aquí no está hecho de esa manera. Lo único que veo es un listado de afirmaciones sin mucha explicación. La solución al problema 3, dada aquí, tiene exactamente todos los números curiosos menores que 100, pero no ha explicado por qué descartar los otros números. Sobre el problema 5: en primer lugar, el símbolo ñ se puede hacer en modo matemático (LaTeX) como $\tilde{n}$. Luego de eso, la solución es correcta, e incluso el mismo argumento sirve para el problema 4. En resumen, falta que se respondan los ejercicios 3, 4 y 6 -------------------- |
|
|
|
 Aug 7 2006, 10:42 PM Aug 7 2006, 10:42 PM
Publicado:
#8
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
A mi me tocó intervenir en el problema 4, así que procedo a exponer mi solución
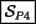 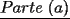    Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Aug 7 2006, 10:56 PM Aug 7 2006, 10:56 PM
Publicado:
#9
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Esta también me tocó a mi
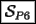 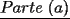  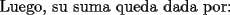 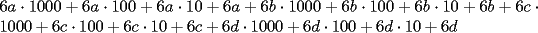 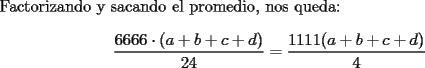    Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Aug 8 2006, 05:45 PM Aug 8 2006, 05:45 PM
Publicado:
#10
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 129 Registrado: 20-June 05 Desde: Santiago ^^ Miembro Nº: 115 Nacionalidad:  Sexo:  |
 Para: 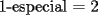 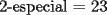 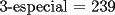 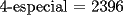 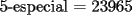 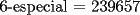 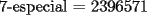 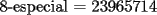 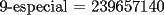 Y con los consecutivos: 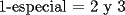 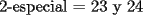 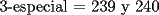 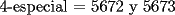 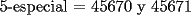 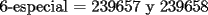 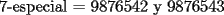  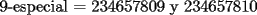 Y ahí estaría la parte "b" de la pregunta uno... |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 02:54 PM |










