Tercer Nivel Individual - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > Campeonato Interescolar > Campeonato Interescolar 2006 > Quinta Fecha(Recuperativa)

2 Páginas:

1 2 >

Reply to this topic

Start new topic

Tercer Nivel Individual, Octava Region

GlagosSA Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 5 2006, 04:32 PM Publicado: #1
Dios Matemático Grupo: Usuario FMAT Mensajes: 380 Registrado: 22-April 06 Desde: Chillan, chile, sudamerica, el mundo Miembro Nº: 912 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \noindent La ultima fecha del campeonato 2006, muy entretenida$ $TEX: \noindent Posteen sus solutions, jejejeje$ pd: kenshin, ahora la imagen no deforma el foro toy cumpliendo las reglas Archivo(s) Adjunto(s) hola2.JPG ( 31.38k ) Número de descargas: 3 -------------------- Un dia aciago del año 212 a.C., durante la segunda querra punica, Arquimedes se encontraba contemplando algunos circulos que tenia dibujados sobre la arena. Un soldado romano trató de interrumpirlo. La reaccion del genio frente a la presencia del enemigo invasor, el lugar de ser miedo, fue indignacion por verse interrumpido en su trabajo intelectual.-"¡deje en paz a mis circulos!"- Unos minutos mas tarde, el maestro matematico de 75 años, muere atravesado por una espada romana. La altura de tu Vuelo dependera del tamaño de los Ideales que lleves por Alas.. El beso es la distancia mas corta entre Tú y Yo..

GlagosSA Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 5 2006, 04:59 PM Publicado: #2
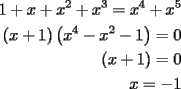Dios Matemático Grupo: Usuario FMAT Mensajes: 380 Registrado: 22-April 06 Desde: Chillan, chile, sudamerica, el mundo Miembro Nº: 912 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	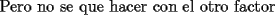$TEX: \noindent Aca mi solucion a la primera$ $TEX: <br />\begin{equation}<br />\begin{aligned}<br /> 1 + x + x^2 + x^3 = x^4 + x^5 \\ <br /> \left( {x + 1} \right)\left( {x^4 - x^2 - 1} \right) = 0 \\ <br /> (x + 1) = 0 \\ <br /> x = - 1 \\ <br />\end{aligned}<br />\end{equation}<br />$ $TEX: \noindent Pero no se que hacer con el otro factor$ -------------------- Un dia aciago del año 212 a.C., durante la segunda querra punica, Arquimedes se encontraba contemplando algunos circulos que tenia dibujados sobre la arena. Un soldado romano trató de interrumpirlo. La reaccion del genio frente a la presencia del enemigo invasor, el lugar de ser miedo, fue indignacion por verse interrumpido en su trabajo intelectual.-"¡deje en paz a mis circulos!"- Unos minutos mas tarde, el maestro matematico de 75 años, muere atravesado por una espada romana. La altura de tu Vuelo dependera del tamaño de los Ideales que lleves por Alas.. El beso es la distancia mas corta entre Tú y Yo..

Gazoo Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 5 2006, 05:09 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.112 Registrado: 21-December 05 Desde: El Bosque - Stgo Miembro Nº: 473 Colegio/Liceo: Universidad: Sexo:	Tal vez sea útil hacer un cambio de variable en el segundo factor para resolverlo como ecuación Bicuadrática. -------------------- "El sentido común es el conjunto de todos los prejuicios adquiridos antes de los 18 años" A. Einstein. Estudiante Ingeniería Civil Eléctrica - DIE USACH

「Krizalid」 Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 5 2006, 05:11 PM Publicado: #4
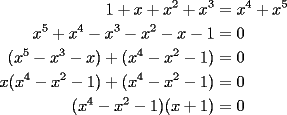Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad: Sexo:	$TEX: \begin{equation}<br />\begin{aligned}<br /> 1 + x + x^2 + x^3 &= x^4 + x^5 \\ <br /> x^5 + x^4 - x^3 - x^2 - x - 1 &= 0 \\ <br /> (x^5 - x^3 - x) + (x^4 - x^2 - 1) &= 0 \\ <br /> x(x^4 - x^2 - 1) + (x^4 - x^2 - 1) &= 0 \\ <br /> (x^4 - x^2 - 1)(x + 1) &= 0 \\ <br />\end{aligned}<br />\end{equation}<br />$ $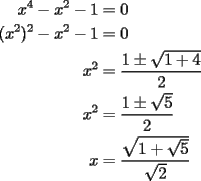TEX: \begin{equation}<br />\begin{aligned}<br /> x^4 - x^2 - 1 &= 0 \\ <br /> (x^2 )^2 - x^2 - 1 &= 0 \\ <br /> x^2 &= \frac{{1 \pm \sqrt {1 + 4} }}<br />{2} \\ <br /> x^2 &= \frac{{1 \pm \sqrt 5 }}<br />{2} \\ <br /> x &= \frac{{\sqrt {1 + \sqrt 5 } }}<br />{{\sqrt 2 }} \\ <br />\end{aligned}<br />\end{equation}<br />$

.r0 Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 5 2006, 05:30 PM Publicado: #5
Dios Matemático Grupo: Usuario FMAT Mensajes: 452 Registrado: 28-January 06 Desde: Quirihue, VIII Region Miembro Nº: 519 Nacionalidad: Universidad: Sexo:	krizalid: esta bien tu desarrollo, pero que paso con el "mas o menos"? estas perdiendo soluciones, ese polinomio de grado 5, tiene 5 soluciones, una la expuso GlagosSA, y las otras 4 se extraen de tu desarrollo... Retomando lo que tu dijiste: $TEX: \[<br />\begin{array}{l}<br /> x^2 = \dfrac{{1 \pm \sqrt 5 }}{2} \\ <br /> \\ <br /> x = \pm \sqrt {\dfrac{{1 \pm \sqrt 5 }}{2}} \\ <br /> \end{array}<br />\]$ lo cual, racionalizado (para que se vea mas lindo ) $TEX: \[<br />x = \pm \dfrac{{\sqrt {1 \pm \sqrt 5 } }}{{\sqrt 2 }} = \pm \dfrac{{\sqrt {1 \pm \sqrt 5 } }}{{\sqrt 2 }} \cdot \dfrac{{\sqrt 2 }}{{\sqrt 2 }} = \pm \dfrac{{\sqrt 2 \cdot \sqrt {1 \pm \sqrt 5 } }}{{\left( {\sqrt 2 } \right)^2 }} = \pm \dfrac{{\sqrt {2 \cdot (1 \pm \sqrt 5 )} }}{2} = \pm \dfrac{{\sqrt {2 \pm 2\sqrt 5 } }}{2}<br />\]$ Entonces, la respuesta final sería: $TEX: \[<br />x = \left\{ { - 1,\frac{{\sqrt {2 + 2\sqrt 5 } }}{2},\frac{{\sqrt { - 2 + 2\sqrt 5 } }}{2}i, - \frac{{\sqrt {2 + 2\sqrt 5 } }}{2}, - \frac{{\sqrt { - 2 + 2\sqrt 5 } }}{2}i} \right\}<br />\]$ (la raices complejas: factorizen por -1, y extraigan la raiz) PD: alguien sabe si se puede y como "tarjar" en latex? (como para haber tarjado el exponente 2 y la raiz cuadrada...) -------------------- Nicolás Flores Cartes Estudiante de Ingeniería y Ciencias. Plan Común Universidad de Chile

「Krizalid」 Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 5 2006, 05:37 PM Publicado: #6
Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad: Sexo:	Déjame ir a buscar las soluciones

GlagosSA Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 5 2006, 07:33 PM Publicado: #7
Dios Matemático Grupo: Usuario FMAT Mensajes: 380 Registrado: 22-April 06 Desde: Chillan, chile, sudamerica, el mundo Miembro Nº: 912 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \noindent Sabia que habia que hacer eso, de echo lo hice pero no lo quise poner en la solucion, lo escribi, lo borre y encima le puse un tollo heavy. Bueno que me sirva de experiencia$ -------------------- Un dia aciago del año 212 a.C., durante la segunda querra punica, Arquimedes se encontraba contemplando algunos circulos que tenia dibujados sobre la arena. Un soldado romano trató de interrumpirlo. La reaccion del genio frente a la presencia del enemigo invasor, el lugar de ser miedo, fue indignacion por verse interrumpido en su trabajo intelectual.-"¡deje en paz a mis circulos!"- Unos minutos mas tarde, el maestro matematico de 75 años, muere atravesado por una espada romana. La altura de tu Vuelo dependera del tamaño de los Ideales que lleves por Alas.. El beso es la distancia mas corta entre Tú y Yo..

GlagosSA Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 5 2006, 07:37 PM Publicado: #8
Dios Matemático Grupo: Usuario FMAT Mensajes: 380 Registrado: 22-April 06 Desde: Chillan, chile, sudamerica, el mundo Miembro Nº: 912 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(.r0 @ Aug 5 2006, 06:30 PM) $TEX: \[<br />x = \left\{ { - 1,\frac{{\sqrt {2 + 2\sqrt 5 } }}{2},\frac{{\sqrt { - 2 + 2\sqrt 5 } }}{2}i, - \frac{{\sqrt {2 + 2\sqrt 5 } }}{2}, - \frac{{\sqrt { - 2 + 2\sqrt 5 } }}{2}i} \right\}<br />\]$ $TEX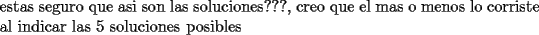: \noindent estas seguro que asi son las soluciones???, creo que el mas o menos lo corriste al indicar las 5 soluciones posibles$ -------------------- Un dia aciago del año 212 a.C., durante la segunda querra punica, Arquimedes se encontraba contemplando algunos circulos que tenia dibujados sobre la arena. Un soldado romano trató de interrumpirlo. La reaccion del genio frente a la presencia del enemigo invasor, el lugar de ser miedo, fue indignacion por verse interrumpido en su trabajo intelectual.-"¡deje en paz a mis circulos!"- Unos minutos mas tarde, el maestro matematico de 75 años, muere atravesado por una espada romana. La altura de tu Vuelo dependera del tamaño de los Ideales que lleves por Alas.. El beso es la distancia mas corta entre Tú y Yo..

Zirou Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 5 2006, 07:41 PM Publicado: #9
Máquina que convierte café en teoremas Grupo: Colaborador Silver Mensajes: 1.665 Registrado: 18-August 05 Desde: Concepción Miembro Nº: 247 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	En el p1 hice un procedimiento muy largo y llegue a cosas engorrosas (al dividir tuve que mencionar que x distinto de 0 y -1) y llegue a 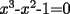$TEX: $x^3$-$x^2$-1=0$ cuide mis pasos y la verdad de ahi en adelante nose como resolver pero claro sabiedno que una solucion es x=-1 -------------------- $TEX: $mathcal{Z}$ $imath$ $Re$ $varnothing$ $mho$$ Manual para subir imágenes y archivos a fmat (con servidor propio) Manual de latex Estilo Propio Lista de libros en fmat "Un Matemático es una máquina que trasforma café en teoremas"(Erdös) --- Consultas, sugerencias, reclamos via mp o a los correos mencionados.

GlagosSA Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 5 2006, 08:31 PM Publicado: #10
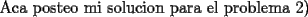Dios Matemático Grupo: Usuario FMAT Mensajes: 380 Registrado: 22-April 06 Desde: Chillan, chile, sudamerica, el mundo Miembro Nº: 912 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	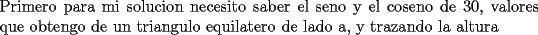$TEX: \noindent Aca posteo mi solucion para el problema 2)$ $TEX: \noindent Primero para mi solucion necesito saber el seno y el coseno de 30, valores que obtengo de un triangulo equilatero de lado a, y trazando la altura$ $TEX: <br />\[<br />\begin{array}{l}<br /> \displaystyle\sin (30) = \frac{{\frac{a}{2}}}{a} = \frac{1}{2} \\ <br /> \displaystyle\cos (30) = \frac{{\frac{{a\sqrt 3 }}{2}}}{a} = \frac{{\sqrt 3 }}{2} \\ <br /> \end{array}<br />\]<br />$ $TEX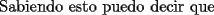: \noindent Sabiendo esto puedo decir que$ $TEX: <br />\[<br />\begin{array}{l}<br /> \overline {AC} = \sin (30)\cdot20 = 10 \\ <br /> \overline {CB} = \cos (30)\cdot20 = 10\sqrt 3 \\ <br /> \end{array}<br />\]<br />$ $TEX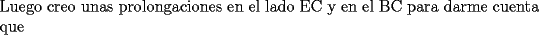: \noindent Luego creo unas prolongaciones en el lado EC y en el BC para darme cuenta que$ $TEX: <br />\[<br />\begin{array}{l}<br /> \angle ABC = \angle BCI = 30 \\ <br /> \angle CAB = \angle ECD = 60 \\ <br /> \angle FEC = \angle ACI = 120 \\ <br /> \end{array}<br />\]<br />$ $TEX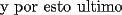: \noindent y por esto ultimo$ $TEX: <br />\[<br />\overline {FE} = \overline {AC} = 10<br />\]<br />$ $TEX: \noindent Asi tengo una buena base para afrontar el problema (aunque ya estamos a la mitad de afrontado), Luego noto que el $\triangle ABC$ es la mitad de un triangulo equilatero, y como D es el pto medio, digo que $\overline{AC}$ es el lado del triangulo. Asi$ $TEX: <br />\[<br />\overline {ED} = \frac{{10\sqrt 3 }}{2} = 5\sqrt 3 <br />\]<br />$ $TEX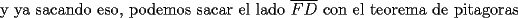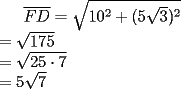: \noindent y ya sacando eso, podemos sacar el lado $\overline{FD}$ con el teorema de pitagoras$ $TEX: $<br /> \overline {FD} = \sqrt {10^2 + (5\sqrt 3 )^2 } \\ <br /> = \sqrt {175} \\ <br /> = \sqrt {25\cdot 7} \\ <br /> = 5\sqrt {7} \\ <br />$<br />$ -------------------- Un dia aciago del año 212 a.C., durante la segunda querra punica, Arquimedes se encontraba contemplando algunos circulos que tenia dibujados sobre la arena. Un soldado romano trató de interrumpirlo. La reaccion del genio frente a la presencia del enemigo invasor, el lugar de ser miedo, fue indignacion por verse interrumpido en su trabajo intelectual.-"¡deje en paz a mis circulos!"- Unos minutos mas tarde, el maestro matematico de 75 años, muere atravesado por una espada romana. La altura de tu Vuelo dependera del tamaño de los Ideales que lleves por Alas.. El beso es la distancia mas corta entre Tú y Yo..

« Posterior · Quinta Fecha(Recuperativa) · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 08:44 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.