Controles 11, 12, 13 y 14, bachi mate II - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad de Chile > Matemáticas 2

3 Páginas:

1 2 3 >

Reply to this topic

Start new topic

Controles 11, 12, 13 y 14, bachi mate II, megamix matematico

Naxoo Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 21 2008, 08:39 PM Publicado: #1
Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \[<br />\begin{gathered}<br /> \boxed{{\text{Control 11}}} \hfill \\<br /> \hfill \\<br /> 1.{\text{ Encuentre un intervalo I y una serie de potencias de la forma }}\sum\limits_{n = 0}^\infty {a_n x^n } {\text{ tal que}} \hfill \\<br /> {\text{sea igual a la funcion }}f:I \to \mathbb{R};f(x) = \frac{1}<br />{{3 + x}} \hfill \\<br /> \hfill \\<br /> 2.{\text{ Determine el radio de convergencia de la serie }}\sum\limits_{n = 0}^\infty {\frac{{n!x^n }}<br />{{n^n }}} \hfill \\<br /> \hfill \\<br /> \boxed{{\text{Control 12}}} \hfill \\<br /> \hfill \\<br /> 1.{\text{ Encuentre todas las funciones diferenciables }}y(t){\text{ tal que}} \hfill \\<br /> y'(t) + y(t) = 2e^t {\text{ y ademas }}y(0) = 1 \hfill \\<br /> \hfill \\ <br />\end{gathered} <br />\]<br />$ $TEX: \[<br />\begin{gathered}<br /> 2.{\text{ Sea }}y(t){\text{ una funcion tal que }}y'(t) - y(t) = \sinh (t){\text{ y ademas }}y(0) = 0.{\text{ Determine}} \hfill \\<br /> {\text{el valor de la decima derivada de }}y{\text{ en cero}} \hfill \\ <br />\end{gathered} <br />\]<br />$ $TEX: \[<br />\begin{gathered}<br /> \boxed{{\text{Control 13}}} \hfill \\<br /> \hfill \\<br /> 1.{\text{ Encuentre la ecuacion de la elipse que tiene focos en }}\left( {4,2} \right) \wedge \left( { - 4,2} \right){\text{ y uno de}} \hfill \\<br /> {\text{sus vertices es }}\left( {6,2} \right) \hfill \\<br /> \hfill \\<br /> 2.{\text{ Considera el conjunto de puntos P cuya distancia al eje X es igual a su distancia}} \hfill \\<br /> {\text{al punto }}\left( {0, - 2} \right).{\text{ Si es una conica}}{\text{, encuentra su ecuacion cartesiana y sus vertices}} \hfill \\<br /> \hfill \\<br /> \boxed{{\text{Control 14}}} \hfill \\<br /> \hfill \\<br /> 1.{\text{ Encuentre los valores de }}a{\text{ que hacen que el sistema tenga solucion no vacia}} \hfill \\<br /> \left. {\underline {\, <br /> \begin{gathered}<br /> 2x - y + z = 3 \hfill \\<br /> 5x - 3y + z = 0 \hfill \\<br /> 3x - 2y = a \hfill \\ <br />\end{gathered} \,}}\! \right\| \hfill \\<br /> \hfill \\<br /> 2.{\text{ Encuentre todas las matrices que conmutan con }}\left( {\begin{array}{*{20}c}<br /> {\text{1}} & {\text{1}} \\<br /> 0 & { - 1} \\<br /><br /> \end{array} } \right) \hfill \\ <br />\end{gathered} <br />\]<br />$ Toda esta materia se vio de manera muy general, asi que como veran, los controles no estan nada de dificiles... y no hay mas, por fin Las indicaciones son las mismas de siempre -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti $TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />$

Jean Renard Gran... Jean Renard Granier Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 22 2008, 01:39 AM Publicado: #2
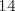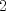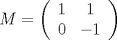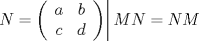Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.920 Registrado: 19-August 06 Desde: DIM, DCC Beauchef Miembro Nº: 1.989 Nacionalidad: Universidad: Sexo:	Control $TEX: $$14$$$ Pregunta $TEX: $$2$$$ Dada la matriz $TEX: $$M = \left( {\begin{array}{{20}c}<br /> 1 & 1 \\<br /> 0 & { - 1} \\<br /><br /> \end{array} } \right)$$$ , queremos encontrar una matriz $TEX: $$\left. 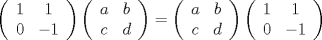{N = \left( {\begin{array}{{20}c}<br /> a & b \\<br /> c & d \\<br /><br /> \end{array} } \right)} \right\|MN = NM$$$ $TEX: $$\left( {\begin{array}{{20}c}<br /> 1 & 1 \\<br /> 0 & { - 1} \\<br /><br /> \end{array} } \right)\left( {\begin{array}{{20}c}<br /> a & b \\<br /> c & d \\<br /><br /> \end{array} } \right) = \left( {\begin{array}{{20}c}<br /> a & b \\<br /> c & d \\<br /><br /> \end{array} } \right)\left( {\begin{array}{{20}c}<br /> 1 & 1 \\<br /> 0 & { - 1} \\<br /><br /> \end{array} } \right)$$$ $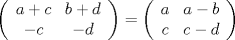TEX: $$\left( {\begin{array}{{20}c}<br /> {a + c} & {b + d} \\<br /> { - c} & { - d} \\<br /><br /> \end{array} } \right) = \left( {\begin{array}{{20}c}<br /> a & {a - b} \\<br /> c & {c - d} \\<br /><br /> \end{array} } \right)$$$ $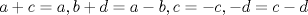TEX: $$a + c = a,b + d = a - b,c = - c, - d = c - d$$$ $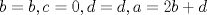TEX: $$b = b,c = 0,d = d,a = 2b + d$$$ $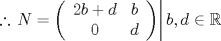TEX: $$\therefore \left. {N = \left( {\begin{array}{{20}c}<br /> {2b + d} & b \\<br /> 0 & d \\<br /><br /> \end{array} } \right)} \right\|b,d \in \mathbb{R}$$$ Suerte en los últimos días. Mensaje modificado por neo shykerex* el Nov 22 2008, 01:42 AM -------------------- Miembro de Anime No Seishin Doukokai, podrías ser el próximo.

LanderGuitar Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 23 2008, 07:36 AM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 568 Registrado: 8-July 08 Desde: Rancagua Miembro Nº: 29.447 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \[<br />\begin{gathered}<br /> \boxed{{\text{Control 12}}} \hfill \\<br /> \left. 1 \right) \hfill \\ <br />\end{gathered} <br />\]$ $TEX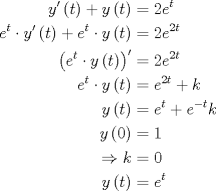: <br />\begin{equation}<br />\begin{aligned}<br /> y'\left( t \right) + y\left( t \right) &= 2e^t \\ <br /> e^t \cdot y'\left( t \right) + e^t \cdot y\left( t \right) &= 2e^{2t} \\ <br /> \left( {e^t \cdot y\left( t \right)} \right)' &= 2e^{2t} \\ <br /> e^t \cdot y\left( t \right) &= e^{2t} + k \\ <br /> y\left( t \right) &= e^t + e^{ - t} k \\ <br /> y\left( 0 \right) &= 1 \\ <br /> \Rightarrow k &= 0 \\ <br /> y\left( t \right) &= e^t \\ <br />\end{aligned}<br />\end{equation}<br />$ $TEX: \[<br />\begin{gathered}<br /> \left. 2 \right) \hfill \\ <br />\end{gathered} <br />\]$ $TEX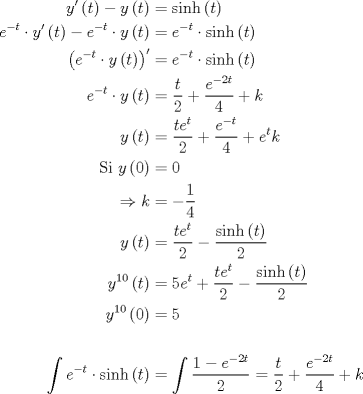: \begin{equation}<br />\begin{aligned}<br /> y'\left( t \right) - y\left( t \right) &= \sinh \left( t \right) \hfill \\<br /> e^{ - t} \cdot y'\left( t \right) - e^{ - t} \cdot y\left( t \right) &= e^{ - t} \cdot \sinh \left( t \right) \hfill \\<br /> \left( {e^{ - t} \cdot y\left( t \right)} \right)' &= e^{ - t} \cdot \sinh \left( t \right) \hfill \\<br /> e^{ - t} \cdot y\left( t \right) &= \frac{t}<br />{2} + \frac{{e^{ - 2t} }}<br />{4} + k \hfill \\<br /> y\left( t \right) &= \frac{{te^t }}<br />{2} + \frac{{e^{ - t} }}<br />{4} + e^t k \hfill \\<br /> {\text{Si }}y\left( 0 \right) &= 0 \hfill \\<br /> \Rightarrow k &= - \frac{1}<br />{4} \hfill \\<br /> y\left( t \right) &= \frac{{te^t }}<br />{2} - \frac{{\sinh \left( t \right)}}<br />{2} \hfill \\<br /> y^{10} \left( t \right) &= 5e^t + \frac{{te^t }}<br />{2} - \frac{{\sinh \left( t \right)}}<br />{2} \hfill \\<br /> y^{10} \left( 0 \right) &= 5 \hfill \\ <br /> \hfill \\<br /> \int {e^{ - t} \cdot \sinh \left( t \right)} &= \int {\frac{{1 - e^{ - 2t} }}<br />{2}} = \frac{t}<br />{2} + \frac{{e^{ - 2t} }}<br />{4} + k \hfill \\<br /> \hfill \\<br />\end{aligned}<br />\end{equation}$ Si estoy mal... me agarran a chuchadas no más. xD! Mensaje modificado por LanderGuitar el Nov 23 2008, 07:36 AM -------------------- $TEX: Educación 2020$ El 2% de los adolescentes no han fumado , si eres del "penoso" 98% que lo ha hecho, copia y pega esto en tu firma.

LanderGuitar Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 23 2008, 09:02 AM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 568 Registrado: 8-July 08 Desde: Rancagua Miembro Nº: 29.447 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \[<br />\begin{gathered}<br /> F_1 = \left( {4,2} \right) \hfill \\<br /> F_2 = \left( { - 4,2} \right) \hfill \\<br /> V_a = \left( {6,2} \right) \hfill \\<br /> V_b = \left( {x_0 ,y_0 } \right) \hfill \\<br /> {\text{Como podemos notar}}{\text{, el centro de la elipse se encuentra en }}\left( {0,2} \right){\text{.}} \hfill \\<br /> \Rightarrow a = 6 \wedge V_b = \left( {0,y_0 } \right) \hfill \\<br /> \hfill \\<br /> {\text{En la elipse se cumple que:}} \hfill \\<br /> d_{\left( {F_1 ,V_a } \right)} + d_{\left( {F_2 ,V_a } \right)} = k \hfill \\<br /> \sqrt {\left( {4 - 6} \right)^2 + \left( {2 - 2} \right)^2 } + \sqrt {\left( { - 4 - 6} \right)^2 + \left( {2 - 2} \right)^2 } = k \hfill \\<br /> \Rightarrow k = 12 \hfill \\<br /> \hfill \\<br /> {\text{Adem\'as se cumple que:}} \hfill \\<br /> b^2 + 4^2 = 6^2 \hfill \\<br /> \Rightarrow b = 2\sqrt 5 \hfill \\<br /> \hfill \\<br /> \therefore {\text{La ecuaci\'on cartesiana de la elipse ser\'a :}} \hfill \\<br /> \frac{{\left( x \right)^2 }}<br />{{\left( 6 \right)^2 }} + \frac{{\left( {y - 2} \right)^2 }}<br />{{\left( {2\sqrt 5 } \right)^2 }} = 1 \hfill \\ <br />\end{gathered} <br />\]<br />$ Mensaje modificado por LanderGuitar el Nov 23 2008, 09:03 AM Archivo(s) Adjunto(s) Elipse.png ( 22.24k ) Número de descargas: 6 -------------------- $TEX: Educación 2020$ El 2% de los adolescentes no han fumado , si eres del "penoso" 98% que lo ha hecho, copia y pega esto en tu firma.

LanderGuitar Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 23 2008, 09:22 AM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 568 Registrado: 8-July 08 Desde: Rancagua Miembro Nº: 29.447 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Y en la 1 del control 14, llego a que a=-3. D: Y en la 2 del control 11, llego a e. Mensaje modificado por LanderGuitar el Nov 23 2008, 09:34 AM -------------------- $TEX: Educación 2020$ El 2% de los adolescentes no han fumado , si eres del "penoso" 98% que lo ha hecho, copia y pega esto en tu firma.

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 23 2008, 09:34 AM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(naxoobkn @ Nov 21 2008, 10:39 PM) $TEX: \[<br />\begin{gathered}<br /> \boxed{{\text{Control 11}}} \hfill \\<br /> 2.{\text{ Determine el radio de convergencia de la serie }}\sum\limits_{n = 0}^\infty {\frac{{n!x^n }}<br />{{n^n }}} \hfill \\<br /> \hfill \\<br />\end{gathered} <br />\]<br />$ 1b) -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

LanderGuitar Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 23 2008, 10:04 AM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 568 Registrado: 8-July 08 Desde: Rancagua Miembro Nº: 29.447 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	No estaba tan lejos por lo menos. xD! -------------------- $TEX: Educación 2020$ El 2% de los adolescentes no han fumado , si eres del "penoso" 98% que lo ha hecho, copia y pega esto en tu firma.

Naxoo Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 23 2008, 10:47 AM Publicado: #8
Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Muy bien LanderGuitar todas tus respuestas son correctas! aunque esto: CITA(LanderGuitar @ Nov 23 2008, 10:22 AM) en la 1 del control 14, llego a que a=-3. Y en la 2 del control 11, llego a e. deberias fundamentarlo un poco mas, pero como estamos en fmat y no dando el control, da lo mismo xD Lo que si me gustaria saber, en el control 12, en la pregunta 2, es como llegaste tan facil la decima derivata de y(t) CITA(Abu-Khalil @ Nov 23 2008, 10:34 AM) 1b) jaja si, cuando lo vi me acorde de tu control, pero igual hice la otra del control 11... no se por que xD -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti $TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />$

LanderGuitar Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 23 2008, 12:27 PM Publicado: #9
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 568 Registrado: 8-July 08 Desde: Rancagua Miembro Nº: 29.447 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(naxoobkn @ Nov 23 2008, 11:47 AM) Muy bien LanderGuitar todas tus respuestas son correctas! aunque esto: deberias fundamentarlo un poco mas, pero como estamos en fmat y no dando el control, da lo mismo xD Lo que si me gustaria saber, en el control 12, en la pregunta 2, es como llegaste tan facil la decima derivata de y(t) jaja si, cuando lo vi me acorde de tu control, pero igual hice la otra del control 11... 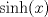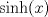no se por que xD Cada vez que se derive "parmente" $TEX: sinh$(x)$$ , dará el mismo $TEX: sinh$(x)$$ . 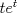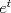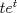Cada 2 veces que derive $TEX: $te^{t}$$ , aparece un $TEX: $e^{t}$$ y queda el mismo $TEX: $te^{t}$$ . 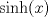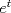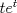Entonces, como se derivó 10 veces, nos queda el $TEX: sinh$(x)$$ y 5 veces el $TEX: $e^{t}$$ y quedó el mismo $TEX: $te^{t}$$ . Eso. 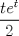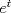=B EDIT: $TEX: $\displaystyle \frac{te^{t}}{2}$$ , el hecho de que esté dividido por 2, es la razón de que cada 2 veces aparezca el $TEX: $e^{t}$$ . Mensaje modificado por LanderGuitar el Nov 23 2008, 12:32 PM -------------------- $TEX: Educación 2020$ El 2% de los adolescentes no han fumado , si eres del "penoso" 98% que lo ha hecho, copia y pega esto en tu firma.

LanderGuitar Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 23 2008, 01:10 PM Publicado: #10
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 568 Registrado: 8-July 08 Desde: Rancagua Miembro Nº: 29.447 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Lo hice así yo: $TEX: \[<br />\begin{gathered}<br /> \boxed{{\text{Control 14}}} \hfill \\<br /> \left. 1 \right) \hfill \\<br /> 2x - y + z = 3 \hfill \\<br /> 5x - 3y + z = 0 \hfill \\<br /> 3x - 2y = a \hfill \\<br /> {\text{Convirtiendo a matriz el sistema:}} \hfill \\<br /> \left( {\begin{array}{{20}c}<br /> 2 & { - 1} & 1 \\<br /> 5 & { - 3} & 1 \\<br /> 3 & { - 2} & 0 \\<br /><br /> \end{array} } \right)\left( {\begin{array}{{20}c}<br /> x \\<br /> y \\<br /> z \\<br /><br /> \end{array} } \right) = \left( {\begin{array}{{20}c}<br /> 3 \\<br /> 0 \\<br /> a \\<br /><br /> \end{array} } \right) \hfill \\<br /> \left( {\left. {\begin{array}{{20}c}<br /> 2 & { - 1} & 1 \\<br /> 5 & { - 3} & 1 \\<br /> 3 & { - 2} & 0 \\<br /><br /> \end{array} } \right\|\begin{array}{{20}c}<br /> 3 \\<br /> 0 \\<br /> a \\<br /><br /> \end{array} } \right)\widetilde{F_2 - F_1 }\left( {\left. {\begin{array}{{20}c}<br /> 2 & { - 1} & 1 \\<br /> 3 & { - 2} & 0 \\<br /> 3 & { - 2} & 0 \\<br /><br /> \end{array} } \right\|\begin{array}{{20}c}<br /> 3 \\<br /> { - 3} \\<br /> a \\<br /><br /> \end{array} } \right) \hfill \\<br /> \widetilde{F_3 - F_2 }\left( {\left. {\begin{array}{{20}c}<br /> 2 & { - 1} & 1 \\<br /> 3 & { - 2} & 0 \\<br /> 0 & 0 & 0 \\<br /><br /> \end{array} } \right\|\begin{array}{{20}c}<br /> 3 \\<br /> { - 3} \\<br /> {a + 3} \\<br /><br /> \end{array} } \right) \hfill \\<br /> {\text{Si }}a \ne - 3,{\text{ el sistema no tiene soluci\'on}}{\text{. }} \hfill \\<br /> {\text{Si }}a = - 3: \hfill \\<br /> \widetilde{F_2 - 2F_1 }\left( {\left. {\begin{array}{{20}c}<br /> 2 & { - 1} & 1 \\<br /> { - 1} & 0 & 2 \\<br /><br /> \end{array} } \right\|\begin{array}{{20}c}<br /> 3 \\<br /> { - 9} \\<br /><br /> \end{array} } \right)\widetilde{F_1 + 2F_2 }\left( {\left. {\begin{array}{{20}c}<br /> 0 & { - 1} & 5 \\<br /> { - 1} & 0 & 2 \\<br /><br /> \end{array} } \right\|\begin{array}{{20}c}<br /> { - 15} \\<br /> { - 9} \\<br /><br /> \end{array} } \right)\begin{array}{{20}c}<br /> {\widetilde{ - F_1 }} \\<br /> {\widetilde{ - F_2 }} \\<br /><br /> \end{array} \left( {\left. {\begin{array}{{20}c}<br /> 0 & 1 & { - 5} \\<br /> 1 & 0 & { - 2} \\<br /><br /> \end{array} } \right\|\begin{array}{{20}c}<br /> {15} \\<br /> 9 \\<br /><br /> \end{array} } \right) \hfill \\<br /> {\text{El sistema tiene infinitas soluciones si:}} \hfill \\<br /> y = 5z + 15 \hfill \\<br /> x = 2z + 9 \hfill \\ <br />\end{gathered} <br />\]<br />$ -------------------- $TEX: Educación 2020$ El 2% de los adolescentes no han fumado , si eres del "penoso" 98% que lo ha hecho, copia y pega esto en tu firma.

« Posterior · Matemáticas 2 · Anterior »

3 Páginas:

1 2 3 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 05:23 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.