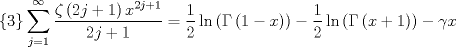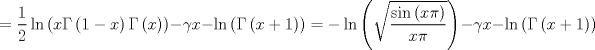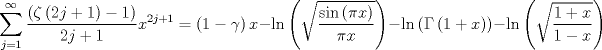|
|
|
|
|
|
|
  |
 Nov 19 2008, 01:08 AM Nov 19 2008, 01:08 AM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.920 Registrado: 19-August 06 Desde: DIM, DCC Beauchef Miembro Nº: 1.989 Nacionalidad:  Universidad:  Sexo:  |
Probar que
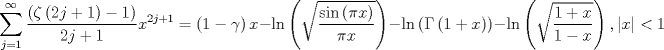 . .Mensaje modificado por neo shykerex el Nov 19 2008, 10:44 AM -------------------- Miembro de Anime No Seishin Doukokai, podrías ser el próximo.
|
|
|
|
 Mar 14 2010, 12:55 PM Mar 14 2010, 12:55 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.313 Registrado: 28-June 07 Miembro Nº: 7.123 Nacionalidad:  Colegio/Liceo:  Sexo:  |
-------------------- Hay dos cosas infinitas: el Universo y la estupidez humana. Y del Universo no estoy seguro
|
|
|
|
 Mar 16 2010, 10:34 AM Mar 16 2010, 10:34 AM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.920 Registrado: 19-August 06 Desde: DIM, DCC Beauchef Miembro Nº: 1.989 Nacionalidad:  Universidad:  Sexo:  |
Correcto, pasar a resueltos.
-------------------- Miembro de Anime No Seishin Doukokai, podrías ser el próximo.
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 09:24 PM |








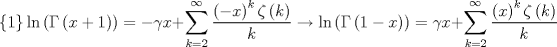
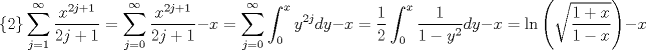
![TEX: $$\sum\limits_{j=2}^{\infty }{\frac{\left[ 1-\left( -1 \right)^{n} \right]\zeta \left( j \right)x^{j}}{j}}=2\sum\limits_{j=1}^{\infty }{\frac{\zeta \left( 2j+1 \right)x^{2j+1}}{2j+1}}$$](./tex/7d27b9e138df88dbe18ca50913c55814.png)