 1080 |
|
|
|
|
|
|
Foro fmat.cl > Sector Preparación PSU - Construyendo tu camino al éxito !! > Consultas > Banco de Problemas Resueltos > Resueltos de Álgebra y Funciones  |
 Jul 19 2006, 01:22 PM
Publicado:
#1
|
|
 Dios Matemático  Grupo: Usuario FMAT Mensajes: 309 Registrado: 12-February 06 Desde: Santiago Miembro Nº: 566 Nacionalidad:  Universidad:  Sexo:   |
Pauta: D.
Me da la D, pero con los signos del exponente cambiados.
Archivo(s) Adjunto(s)
|
 |
 
|
|
Jul 19 2006, 02:52 PM
Publicado:
#2
|
|
 Staff FMAT  Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad: Sexo:  |
![TEX: \[<br />\begin{gathered}<br /> \left[ {\left( {a^{x + 1} } \right)^x \div \left( {a^{x - 1} } \right)^x } \right] \cdot \left( {a^{1 - x} } \right)^{x - 1} = \frac{{\left( {a^{x + 1} } \right)^x }}<br />{{\left( {a^{x - 1} } \right)^x }} \cdot \left( {a^{1 - x} } \right)^{x - 1} \hfill \\<br /> \left[ {\left( {a^{x + 1} } \right)^x \div \left( {a^{x - 1} } \right)^x } \right] \cdot \left( {a^{1 - x} } \right)^{x - 1} = \left( {a^{x + 1 - (x - 1)} } \right)^x \cdot \left( {a^{1 - x} } \right)^{x - 1} \hfill \\<br /> \left[ {\left( {a^{x + 1} } \right)^x \div \left( {a^{x - 1} } \right)^x } \right] \cdot \left( {a^{1 - x} } \right)^{x - 1} = \left( {a^{x + 1 - x + 1} } \right)^x \cdot \left( {a^{1 - x} } \right)^{x - 1} \hfill \\<br /> \left[ {\left( {a^{x + 1} } \right)^x \div \left( {a^{x - 1} } \right)^x } \right] \cdot \left( {a^{1 - x} } \right)^{x - 1} = \left( {a^2 } \right)^x \cdot a^{ - (x^2 - 2x + 1)} \hfill \\<br /> \left[ {\left( {a^{x + 1} } \right)^x \div \left( {a^{x - 1} } \right)^x } \right] \cdot \left( {a^{1 - x} } \right)^{x - 1} = a^{2x} \cdot a^{ - (x^2 - 2x + 1)} \hfill \\<br /> \left[ {\left( {a^{x + 1} } \right)^x \div \left( {a^{x - 1} } \right)^x } \right] \cdot \left( {a^{1 - x} } \right)^{x - 1} = a^{2x - x^2 + 2x - 1} \hfill \\<br /> \left[ {\left( {a^{x + 1} } \right)^x \div \left( {a^{x - 1} } \right)^x } \right] \cdot \left( {a^{1 - x} } \right)^{x - 1} = a^{4x - 1 - x^2 } \hfill \\ <br />\end{gathered} <br />\]](./tex/93051.gif) Concuerdo contigo, entonces la e). 
|
|
|
|
|
Jul 19 2006, 02:53 PM
Publicado:
#3
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 120 Registrado: 16-May 06 Desde: Concepción Miembro Nº: 1.106 Nacionalidad: Sexo: |
![TEX: % MathType!MTEF!2!1!+-<br />% feqaeaartrvr0aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaebbnrfifHhDYfgasaacH8srps0l<br />% bbf9q8WrFfeuY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0R<br />% Yxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGa<br />% caGaaeqabaaaamaaaOabaeqabaWaaeWaaeaadaWcaaqaamaabmaaba<br />% GaamyyamaaCaaaleqabaGaamiEaiabgUcaRiaaigdaaaaakiaawIca<br />% caGLPaaadaahaaWcbeqaaiaadIhaaaaakeaadaqadaqaaiaadggada<br />% ahaaWcbeqaaiaadIhacqGHsislcaaIXaaaaaGccaGLOaGaayzkaaWa<br />% aWbaaSqabeaacaWG4baaaaaaaOGaayjkaiaawMcaaiabgwSixpaabm<br />% aabaGaamyyamaaCaaaleqabaGaaGymaiabgkHiTiaadIhaaaaakiaa<br />% wIcacaGLPaaadaahaaWcbeqaaiaadIhacqGHsislcaaIXaaaaaGcba<br />% aabaGaeyypa0ZaaeWaaeaacaWGHbWaaWbaaSqabeaacaWG4bGaey4k<br />% aSIaaGymaiabgkHiTiaadIhacqGHRaWkcaaIXaaaaaGccaGLOaGaay<br />% zkaaGaeyyXICTaaiikaiaadggacaGGPaWaaWbaaSqabeaacqGHsisl<br />% caWG4bWaaWbaaWqabeaacaaIYaaaaSGaey4kaSIaaGOmaiaadIhacq<br />% GHsislcaaIXaaaaOGaeyypa0JaamyyamaaCaaaleqabaGaaGOmaiaa<br />% dIhaaaGccqGHflY1caWGHbWaaWbaaSqabeaacqGHsislcaWG4bWaaW<br />% baaWqabeaacaaIYaaaaSGaey4kaSIaaGOmaiaadIhacqGHsislcaaI<br />% XaaaaaGcbaaabaGaeyypa0JaamyyamaaCaaaleqabaGaeyOeI0Iaam<br />% iEamaaCaaameqabaGaaGOmaaaaliabgUcaRiaaisdacaWG4bGaeyOe<br />% I0IaaGymaaaaaaaa!77FC!<br />\[<br />\begin{gathered}<br /> \left( {\frac{{\left( {a^{x + 1} } \right)^x }}<br />{{\left( {a^{x - 1} } \right)^x }}} \right) \cdot \left( {a^{1 - x} } \right)^{x - 1} \hfill \\<br /> \hfill \\<br /> = \left( {a^{x + 1 - x + 1} } \right) \cdot (a)^{ - x^2 + 2x - 1} = a^{2x} \cdot a^{ - x^2 + 2x - 1} \hfill \\<br /> \hfill \\<br /> = a^{ - x^2 + 4x - 1} \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/93052.gif) eeeeeeeeeeeee -------------------- Todos los hombres son sabios; unos antes, los otros, después.(Goethe)
|
|
|
|
|
Jul 19 2006, 02:55 PM
Publicado:
#4
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 120 Registrado: 16-May 06 Desde: Concepción Miembro Nº: 1.106 Nacionalidad: Sexo: |
  otra vez krizalid 
-------------------- Todos los hombres son sabios; unos antes, los otros, después.(Goethe)
|
|
|
|
|
Jul 19 2006, 04:29 PM
Publicado:
#5
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 309 Registrado: 12-February 06 Desde: Santiago Miembro Nº: 566 Nacionalidad: Universidad: Sexo: |
Jaja, pero si fue por 1 minuto no más. Gracias a los dos
|
|
|
|
|
Jul 19 2006, 06:40 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.352 Registrado: 5-October 05 Miembro Nº: 330 Nacionalidad: Universidad:  Sexo: |
Veamos otra forma:
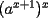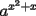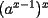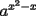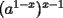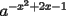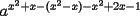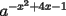 =   =   =  Como tenemos multiplicacíon y division de potencias de igual base, las podemos expresar en una sola potencia, a saber:  , finalmente tenemos Saludos y mis congratulaciones, pero una vez que saques un problema, gasta tiempo en buscar otro forma ojalá más elegante, esta es una muy buena forma de estudiar. 
-------------------- |
|
|
|
|
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 09:23 PM |
