|
|
|
|
|
|
|
  |
 Jul 14 2005, 06:50 PM Jul 14 2005, 06:50 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Comienzo con la lista de siete problemas de esta semana... tengan algo de cuidado, los problemas podrían no ser tan fáciles.
Problema 1: Sea 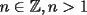 (fijo), y sean (fijo), y sean 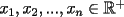 cualesquiera. Definiremos una función cualesquiera. Definiremos una función 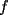 que hace lo siguiente: toma que hace lo siguiente: toma  números reales y arma todos los productos posibles entre dos de ellos, y luego suma estos productos. Por ejemplo: números reales y arma todos los productos posibles entre dos de ellos, y luego suma estos productos. Por ejemplo:Si 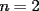 , entonces , entonces 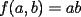 Si 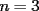 , entonces , entonces 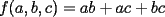 Si 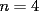 , entonces , entonces 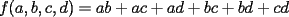 y así sucesivamente Determine la mayor constante 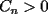 que cumple la siguiente propiedad: que cumple la siguiente propiedad: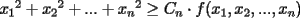 , para todo , para todo 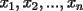 en las condiciones del problema en las condiciones del problemaPara el valor de 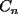 que usted haya encontrado, determine condiciones necesarias y suficientes que establezcan la igualdad. que usted haya encontrado, determine condiciones necesarias y suficientes que establezcan la igualdad.Mi única sugerencia es que estudien los casos 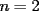 y y 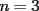 (que son bien conocidos). Luego podrá darse cuenta de lo que usted necesita para resolver el caso general. Este problema va con cariño para mis alumnos que fueron el Sábado a entrenamiento, este es mi problema relacionado con lo visto en clases. (que son bien conocidos). Luego podrá darse cuenta de lo que usted necesita para resolver el caso general. Este problema va con cariño para mis alumnos que fueron el Sábado a entrenamiento, este es mi problema relacionado con lo visto en clases.
-------------------- |
|
|
|
 Jul 14 2005, 06:55 PM Jul 14 2005, 06:55 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Ahora viene una tierna historia de familia (bueno ya... tal vez de tierna tiene poco, eso lo deciden ustedes), la dificultad es de olimpiada nacional, con suerte, sólo que en otro contexto. Este es el...
Problema 2: La madre de Antonia compró, para su hija, muchas canicas gigantes, cada una de ellas con 10 cm de radio (las compró de este tamaño para que Antonia, de 2 años, no se las tragara). Su hermano Sebastián quiso diseñar una caja de 20 cm de alto, 160 cm de largo y 1 m de ancho, para así guardar estas canicas, y su padre le compró los materiales y le prestó las herramientas. Mientras construía esta caja con sus otras hermanas, una de ellas preguntó a Sebastián: "¿Cuál es el mayor número de canicas que pueden ser puestas en esta caja?" Sebastián no quiso contestar esa pregunta... sabía que su hermana (de 14 años y sin mucha preparación matemática) iba a hallar de manera inconciente dicho valor. ¿Puede usted hallar ese valor máximo? Por favor justificar su respuesta, para que la hermana de Sebastián pueda entenderlo. -------------------- |
|
|
|
| Corecrasher |
 Jul 14 2005, 07:46 PM Jul 14 2005, 07:46 PM
Publicado:
#3
|
|
Invitado |
2) Fijémonos que es una caja de 20 cm de alto, 160 cm de largo y 1 m de ancho , a su vez notemos que tienen radio 10cm , ósea diámetro 20cm , la idea es para que sea el máximo dejarlas lo mas pegaditas posibles. Igualmente notemos que el alto es 20cm , lo que es el diámetro , así que no podremos montarlas , solo abra una por vez. , a lo largo habrán 8 ya que 8*20=160 y a lo ancho 5 ya que 20cm*5=1m. Multiplicando 8*5 , concluimos que podremos poner como máximo 40 canicas GIGANTESCAS , buscare para encontrar alguna algun dia.
|
|
|
|
| Corecrasher |
 Jul 14 2005, 09:38 PM Jul 14 2005, 09:38 PM
Publicado:
#4
|
|
Invitado |
Propuesto 3:
Sobre un triángulo rectángulo de papel, se han pintado dos puntos A y B. Usted dispone de una tijera y tiene derecho a realizar cortes (sobre el papel) de la siguiente forma: cortar a través de una altura del triángulo dado. Al hacerlo retira, sin la respectiva altura, uno de los dos triángulos y continua el proceso. Demuestre que después de un número finito de cortes Usted puede separar los puntos A y B dejando uno de ellos fuera de los triángulos que permanecen. |
|
|
|
 Jul 14 2005, 09:49 PM Jul 14 2005, 09:49 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Corecrasher, como decía al proponer el problema 2, encontrar intuitivamente la solución correcta es fácil (o sea en este problema les he tirado algo de ayuda), pero no has argumentado por qué es óptima. Muy bien al explicar que las canicas gigantes (para que la Antonia no se las trague) no pueden montarse. Fíjate que si disponemos las canicas y hacemos un corte a la caja, paralelo a las caras de 100 cm×160 cm, y a 10 cm. de altura, el problema se traduce a disponer circunferencias en un rectángulo, donde ellas pueden tener 0 puntos en común, o a lo más ser tangentes.
Muy bien lo que pusiste, 40 es el óptimo. Lo que queda es probar que no se pueden colocar 41. En esto te puede servir de ayuda esa visión bidimensional del problema -------------------- |
|
|
|
 Jul 14 2005, 10:24 PM Jul 14 2005, 10:24 PM
Publicado:
#6
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 293 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 3 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Aqui va la solucion para el problema 1
 Eso es , ojala este buena y que se entienda Saludos --------------------  |
|
|
|
| Corecrasher |
 Jul 14 2005, 10:47 PM Jul 14 2005, 10:47 PM
Publicado:
#7
|
|
Invitado |
CITA(xsebastian) Corecrasher, como decía al proponer el problema 2, encontrar intuitivamente la solución correcta es fácil (o sea en este problema les he tirado algo de ayuda), pero no has argumentado por qué es óptima. Muy bien al explicar que las canicas gigantes (para que la Antonia no se las trague) no pueden montarse. Fíjate que si disponemos las canicas y hacemos un corte a la caja, paralelo a las caras de 100 cm×160 cm, y a 10 cm. de altura, el problema se traduce a disponer circunferencias en un rectángulo, donde ellas pueden tener 0 puntos en común, o a lo más ser tangentes.
Muy bien lo que pusiste, 40 es el óptimo. Lo que queda es probar que no se pueden colocar 41. en esto te puede servir de ayuda esa visión bidimensional del problema Es que mi argumento es por que las pongo lo mas apretaditas posibles (TANGENTES), por lo cual no podrian ser 41... |
|
|
|
 Jul 14 2005, 10:50 PM Jul 14 2005, 10:50 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
CITA(Corecrasher) Es que mi argumento es por que las pongo lo mas apretaditas posibles (TANGENTES), por lo cual no podrian ser 41... Pero tú sabes que con ese argumento no convences a un corrector de olimpiada, ni siquiera a uno de campeonato escolar. No veo un argumento en tus palabras, o sea yo podría ponerlas apretaditas de otro modo y tal vez quepan más. La tarea es ver por qué (sin importar de qué manera espacial trate de apretarlas) no puedo colocar 41 -------------------- |
|
|
|
 Jul 14 2005, 10:54 PM Jul 14 2005, 10:54 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
La solución de Caetano está buena. Agregaré, como comentario, que
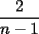 es la mayor constante que uno puede elegir. De hecho, cuando uno toma todos los valores iguales, entonces se hace evidente que no puedo colocar una mayor. es la mayor constante que uno puede elegir. De hecho, cuando uno toma todos los valores iguales, entonces se hace evidente que no puedo colocar una mayor.Comparto con ustedes otra solución, que puede obtenerse con la desigualdad entre la media aritmética y la media cuadrática, luego de elevarla al cuadrado. Esto nos lleva a lo siguiente: 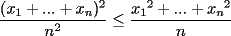 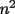 para obtener la siguiente desigualdad (que también puede ser obtenida gracias a la desigualdad de Cauchy-Schwarz): para obtener la siguiente desigualdad (que también puede ser obtenida gracias a la desigualdad de Cauchy-Schwarz):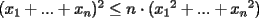 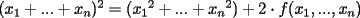 , y con un poco de aritmética llegamos a lo pedido. Las condiciones de igualdad también se obtienen del mismo modo... , y con un poco de aritmética llegamos a lo pedido. Las condiciones de igualdad también se obtienen del mismo modo...
-------------------- |
|
|
|
 Jul 14 2005, 11:13 PM Jul 14 2005, 11:13 PM
Publicado:
#10
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 293 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 3 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 4:
Sean tres puntos A, B y C perteneciente a una circunferencia de centro O tales que <AOB es menor que <BOC. Sea D el punto medio del arco AC que contiene a B. Sea K el pie de la perpendicular a BC por D. Pruebe que AB + BK = KC. Saludos a todos --------------------  |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 10:08 PM |








