Primer y Segundo Nivel Grupal Opciones

[felipe_contreras...]

El juego no eléctronico favorito de Mauricio y Loretta, además de entretenido es bastante sabroso de jugar. Se juega de la siguiente manera:

Al principio del juego Mauricio y Loretta construyeron dos columnas de fichas, cada una con un número al azar de fichas en ellas. En cada "movida", el jugador de turno puede o bien retirar cierto número de fichas de una columna, o bien retirar el mismo número de fichas de ambas columnas. Pierde aquel jugador que se queda sin fichas para retirar. Gana el otro jugador.

Este juego fue conocido en China como tsyan-shidzi ("eligiendo piedras"). Luego fue reinventado por el matemático alemán Willem Abraham Wythoff (1865-1939), quién publicó un completo análisis del juego en el año 1907. Una de sus principales ideas era pensar cada partida desde el final hacia el principio. Medio siglo después (alrededor de 1960) y sin percatarse de esto, el matemático Rufud P. Isaacs (de la Universidad Johns Hopkins) dio una versión equivalente del juego en un tablero de ajedrez en términos del movimiento de una Reina. Mauricio y Loretta juegan quitando donas desde dos cajas (cada vez desde sólo una caja o el mismo número de donas de ambas cajas). Demás está decir que ellos son expertos jugadores y siempre llevan a cabo la mejor jugada posible.

Problema 1.Explique por qué si un jugador eventualmente logra dejar una caja con una dona y la otra con dos donas, entonces siempre ganará ese juagador, independientemente de qué jugada realice su contrincante.

Problema 2. Hace unos días Mauricio y Loretta compraron dos cajas de 10 donas cada una, pero una caja traía sólo 9 de ellas. Si Mauricio partió el juego, ¿Quién de ellos ganó finalmente el juego?

Problema 3. Ayer cada uno compró una caja de donas por separardo Loretta compró una caja de 5 donas, pero Mauricio sólo pudo comprar una caja de 3 donas. En esta ocasión Loretta partió el juego argumentando que ella había traído más donas. ¿Quién ganó esta vez?


screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img119.imageshack.us/img119/6241/donuts8om.jpg');}" />


En el año 1960, Rufus P. Isaacs propuso el siguiente juego:

Dos jugadores alternan turnos moviendo una Reina en un tablero de ajedrez de tamaño n x m, ubicada inicialmente en la casilla de abajo y derecha. La Reina puede ser movida en cada jugada sólo hacia arriba, sólo hacia la izquierda o sólo diagonalmente de hacia arriba y la izquierda, pero no hacia abajo ni a la derecha. El ganador del juego es quien posiciona la Reina de la esquina superior izquierda del tablero.

Diremos que una casilla del tablero de n x m es ganadora si cuando a un jugador le toca mover la Reina a partir de dicha casilla siempre puede ganar luego de algunas jugadas, independientemente de cuáles movimientos realice su contrincante. Diremos que una casilla es perdedora si a partir de de ella sólo se puede mover la Reina a casillas ganadoras, por lo que un jugador que parte desde ella siempre perderá el juego si su oponente es suficientemente hábil.

Problema 4. Veamos algunos ejemplos del juego, estudiando las casillas de ciertos tableros. Partimos con un ejemplo:


screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img151.imageshack.us/img151/2820/dibujo9ge.png');}" />


En el tablero de 2 x 2 la casilla superior izquierda la llamamos 1 y seguimos en el orden usual de lectura hastala casilla inferior dercha que es la 4.
La casilla 1 no es ganadora pues si me toca jugar desde allí he perdido. Podemos no catalogarla o catalogarla perdedora. Todas las demás casillas me llevan en un movimento a la casilla superior derecha, luego son ganadoras.

(a) Considere un tablero de 4 x 4. Identifique las casillas gandoras y las perdedoras. Como respuesta debe entregar el tablero con cada casilla marcada con una G o una P indicando respectivamente ganadora o perdedora. Si no puede decidir de qué tipo es una casilla déjela en blanco. Deben justificar todas las marcas hechas sobre el tablero.

(b) Identifique de qué tipo son las casillas de un tablero de 9 x 17. No es necesario justificar en este caso.

A haberse familiarizado con el juego de Isaacs llenando los tableros, seguro se han dado cuenta que no hay casillas en blanco. Esta es una propiedad general.

Problema 5. Explique por qué toda casilla de un tablero de n x m puede ser catalogada o bien como ganadora o bien como perdedora.

Para finalizar esta prueba por equipos, vemos una propiedad muy interesante sobre estos "dos" juegos que hemos presentado.

Problema 6. Justifique la siguiente afirmación (que es cierta) que hizo Loretta luego de conocer el juego de Isaacs:

"El juego de Wythoff y el de Isaccs son en el fondo el mismo juego, yo diría que no hay ninguna diferencia esencial"

Puede servirles como ayuda notar que cada juego tiene tres tipos de jugadas y compararlas.

[Wiccans]

Problema 1:

por que los dos tipos de jugadas que puede realizar el otro jugador son en veneficio al ultimo que jugo...

a) quitar 1 de una columna: dejaria la misma cantidad en ambas columnas por lo cual el otro jugador las limpiaria sacando 1 dona de cada columna

b) quitar 1 de cada columna: una columna desaparece por lo cual el otro jugador solo debe sacar la dona sobrante...


problema 2:

Gana Mauricio. ya que la gran y espectacular jugada es sacar 8 donas de cada columna, haci dejaria una columna con 1 dona y la otra con 2. Y como ya se comprobo anteriormente el gano.

problema 3:

Gano nuevamente Mauricio (es todo un winner mauricio)(o el que hizo la prueba era machista??). puesto que las jugadas "inteligentes" que puede hacer loretta son las siguientes, teniendo en cuenta de que no debe dejar una diferencia de uno puesto ganaria mauricio:

a)emparejar la cantidad (osea 3-3): mauricio ganaria sacando 3 donas de cada lado.

b) sacando 1 o 2 de la columna de 3: mauricio ganaria dejando 2 o 1 respectivamente en la otra columna.

c)sacando 4 de la columna de 5: mauricio ganariadejando 2 en la otra columna.

problema 4:

[Wiccans]

Problema 4:

a)

screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://www.subir-fotos.com/uploads/74f96a5b25.bmp');}" />


G1, G2, G3: se considera ganador por ganar haciendo un movimiento hacia la izquierda.

G4, G5, G6: se considera ganadora por ganar haciendo un movimiento hacia la izquierda.

G7, G9, G13: se considera ganador por ganar haciendo un movimiento diagonalmente.

G8, G10, G11, G12: se considera ganador por ganar haciendo un movimiento a la casilla perdedora mas cercana.

P1, P2: se considera perdedor por solo poder mover a casillas que permiten ganar en un movimiento.

[Wiccans]

Esto no es una bandera ni algo por el estilo... es la solucion segun yo del problema 5


screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://www.subir-fotos.com/uploads/d014d5b0be.bmp');}" />


ahora necesito saber si esta bien... espero sus respuestas...
aunque voy a explicar mejor esto:

las dos casillas perdedores-xtreme son las que estan mas cerca de la meta, despues la diagonal deperdedoras se muestra ya que es donde se debe ir acorralando al otro jugador para que llegue a la casilla perdedor-xtreme, a esta diagonal se puede llegar desde cualquier lugar haci que por eso todas las otrasse marcan con ganadoras.

Esta bien??

despues de pensarlo me di cuenta de que realmente era el meo ...

[Shevchenja]

Respecto al problema 3, yo entiendo tu solución pues a mi esta vez me tocó desarrolar y redactar ese problema, pero creo que deberías redactar tu solución un poco más detallada porque para el que no sabe como es la respuesta, creo que queda un poco colgado jejejeje..
Igual winner Mauricio ^^... no le hizo ninguna gracia a mi compañera de equipo la prueba

Yapos eso, es una critica positiva nomás


Salu2

[tt14123]

Nosotros respondimos asi el :

Supongamos que exite al menos una casilla incatalogable, que no es la superior izquierda, luego:

Caso 1: Si puedes mover la Reina a una casilla considerada Perdedora; entonces tal casilla se catalogará como Ganadora.

Caso 2: Si estas obligado a mover la Reina a una casilla Ganadora, entonces tal casilla se considerara como Perdedora.

Entonces, para que tal casilla sea incatalogable, tendra que poder ser movida a otra casilla incatalogable. Pero para que esta nueva casilla sea incatalogable, tambien debera poder ser movida a otra casilla incatalogable.

Razonando del mismo modo, diremos que la Reina pasara por todo el tablero, tal que todas las casillas seran incatalogables.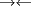



Ya que sabemos que siempre, la casilla de la derecha, la de abajo y/o la inferior derecha a esta, son siempre catalogadas Ganadoras.

SALU

[Animiko]

Esto no es una bandera ni algo por el estilo... es la solucion segun yo del problema 5


screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://www.subir-fotos.com/uploads/d014d5b0be.bmp');}" />


ahora necesito saber si esta bien... espero sus respuestas...
aunque voy a explicar mejor esto:

las dos casillas perdedores-xtreme son las que estan mas cerca de la meta, despues la diagonal deperdedoras se muestra ya que es donde se debe ir acorralando al otro jugador para que llegue a la casilla perdedor-xtreme, a esta diagonal se puede llegar desde cualquier lugar haci que por eso todas las otrasse marcan con ganadoras.

Esta bien??

despues de pensarlo me di cuenta de que realmente era el meo  ...

Está mal pq no puede haber más de una casilla perdedora x diagonal, ya que el resto de la diagonal se consideraría casilla ganadora por tener la posibilidad de mover la reina hacia una casilla perdedora y obligar al otro a perder...
Cuando me pasen el otro PC lo explico mejor con dibujo pq este no tiene naa

[Jaime sscc]

screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img183.imageshack.us/img183/8323/hgfh4qs.jpg');}" />



yap, ahi les dejo la 4 b, ojala no haya un error en el pintado, que arto qeu me costo xD

c'ya

Edited

Condoro, y si no es ahora, nose quepinte mal xD

[S. E. Puelma Moy...]

La última solución publicada, está incorrecta, por favor revisa la definición de casilla perdedora para comprobar

El mensaje que mahuachi había escrito, posterior a este, lo he borrado porque no constituía un real aporte para resolver o comentar esta prueba por equipos. Por el contrario, parecía más bien una burla, hacia un error que cualquiera puede cometer, y no es la idea de FMAT burlarse de los intentos de solución de otros

Así que, a portarse mejor en adelante

[Wiccans]

Esto no es una bandera ni algo por el estilo... es la solucion segun yo del problema 5


screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://www.subir-fotos.com/uploads/d014d5b0be.bmp');}" />


ahora necesito saber si esta bien... espero sus respuestas...
aunque voy a explicar mejor esto:

las dos casillas perdedores-xtreme son las que estan mas cerca de la meta, despues la diagonal deperdedoras se muestra ya que es donde se debe ir acorralando al otro jugador para que llegue a la casilla perdedor-xtreme, a esta diagonal se puede llegar desde cualquier lugar haci que por eso todas las otrasse marcan con ganadoras.

Esta bien??

despues de pensarlo me di cuenta de que realmente era el meo  ...

Verdad!!
esta mal... entonces las unicas casillas perdedoras son las casillas perdedores-xtreme... las dos que estan mas cerca de la casilla final.