Primer Nivel Individual - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > Campeonato Interescolar > Campeonato Interescolar 2006 > Cuarta Fecha

Reply to this topic

Start new topic

Primer Nivel Individual

Killua Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 8 2006, 07:19 PM Publicado: #1
Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \noindent $\boxed{\mathcal{P}_{1}}$ El primer d\'ia de clases en todo colegio significa d\'ia de reencuentros. Se sabe que en un curso de $23$ alumnos hubo $217$ besos en la mejilla para saludarse. 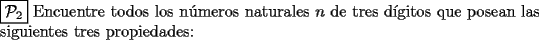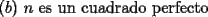Si todo el curso se saluda, ?`Cu\'antos hombres y mujeres tiene el curso?$ $TEX: \noindent $\underline{Nota}$: Los hombres se saludan, entre ellos, s\'olo estrechando sus manos$ $TEX: \noindent $\boxed{\mathcal{P}_{2}}$ Encuentre todos los n\'umeros naturales $n$ de tres d\'igitos que posean las siguientes tres propiedades:$ $TEX: \noindent $(a)$ $n$ es impar$ $TEX: \noindent $(b)$ $n$ es un cuadrado perfecto$ $TEX: \noindent $©$ La suma de los cuadrados de los d\'igitos de $n$ es un cuadrado perfecto.$ Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy) "A mathematician is a device for turning coffee into theorems" (Paul Erdös)

Killua Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 8 2006, 07:28 PM Publicado: #2
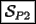Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Para esta pregunta fue muy útil el método zapateñe... 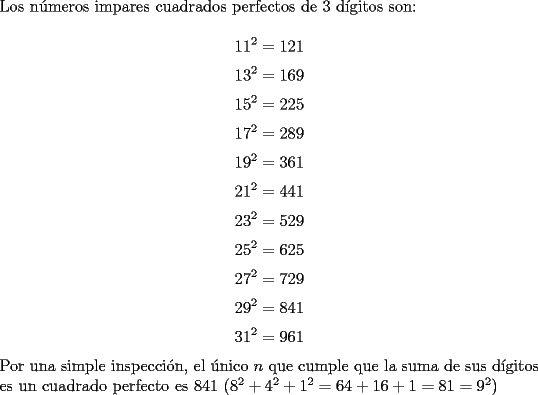$TEX: $\boxed{\mathcal{S}_{P2}}$$ $TEX: \noindent Los n\'umeros impares cuadrados perfectos de $3$ d\'igitos son:<br /><br />$$11^2=121$$<br />$$13^2=169$$<br />$$15^2=225$$<br />$$17^2=289$$<br />$$19^2=361$$<br />$$21^2=441$$<br />$$23^2=529$$<br />$$25^2=625$$<br />$$27^2=729$$<br />$$29^2=841$$<br />$$31^2=961$$<br /><br />\noindent Por una simple inspecci\'on, el \'unico $n$ que cumple que la suma de sus d\'igitos es un cuadrado perfecto es $841$ $(8^2+4^2+1^2=64+16+1=81=9^2)$$ Saludos PD: grande Alemania!!!! -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy) "A mathematician is a device for turning coffee into theorems" (Paul Erdös)

Jaime sscc Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 8 2006, 07:57 PM Publicado: #3
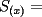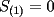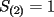Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 167 Registrado: 17-May 05 Desde: Santiago, Chile Miembro Nº: 38 Nacionalidad: Colegio/Liceo: Sexo:	Esta fecha en 2 palabras : Brute Force P1 Analicemos solo a las mujeres: $TEX: $\displaystyle S_{(x)}=$$ Cantidad de saludos solo entre $TEX: $x$$ mujeres $TEX: $\displaystyle S_{(1)}=0$$ $TEX: $\displaystyle S_{(2)}=1$$ $TEX: $\vdots$$ Bueno, pero, es muy atadoso seguir asi, asi que demonos cuenta de lo siguiente, cuando se agrega una mujer,se agregan 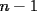$TEX: $n-1$$ saludos a $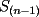TEX: $\displaystyle S_{(n-1)}$$ por ende, $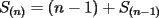TEX: $\displaystyle S_{(n)}=(n-1)+S_{(n-1)}$$ Trabajando la expresion: 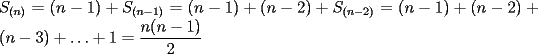$TEX: \noindent$\displaystyle S_{(n)}=(n-1)+S_{(n-1)}=(n-1)+(n-2)+S_{(n-2)}=(n-1)+(n-2)+(n-3)+\hdots+1 =\frac{n(n-1)}{2}$$ Luego analizando algunos casos: 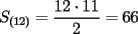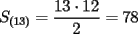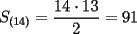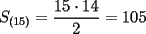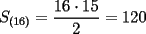$TEX: $\displaystyle S_{(12)}=\frac{12 \cdot 11}{2} = 66$$ $TEX: $\displaystyle S_{(13)}=\frac{13 \cdot 12}{2} = 78$$ $TEX: $\displaystyle S_{(14)}=\frac{14 \cdot 13}{2} = 91$$ $TEX: $\displaystyle S_{(15)}=\frac{15 \cdot 14}{2} = 105$$ $TEX: $\displaystyle S_{(16)}=\frac{16 \cdot 15}{2} = 120$$ Finalmente, a estos resultados se les debe sumar la multiplicacion de la cantidad de niñas por la de niños, puesto que esta es la cantidad de besos entre hombres y mujeres, Finalmente , inspeccionando cual es, nos da que el resultado es que hay 14 niñas y 9 niños, yaque: 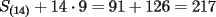$TEX: $\displaystyle S_{(14)}+ 14 \cdot 9=91 + 126 = 217$$ salu2! ^^ --------------------

felipe_contreras... felipe_contreras(IN) Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 8 2006, 08:38 PM Publicado: #4
Maestro Matemático Grupo: Usuario FMAT Mensajes: 90 Registrado: 14-May 05 Desde: 33º30'S 70º40'O Miembro Nº: 18 Nacionalidad: Colegio/Liceo: Sexo:	CITA(Jaime sscc @ Jul 8 2006, 09:57 PM) Esta fecha en 2 palabras : Brute Force No necesariamente, yo lo saqué así Las mujeres saludan con un beso a todo el curso, menos a sí mismas. Los hombre saludas con un beso a todo el curso, menos los hombres. Entonces nos queda: 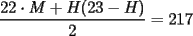$TEX: $\dfrac{22\cdot M+ H(23-H)}{2}=217$$ Con M la cantidad de mujeres y H la cantidad de hombres, y divdiendo por dos para que no se repitan los saludos. También: 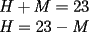$TEX: $H+M=23$<br /><br />$H=23-M$$ Reemplazando: 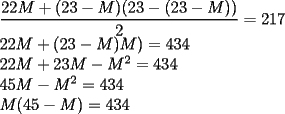$TEX: $\dfrac{22M+ (23-M)(23-(23-M))}{2}=217$<br /><br />$22M+ (23-M)M)=434$<br /><br />$22M+ 23M - M^2=434$<br /><br />$45M - M^2=434$<br /><br />$M(45-M)=434$$ Los divisores naturales de 434 son: 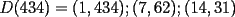$TEX: $D(434)=(1,434);(7,62);(14,31)$$ Los únicos divisores que cumplen la condición son 14 y 31. Por lo tanto son 14 mujeres y 9 hombres. -------------------- "El único primo congruente a uno en módulo cuatro es cinco" A. Gajardo ""I'm going to try to see if I can remember as much to make it sound like I'm smart on the subject."—G. W. Bush, answering a question concerning a possible flu pandemic, Cleveland, July 10, 2007 "I aim to be a competitive nation."—G. W. Bush, San Jose, Calif., April 21, 2006 "Those who enter the country illegally violate the law."— G. W. Bush, Tucson, Ariz., Nov. 28, 2005 "Our enemies are innovative and resourceful, and so are we. They never stop thinking about new ways to harm our country and our people, and neither do we." — G. W. BushWashington, D.C., Aug. 5, 2004

Sasuke7410 Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 8 2006, 10:41 PM Publicado: #5
Principiante Matemático Grupo: Usuario FMAT Mensajes: 8 Registrado: 15-April 06 Miembro Nº: 858	CITA(felipe_contreras(IN) @ Jul 8 2006, 09:38 PM) Los divisores naturales de 434 son: $TEX: $D(434)=(1,434);(7,62);(14,31)$$ Los únicos divisores que cumplen la condición son 14 y 31. Por lo tanto son 14 mujeres y 9 hombres. A q Condicion te refieres???disculpa si la pregunta es tonta pero no entendi

Killua Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 8 2006, 10:45 PM Publicado: #6
Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Sasuke7410 @ Jul 8 2006, 11:41 PM) A q Condicion te refieres???disculpa si la pregunta es tonta pero no entendi Se refiere a las únicas que cumplen 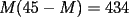$TEX: $M(45-M)=434$$ Saludos PD: más tonto que no dividir por 2 -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy) "A mathematician is a device for turning coffee into theorems" (Paul Erdös)

Killua Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 9 2006, 12:46 PM Publicado: #7
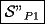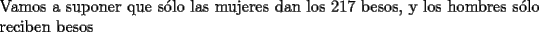Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Antes de ver la final del Mundial , voy a postear una tercera solución del p1 $TEX: $\boxed{\mathcal{S"}_{P1}}$$ $TEX: \noindent Vamos a suponer que s\'olo las mujeres dan los $217$ besos, y los hombres s\'olo reciben besos$ $TEX: \noindent Notemos que, la primera mujer dar\'a $22$ besos a todos sus compa\~neros, la segunda mujer besar\'a a $21$ de sus compa\~neros, excepto a la primera mujer, hasta la \'ultima mujer que s\'olo besar\'a a los hombres (recordemos que se cuentan s\'olo los besos dados y no los recibidos)$ $TEX: \noindent O sea, tenemos que encontrar alg\'un $n$, que es el n\'umero de hombres, tal que:<br /><br />$$22+21+\ldots+n=217$$<br /><br />\noindent Adem\'as, notemos que $217=31\cdot{7}$, y que $22+9=31$, y que adem\'as entre $9$ y $22$ inclusive hay $14$ n\'umeros, lo que nos inspira a usar el principio de Gaussito:<br /><br />$$22+9=31$$<br />$$21+10=31$$<br />$$\ldots$$<br />$$17+14=31$$<br />$$16+15=31$$<br /><br />\noindent En total, $7$ parejas de suma $31$, luego $217=22+21+\ldots+10+9$, por lo tanto el n\'umero de hombres, $n$, es $9$.<br /><br />\noindent Entonces, en el curso hay $9$ hombres y $14$ mujeres$ Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy) "A mathematician is a device for turning coffee into theorems" (Paul Erdös)

FelipeX300 Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 21 2008, 12:04 AM Publicado: #8
Principiante Matemático Grupo: Usuario FMAT Mensajes: 7 Registrado: 10-June 08 Miembro Nº: 26.800 Nacionalidad: Colegio/Liceo: Sexo:	no me pregunten como pero en una de esas tormentosas noches de invierno me quedo dando vuelta el problema en la cabeza pues por reforzamiento de campeonato lo pasaron y no lo pude sacar y una compañera dijo que eran 10 mujeres parece pero considero que el numero de besos entre mujeres era mujeres por mujeres lo que esta mal pues las muejres no se saludan con si mismas aunq hay algunas bien.... no es el caso bien no recuerdo como pero para calcular los besos de muejeres era como $TEX: \[<br />\frac{{x^2 }}<br />{2} - \frac{x}<br />{2}<br />\]<br />$ y eso asi bien simplificado porq recuerdo haberlo simplificado mucho bien es inutil postear esto porq no tiene un trasfonde pero la formula da aunq mi cabeza no archivo el procedimiento exacto XD bueno eso seria aporte inutil mi especialidad XD

« Posterior · Cuarta Fecha · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 6th March 2025 - 09:27 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.