2ª grado - Foro fmat.cl

Reglamento Sector Propuestos

Para un correcto uso de este foro debes leer estas reglas:

Los creadores de los temas deben ceñirse a los contenidos PSU.
Las respuestas deben ir con un desarrollo que explique el resultado final.
Se prohiben las peleas, descalificaciones y desvirtuar el tema original.
El creador del tema puede "upear" su tema, después de 5 dias de que lo haya posteado.
- No se permite hacer mas de 3 "up" por tema.
El titulo del tema debe ser representativo al problema que se posteara.
- Ejemplo: "Ejercicio de Circunferencias, Potencias, Racionalización, etc..."
Después de que el autor del tema haya quedado satisfecho con las respuestas, debera escribir "resuelto" en el título del tema o en la descripción de la discusión.

Staff FMAT

2ª grado, quero saber si la pauta esta buena

pablomarcelo Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 20 2008, 01:46 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 920 Registrado: 14-October 08 Miembro Nº: 36.137 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	QUESTION.PNG ( 11.92k ) Número de descargas: 0 $TEX: <br /><br />\[<br />\begin{gathered}<br /> a){\text{ }}\left( {0, - 10} \right) \hfill \\<br /> b){\text{ }}\left( {3, - 10} \right) \hfill \\<br /> c){\text{ }}\left( { - 2,5} \right) \hfill \\<br /> d){\text{ }}\left( { - 10,0} \right) \hfill \\<br /> e){\text{ falta informacion para determinarlo}} \hfill \\ <br />\end{gathered} <br />\]<br /><br /><br />$ pd: se me olvido poner el x y el y en la imagen linea vertical eje y

Ussop Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 20 2008, 02:03 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.349 Registrado: 8-October 07 Desde: Quilicura Miembro Nº: 11.057 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \[<br />\begin{gathered}<br /> x_1 = - 2 \hfill \\<br /> x_2 = 5 \hfill \\<br /> f\left( x \right) = ax + bx + c \hfill \\<br /> \frac{c}<br />{a} = x_1 \cdot x_2 = - 10 \hfill \\<br /> \frac{{ - b}}<br />{a} = 3 \hfill \\<br /> x^2 - 3x - 10 = 0 \hfill \\<br /> c = 10 \hfill \\<br /> \boxed{A = \left( {0, - 10} \right)} \hfill \\ <br />\end{gathered} <br />\]<br />$ Mensaje modificado por max_734 el Oct 20 2008, 02:13 PM -------------------- Plan Comun Ingenieria USM 2009 Santiago Ingenieria Civil Electrica Usm 2010 Santiago

pablomarcelo Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 20 2008, 03:36 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 920 Registrado: 14-October 08 Miembro Nº: 36.137 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: <br /><br />\[<br />\begin{gathered}<br /> {\text{parece que tu dividiste}} \hfill \\<br /> ax^2 + bx + c \hfill \\<br /> ax^2 + bx + c/:a \hfill \\<br /> x^2 + \frac{b}<br />{a}x + \frac{c}<br />{a} \hfill \\<br /> x^2 - 3x - 10 \hfill \\<br /> \hfill \\<br /> {\text{pero al dividir una ecuacion de 2 grado sus raices quedan }} \hfill \\<br /> {\text{iguales }}{\text{,en cambio su maximo o minimo cambia}} \hfill \\<br /> demostracion \hfill \\<br /> ax^2 + bx + c \hfill \\<br /> \min \max = \frac{{4ac - b^2 }}<br />{{4a}} \hfill \\<br /> \hfill \\<br /> ax^2 + bx + c/ \times n \hfill \\<br /> nax^2 + nbx + nc \hfill \\<br /> \min \max = \frac{{4n^2 ac - n^2 b^2 }}<br />{{4na}} = \frac{{n(4ac - b^2 )}}<br />{{4a}} \hfill \\<br /> \hfill \\<br /> .....{\text{tambien su interseccion al eje y}} \hfill \\<br /> {\text{asi que }}ax^2 + bx + c{\text{ y }}x^2 + \frac{b}<br />{a}x + \frac{c}<br />{a} \hfill \\<br /> {\text{no tienen la misma grafica}} \hfill \\<br /> \hfill \\<br /> {\text{pero la pauta dice A pero a mi no me convence}} \hfill \\ <br />\end{gathered} <br />\]<br /><br />ayuda please <br />esta pregunta me esta carcomiendo por dentro<br /><br /><br /><br />$

snw Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 20 2008, 03:45 PM Publicado: #4
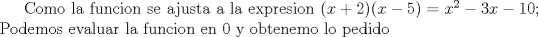
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: Como la funcion se ajusta a la expresion $(x+2)(x-5)=x^2-3x-10$; Podemos evaluar la funcion en 0 y obtenemo lo pedido$ -------------------- blep

CyedqD Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 20 2008, 03:45 PM Publicado: #5
Coordinador General Gran Maraton PSU Final 2008 Grupo: Moderador Mensajes: 1.607 Registrado: 11-June 07 Desde: Peñalolen, Stgo Miembro Nº: 6.641 Nacionalidad: Universidad: Sexo:	Momento, en esta parte cometiste un error: CITA(max_734 @ Oct 20 2008, 03:03 PM) $TEX: \[<br />\begin{gathered}<br /> f\left( x \right) = ax + bx + c \hfill \\<br /> x^2 - 3x - 10 = 0 \hfill \\<br />\end{gathered} <br />\]<br />$ Como es que pasas de tener una funcion a tener una ecuacion? Recordar que una ecuacion no es lo mismo que una funcion, pues solo la funcion determina una grafica. Tipicamente una funcion de segundo grado es de la siguiente forma: $TEX: \[<br />f_{\left( x \right)} = ax^2 + bx + c<br />\]<br />$ Si tenemos que sus raices son $TEX: \[x_1 ,x_2 \]$ la podemos factorizar de este modo: $TEX: <br />\[<br />f_{\left( x \right)} = a\left( {x - x_1 } \right)\left( {x - x_2 } \right)<br />\]<br />$ Ahora observa que "a" es independiente de las raices de la funcion. O sea el tener esos dos puntos, no te permite determinar la grafica de esa parabola. Puedes tener: $TEX: \[<br />f_{\left( x \right)} = \left( {x + 2} \right)\left( {x - 5} \right) = x^2 - 3x - 10<br />\]$ o $TEX: \[<br />f_{\left( x \right)} = 2\left( {x + 2} \right)\left( {x - 5} \right) = 2x^2 - 6x - 20<br />\]$ y las raices seran las mismas, mientras que el corte con el eje y varia. Por tanto la respuesta correcta en realidad es E. 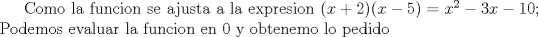CITA(snw @ Oct 20 2008, 04:45 PM) $TEX: Como la funcion se ajusta a la expresion $(x+2)(x-5)=x^2-3x-10$; Podemos evaluar la funcion en 0 y obtenemo lo pedido$ La funcion tambien se podria ajustar a la expresion $TEX: \[<br />f_{\left( x \right)} = 1000\left( {x + 2} \right)\left( {x - 5} \right)<br />\]<br />$ que da un valor distinto al evaluarla en cero. --------------------

snw Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 20 2008, 03:49 PM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(CyedqD @ Oct 20 2008, 05:45 PM) Momento, en esta parte cometiste un error: Como es que pasas de tener una funcion a tener una ecuacion? Recordar que una ecuacion no es lo mismo que una funcion, pues solo la funcion determina una grafica. Tipicamente una funcion de segundo grado es de la siguiente forma: $TEX: \[<br />f_{\left( x \right)} = ax^2 + bx + c<br />\]<br />$ Si tenemos que sus raices son $TEX: \[x_1 ,x_2 \]$ la podemos factorizar de este modo: $TEX: <br />\[<br />f_{\left( x \right)} = a\left( {x - x_1 } \right)\left( {x - x_2 } \right)<br />\]<br />$ Ahora observa que "a" es independiente de las raices de la funcion. O sea el tener esos dos puntos, no te permite determinar la grafica de esa parabola. Puedes tener: $TEX: \[<br />f_{\left( x \right)} = \left( {x + 2} \right)\left( {x - 5} \right) = x^2 - 3x - 10<br />\]$ o $TEX: \[<br />f_{\left( x \right)} = 2\left( {x + 2} \right)\left( {x - 5} \right) = 2x^2 - 6x - 20<br />\]$ y las raices seran las mismas, mientras que el corte con el eje y varia. Por tanto la respuesta correcta en realidad es E. La funcion tambien se podria ajustar a la expresion $TEX: \[<br />f_{\left( x \right)} = 1000\left( {x + 2} \right)\left( {x - 5} \right)<br />\]<br />$ que da un valor distinto al evaluarla en cero. omg tienes razon -------------------- blep

s3b4s Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 20 2008, 04:58 PM Publicado: #7
Dios Matemático Grupo: Usuario FMAT Mensajes: 307 Registrado: 29-March 08 Desde: Valpo/Stgo Miembro Nº: 18.394 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	que malos los distractores xD de donde es este ejercicio? -------------------- Last.fm 1. Mathematics is the language of Nature. 2. Everything around us can be represented and understood through numbers. 3. If you graph the numbers of any system, patterns emerge. Therefore: There are patterns everywhere in nature.

« Posterior · Problemas Propuestos · Anterior »

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):