|
|
|
|
|
|
|
  |
 Oct 18 2008, 06:44 PM Oct 18 2008, 06:44 PM
Publicado:
#1
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Sexta Fecha - 18 de Octubre de 2008 (Primera Recuperativa)
1. Rosita tiene veinte monedas. Unas son de $10, otras son de $20 y otras de $50, por un valor total de $500. Si tiene más monedas de $50 que de $10. ¿Cuántas monedas tiene de cada tipo? Aclaración: Rosita tiene al menos una moneda de cada tipo. 2. En un triángulo 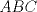 se verifica que se verifica que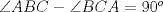 . Muestre que la altura desde . Muestre que la altura desde 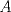 es tangente a la circunferencia circunscrita al triángulo es tangente a la circunferencia circunscrita al triángulo 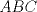 . .Saludos. Mensaje modificado por Rurouni Kenshin el Oct 18 2008, 09:11 PM
Razón de edición: Un leve agregado :)
Archivo(s) Adjunto(s)
-------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Oct 19 2008, 01:41 PM Oct 19 2008, 01:41 PM
Publicado:
#2
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 766 Registrado: 6-May 07 Desde: San Pedro de la Paz, Concepción Miembro Nº: 5.639 Nacionalidad:  Colegio/Liceo:  Sexo:  |
P2
salu2 -------------------- asdf
|
|
|
|
 Nov 2 2008, 02:02 PM Nov 2 2008, 02:02 PM
Publicado:
#3
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 26 Registrado: 1-November 08 Desde: Santiago de Chile Miembro Nº: 37.535 Nacionalidad:  Colegio/Liceo:  Sexo:  |
1. Rosita tiene veinte monedas. Unas son de $10, otras son de $20 y otras de $50, por un valor total de $500. Si tiene más monedas de $50 que de $10. ¿Cuántas monedas tiene de cada tipo? Aclaración: Rosita tiene al menos una moneda de cada tipo. Sean 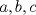 las cantidades de monedas de las cantidades de monedas de 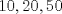 respectivamente. respectivamente.Tal que tenemos las siguiente condiciones 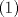 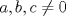 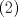 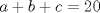 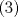  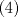 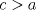 Dividiendo por 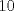 en la igualdad en en la igualdad en 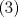 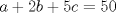 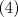 Amplificando por 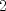 en en 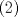 se tiene se tiene 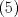 Luego 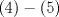 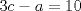 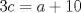 Sabemos que 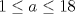 Por ende los valores que puede tomar  son son 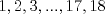 De estos valores se descartan inmediatamente 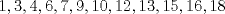 ya que ya que  no sería divisible por no sería divisible por  Tenemos los siguiente casos: 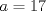 implica que implica que 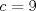 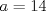 implica que implica que 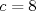 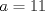 implica que implica que 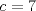 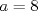 implica que implica que 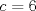 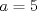 implica que implica que 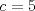 Todos estos casos se descartan pues contradicen que 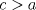 Por ende el único caso válido es 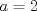 , esto implica que , esto implica que 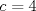 , luego concluimos que por condición , luego concluimos que por condición 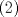 que que  . Vemos que los valores de . Vemos que los valores de 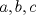 cumplen todas las condiciones pedidas. cumplen todas las condiciones pedidas.Finalmente hay 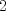 monedas de monedas de 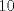 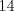 monedas de monedas de 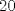  monedas de monedas de 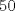
-------------------- Aquiles Esquivel Medrazo
Estudiante Cursando 7º Básico |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 02:54 PM |












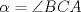 y
y 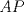 la altura trazada desde A. Por enunciado tenemos
la altura trazada desde A. Por enunciado tenemos 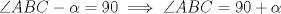 . Trazamos
. Trazamos 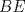 tal que
tal que 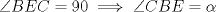 . Prolongamos
. Prolongamos 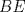 hasta que se intersecte con la circunferencia en un punto D, y trazamos
hasta que se intersecte con la circunferencia en un punto D, y trazamos 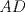 . Notar que
. Notar que 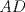 es diametro, ya que
es diametro, ya que 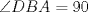 , por lo que el problema se reduce a demostrar que
, por lo que el problema se reduce a demostrar que 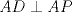 .
.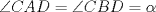 .
.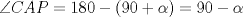 .
.