|
|
|
|
|
|
|
  |
 Oct 3 2008, 10:51 PM Oct 3 2008, 10:51 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Colaborador Platinum Mensajes: 1.067 Registrado: 11-September 07 Desde: Coquimbo Miembro Nº: 10.097 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Una partícula se lanza desde la superficie
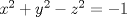 desde el punto desde el punto 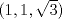 a lo largo de la dirección normal a dicha superficie, dirigida hacia el plano XY, en un instante de tiempo t=0 y con una rapidez de 10 unidades por segundo. a lo largo de la dirección normal a dicha superficie, dirigida hacia el plano XY, en un instante de tiempo t=0 y con una rapidez de 10 unidades por segundo.¿Cuándo y dónde dicha partícula cruza el plano XY? Saludos. --------------------  "¿Qué es la vida? Una ilusión, una sombra, una ficción, y el mayor bien es pequeño: que toda la vida es sueño, y los sueños, sueños son." |
|
|
|
 Oct 3 2013, 10:17 PM Oct 3 2013, 10:17 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 947 Registrado: 28-September 07 Desde: Santiago Miembro Nº: 10.639 Nacionalidad:  Universidad:  Sexo:  |
![TEX: <br />La superficie dada es el hiperboloide de 2 hojas<br />\[F(x,y,z) = x^2+y^2-z^2+1=0\]<br />La dirección normal a la superficie está dada por su gradiente:<br />\[ \nabla F(x,y,z) = (2x,2y,-2z) \]<br />La dirección normal a la superficie en el punto $(1,1,\sqrt{3})$ (que porsupuesto corresponde a la hoja superior del hiperboloide) es<br />\[ \nabla F(1,1,\sqrt{3}) = (2,2,-2\sqrt{3}) \]<br />Esta dirección tiene tercera coordenada negativa, por lo que su vector está apuntando en dirección al plano $XY$.<br />La partícula sigue una trayectoria lineal, en dirección $(2,2,-2\sqrt{3})$, partiendo en $t=0$ en el punto $(1,1,\sqrt{3})$. La dirección del primer vector también representa la velocidad de la partícula. La rapidez de este vector es $\|(2,2,-2\sqrt{3})\| = 2\sqrt{5}$. Luego, el vector velocidad que tiene la misma dirección que $(2,2,-2\sqrt{3})$ pero con rapidez $10$ es el vector $\displaystyle \frac{10}{2\sqrt{5}}(2,2,-2\sqrt{3}) = (2\sqrt{5},2\sqrt{5},-2\sqrt{15})$. Así, la ecuación vectorial de dicha recta está dada por<br />\[ (x,y,z) = (1,1,\sqrt{3}) + t \cdot (2\sqrt{5},2\sqrt{5},-2\sqrt{15}) \hspace{1cm} \forall t\geq 0 \]<br />cuya ecuación paramétrica está dada por las coordenadas<br />\begin{align*}<br /> x(t) &= 1+2\sqrt{5}t \\<br /> y(t) &= 1+2\sqrt{5}t \\<br /> z(t) &= \sqrt{3} -2\sqrt{15}t<br />\end{align*}<br />La partícula llega al plano $XY$ cuando $\displaystyle z(t^{*})=0 \Leftrightarrow t^{*} = \frac{\sqrt{5}}{10}$. El lugar donde esto sucede es en<br />\[ (x^{*},y^{*},z^{*}) = (1,1,\sqrt{3}) + \frac{\sqrt{5}}{10} \cdot (2\sqrt{5},2\sqrt{5},-2\sqrt{15}) = \left(2,2,0\right) \]<br />](/tex-image/855ef0ed9094ec1d298e4547ccd22157.png)
Mensaje modificado por Laðeralus el Oct 4 2013, 03:16 AM |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 04:59 AM |








