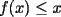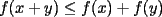|
|
|
|
|
|
|
  |
 Jul 7 2005, 12:14 AM Jul 7 2005, 12:14 AM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 558 Registrado: 14-May 05 Desde: Maipú, Stgo, Chile Miembro Nº: 27 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
y aki va el 1° problema de la tanda........igual no tan dificil pa comenzar
Propuesto 1 Demuestre que si 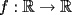 cumple las desigualdades ( cumple las desigualdades (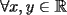 ): ):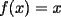 , para todo , para todo 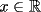 Fuente: Olimpiada Nacional 1990 (modificado) -------------------- El peor defecto del ignorante es que ignora su propia ignorancia................
|
|
|
|
 Jul 7 2005, 12:33 AM Jul 7 2005, 12:33 AM
Publicado:
#2
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Mi propuesto es:
Propuesto 2 En la figura 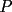 y y 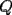 son los centros de dos circunferencias. son los centros de dos circunferencias.Ademas se tiene que 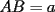 y y 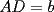 . Calcular el valor de . Calcular el valor de 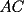 en funcion de en funcion de  y y 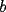 . . screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img248.imageshack.us/img248/9168/propuesto13nd.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img248.imageshack.us/img248/9168/propuesto13nd.png');}" />Como veran no me tire muy dificil,sin embargo es un desafio que no pueden dejar de hacer...saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jul 7 2005, 01:25 AM Jul 7 2005, 01:25 AM
Publicado:
#3
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 8 Registrado: 13-May 05 Desde: Beauchef 850 Miembro Nº: 13 |
Notemos que sólo basta demostrar que
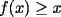 ya que al unir esto con (i) encontraremos lo pedido. ya que al unir esto con (i) encontraremos lo pedido.calculemos primero 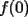 ... por (ii): ... por (ii):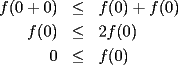 pero por (i): 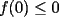 . Luego . Luego 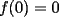 . Ahora usemos (ii) para concluir: . Ahora usemos (ii) para concluir: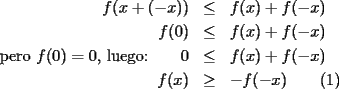 usando apropiadamente (i) con 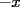 en lugar de en lugar de  : :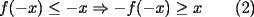 de donte por transitividad del 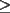 en (1) y (2) se deduce finalmente que en (1) y (2) se deduce finalmente que 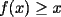 , y como , y como 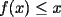 , luego , luego 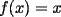 espero que mi solución sea correcta saludos -------------------- si quieres tener mucho $$ presiona shift+4 varias veces
|
|
|
|
 Jul 7 2005, 11:29 AM Jul 7 2005, 11:29 AM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Aquí les regalo el tercer problema de la semana... para los + pequeños de la casa (también se lo propongo a la Antonia... el que entienda, bien
Problema 3: Calcule todos los 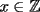 que cumplen con el siguiente sistema de congruencias: que cumplen con el siguiente sistema de congruencias: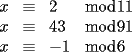 El problema no es tan atractivo pero da para algo de discusión sobre el tema... ojalá podamos discutirlo un poco... Les recuerdo que, por ser un sistema de congruencias, la incógnita  debe satisfacerlas todas, simultáneamente debe satisfacerlas todas, simultáneamenteQue estén muy bien -------------------- |
|
|
|
 Jul 7 2005, 01:12 PM Jul 7 2005, 01:12 PM
Publicado:
#5
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 414 Registrado: 19-May 05 Desde: puente alto, santiago Miembro Nº: 45 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
aqui va el cuarto de la secuencia:
Propuesto 4 Hallar los cuadrados perfectos de 6 cifras tales que si se les descompone en grupos de dos cifras, el número formado por las dos centrales es igual a la suma de los números formados por los otros dos pares. ese es el problema, aclaro bien el enunciado por cualquier duda, por ejemplo el numero 235734 es un numero que cumple con la segunda propiedad ya que 23+34=57, pero no es un numero de los que estamos buscando, ya que 235734 no es cuadrado perfecto. Espero que les guste y lo resuelvan Sin otro particular se despide Francisco Muñoz Espinoza -------------------- "No tenemos la solucion a todos los problemas del mundo en nuestras manos... Pero frente a los problemas del mundo tenemos nuestras manos..."
Teresa de Calcuta |
|
|
|
 Jul 7 2005, 03:54 PM Jul 7 2005, 03:54 PM
Publicado:
#6
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 11 Registrado: 6-July 05 Miembro Nº: 135 |
PAL PROBLEMA 3 CREO
la primera  es de la forma es de la forma 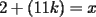 donde donde 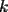 es un numero entero cualquiera es un numero entero cualquierala segunda es 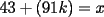 donde donde 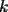 es un numero entero cualquiera es un numero entero cualquierala tercera es 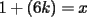 donde donde 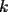 es un numero entero cualquiera es un numero entero cualquiera
-------------------- si alguien me kiere enseñar q me enseñe, si puede...
|
|
|
|
 Jul 7 2005, 05:04 PM Jul 7 2005, 05:04 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Recuerdo que debe ser la misma
 que cumpla todas las congruencias al mismo tiempo... por algo dije que es un sistema de congruencias... las soluciones deben ser números enteros, así que no tengan reparos en usar números positivos, negativos o el 0 que cumpla todas las congruencias al mismo tiempo... por algo dije que es un sistema de congruencias... las soluciones deben ser números enteros, así que no tengan reparos en usar números positivos, negativos o el 0 Me gustó la idea de colocar las cosas en términos de letras 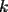 , pero debes hacerlo con un poco más de cuidado... si usas la misma letra , pero debes hacerlo con un poco más de cuidado... si usas la misma letra 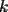 para todo, te vas a confundir... ahí tienen muchas pistas... para todo, te vas a confundir... ahí tienen muchas pistas...Voy a esperar una solución para comentar un poco más al respecto Preferiría que esos mensajes que escribiste, queden, porque ayudan a aclarar algunas cosas, algunos errores que podrían cometer al atacar el problema (y la idea es que se equivoquen aquí, para que podamos corregir esos detalles a tiempo, en vez de equivocarse en el campeonato escolar o en las olimpiadas de matemáticas, o en la PSU...) Recuerda que de los errores se aprende, a veces de los propios, otras veces de los errores que cometen los demás... no hay que sentir vergüenza de equivocarse, porque nadie es perfecto... la idea es reconocerlo -------------------- |
|
|
|
| Believer |
 Jul 7 2005, 08:32 PM Jul 7 2005, 08:32 PM
Publicado:
#8
|
|
Invitado |
CITA(xsebastian) Problema 3: Calcule todos los 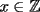 que cumplen con el siguiente sistema de congruencias: que cumplen con el siguiente sistema de congruencias: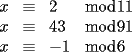 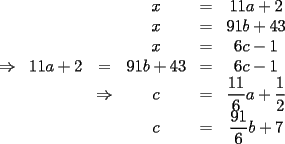 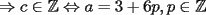 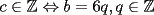 Luego, 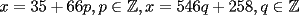 , son todas las soluciones enteras del sistema. , son todas las soluciones enteras del sistema.Creo. |
|
|
|
 Jul 7 2005, 10:27 PM Jul 7 2005, 10:27 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Este intento está + cerca de la solución... tienes que ver cosas de divisibilidad... pero cometiste un error de signo... vas por buen camino, arregla ese detalle y corrige tu solución
No está correcto, pero va cerca -------------------- |
|
|
|
 Jul 7 2005, 10:57 PM Jul 7 2005, 10:57 PM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 558 Registrado: 14-May 05 Desde: Maipú, Stgo, Chile Miembro Nº: 27 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
gonzalo, tu respuesta esta impecable, nada k agregar.
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 25th April 2025 - 11:49 PM |