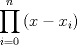|
|
|
|
|
|
|
  |
 Sep 17 2009, 12:22 AM Sep 17 2009, 12:22 AM
Publicado:
#91
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.413 Registrado: 13-March 08 Desde: Al frente del mundo Magico Miembro Nº: 16.846 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
bueno suponiendo que lo son xD y abusando de la notacion D=
![TEX: \[\begin{gathered}<br /> y = \prod\limits_{i = 0}^n {\left( {x - {x_i}} \right)} = \left( {x - {x_0}} \right)\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)...\left( {x - {x_n}} \right) \hfill \\<br /> \ln \left( y \right) = \ln \left[ {\left( {x - {x_0}} \right)\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)...\left( {x - {x_n}} \right)} \right] \hfill \\<br /> \ln \left( y \right) = \ln \left( {x - {x_0}} \right) + \ln \left( {x - {x_1}} \right) + \ln \left( {x - {x_2}} \right) + ... + \ln \left( {x - {x_n}} \right) \hfill \\<br /> {\left( {\ln \left( y \right)} \right)^\prime } = {\left[ {\ln \left( {x - {x_0}} \right) + \ln \left( {x - {x_1}} \right) + \ln \left( {x - {x_2}} \right) + ... + \ln \left( {x - {x_n}} \right)} \right]^\prime } \hfill \\<br /> \frac{{y'}}<br />{y} = \frac{1}<br />{{x - {x_0}}} + \frac{1}<br />{{x - {x_1}}} + \frac{1}<br />{{x - {x_2}}} + ... + \frac{1}<br />{{x - {x_n}}} \hfill \\<br /> y' = \prod\limits_{i = 0}^n {\left( {x - {x_i}} \right)} \cdot \left( {\frac{1}<br />{{x - {x_0}}} + \frac{1}<br />{{x - {x_1}}} + \frac{1}<br />{{x - {x_2}}} + ... + \frac{1}<br />{{x - {x_n}}}} \right) \hfill \\ <br />\end{gathered} \]<br />](./tex/271614572f954efc7fad8add09dd9b65.png)
Mensaje modificado por danielomalmsteen el Sep 17 2009, 12:22 AM --------------------  |
|
|
|
 Sep 17 2009, 12:23 AM Sep 17 2009, 12:23 AM
Publicado:
#92
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.756 Registrado: 16-September 07 Desde: al frente del Express Miembro Nº: 10.238 Nacionalidad:  Universidad:  Sexo:  |
Gueno... acá te las traigo, piter... Hola... vengo a flotar... HINT!! Acordarse de la definición de la derivada de un producto de dos funciones... ahora extrapólenla a n funciones... les quedará algo así... 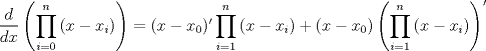 ... ...Bueno... chaaaaaooooooooooo ahaa esta muerto esto po cabros,pa qe revivirlo xDDDD ...yo cacho qe el loco qeria en su tiempo qe aplicaran un sexi logaritmo --------------------  Ahora van quedando en el foro solo los niñitos tontitos graves, que lata... u.u  |
|
|
|
 Sep 19 2009, 05:15 PM Sep 19 2009, 05:15 PM
Publicado:
#93
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 34 Registrado: 12-May 08 Desde: Valdivia, Región de los Ríos. Miembro Nº: 22.858 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Después de casi un año de haber posteado esa cosa, ya se me había olvidado cómo resolverla...
En fin... Volviendo al problema en sí, siguiendo lo que hizo el Está bien, porque si se hace como yo propuse hace casi un año atrás ( Propone tu problema, danielomalmsteen, para que los foreros tengan pega que hacer... jajajajaja Saludos!!  zippy.pdf ( 35.41k )
Número de descargas: 49
zippy.pdf ( 35.41k )
Número de descargas: 49Mensaje modificado por Alexei Zaitsev el Sep 19 2009, 05:19 PM -------------------- Marco Antonio Gaete. Estudiante Ingeniería Civil Acústica. Promoción 2006. Universidad Austral de Chile. |
|
|
|
 Sep 19 2009, 05:45 PM Sep 19 2009, 05:45 PM
Publicado:
#94
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.413 Registrado: 13-March 08 Desde: Al frente del mundo Magico Miembro Nº: 16.846 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
xDDDD
aqui va xd ![TEX: \[\begin{gathered}<br /> {\text{Dada }}f\left( x \right) = \sum\limits_{i = 1}^n {{{\left( {{\alpha _i} - x} \right)}^2}} \hfill \\<br /> {\text{Encuentre su minimo con }}{\alpha _i} \in \mathbb{R}{\text{ y }}i = 1...n{\text{ y demustre que}} \hfill \\<br /> {\left( {\sum\limits_{i = 1}^n {{\alpha _i}} } \right)^2} \leqslant n\sum\limits_{i = 1}^n {\alpha _i^2} \hfill \\ <br />\end{gathered} \]<br />](./tex/92954e27be6f178ffe27b5f5cbeebc9f.png)
--------------------  |
|
|
|
 Jul 21 2011, 11:31 PM Jul 21 2011, 11:31 PM
Publicado:
#95
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 858 Registrado: 20-August 09 Desde: In my House Miembro Nº: 57.323 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
xDDDD aqui va xd ![TEX: \[\begin{gathered}<br /> {\text{Dada }}f\left( x \right) = \sum\limits_{i = 1}^n {{{\left( {{\alpha _i} - x} \right)}^2}} \hfill \\<br /> {\text{Encuentre su minimo con }}{\alpha _i} \in \mathbb{R}{\text{ y }}i = 1...n{\text{ y demustre que}} \hfill \\<br /> {\left( {\sum\limits_{i = 1}^n {{\alpha _i}} } \right)^2} \leqslant n\sum\limits_{i = 1}^n {\alpha _i^2} \hfill \\ <br />\end{gathered} \]<br />](./tex/92954e27be6f178ffe27b5f5cbeebc9f.png) 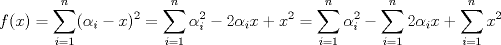 Luego 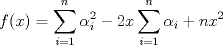 Como 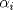 no depende de no depende de  , luego sea , luego sea 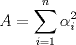 y y 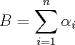 , por lo tanto tenemos que , por lo tanto tenemos que 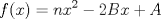 , por lo tanto la derivada de , por lo tanto la derivada de 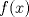 es es 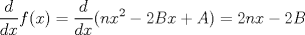 Podemos ver fácilmente que 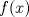 representa una parábola convexa por el hecho de que representa una parábola convexa por el hecho de que 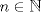 , luego su mínimo se encuentra en su vértice, por lo tanto , luego su mínimo se encuentra en su vértice, por lo tanto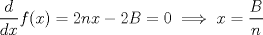 , finalmente , finalmente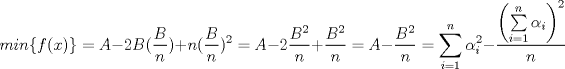 Por la desigualdad de cauchy - schwarz tenemos que 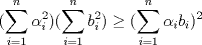 Basta con tomar 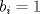 y obtenemos y obtenemos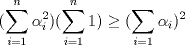 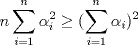
Mensaje modificado por EnemyOfGod286 el Jul 21 2011, 11:36 PM |
|
|
|
 Jul 23 2011, 10:04 PM Jul 23 2011, 10:04 PM
Publicado:
#96
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 858 Registrado: 20-August 09 Desde: In my House Miembro Nº: 57.323 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
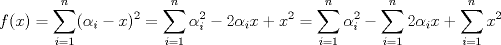 Luego 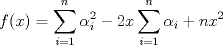 Como 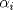 no depende de no depende de  , luego sea , luego sea 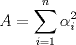 y y 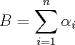 , por lo tanto tenemos que , por lo tanto tenemos que 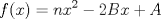 , por lo tanto la derivada de , por lo tanto la derivada de 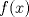 es es 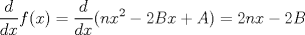 Podemos ver fácilmente que 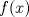 representa una parábola convexa por el hecho de que representa una parábola convexa por el hecho de que 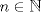 , luego su mínimo se encuentra en su vértice, por lo tanto , luego su mínimo se encuentra en su vértice, por lo tanto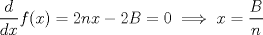 , finalmente , finalmente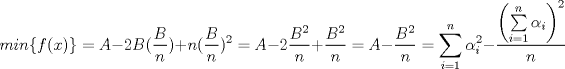 Por la desigualdad de cauchy - schwarz tenemos que 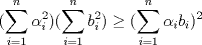 Basta con tomar 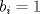 y obtenemos y obtenemos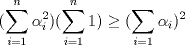 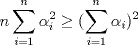 Otra forma de ver la desigualdad (y se me ocurrio recién ahora xD) es lo siguiente Podemos ver fácilmente que 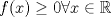 , por lo tanto podemos concluir que , por lo tanto podemos concluir que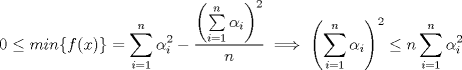 |
|
|
|
 Jul 27 2011, 11:52 AM Jul 27 2011, 11:52 AM
Publicado:
#97
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.847 Registrado: 3-October 09 Miembro Nº: 59.760 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
|
|
|
|
 Sep 8 2011, 02:39 PM Sep 8 2011, 02:39 PM
Publicado:
#98
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 128 Registrado: 18-March 08 Desde: Valdivia y varias partes que sinceramente no te debería importar XD Miembro Nº: 17.202 Nacionalidad:  Universidad:  Sexo:  |
Cuando quieran propongan el ejercicio xD
-------------------- Estudiante de Ingeniería Civil Acústica Universidad Austral de Chile  CITA “Las matemáticas son la música de la razón” James Joseph Silvestre (1814-1897). Matemático británico. “El álgebra es generosa: a menudo da más de lo que se le pide” D’Alembert (1717-1783). Matemático y filósofo francés. “La música es la aritmética de los sonidos, como la óptica es la geometría de la luz.” Claude Debussy (1862-1918) Compositor Francés “La música es un ejercicio aritmético ocultado del alma, que no sabe que está contando.” “La música es el placer que experimenta la mente humana al contar sin darse cuenta de que está contando.” Gottfried Wilhelm Leibniz(1646-1716). Filósofo y Matemático alemán.  Un país que no investiga es un país que no progresa MySpace de Azotth MySpace de Denun |
|
|
|
 Nov 6 2011, 09:34 AM Nov 6 2011, 09:34 AM
Publicado:
#99
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.847 Registrado: 3-October 09 Miembro Nº: 59.760 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
|
|
|
|
 Mar 19 2012, 10:27 AM Mar 19 2012, 10:27 AM
Publicado:
#100
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 128 Registrado: 18-March 08 Desde: Valdivia y varias partes que sinceramente no te debería importar XD Miembro Nº: 17.202 Nacionalidad:  Universidad:  Sexo:  |
-------------------- Estudiante de Ingeniería Civil Acústica Universidad Austral de Chile  CITA “Las matemáticas son la música de la razón” James Joseph Silvestre (1814-1897). Matemático británico. “El álgebra es generosa: a menudo da más de lo que se le pide” D’Alembert (1717-1783). Matemático y filósofo francés. “La música es la aritmética de los sonidos, como la óptica es la geometría de la luz.” Claude Debussy (1862-1918) Compositor Francés “La música es un ejercicio aritmético ocultado del alma, que no sabe que está contando.” “La música es el placer que experimenta la mente humana al contar sin darse cuenta de que está contando.” Gottfried Wilhelm Leibniz(1646-1716). Filósofo y Matemático alemán.  Un país que no investiga es un país que no progresa MySpace de Azotth MySpace de Denun |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 02:54 PM |