Derivatón Uach - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Austral de Chile > Cálculo I

10 Páginas:

< 1 2 3 4 5 > »

Reply to this topic

Start new topic

Derivatón Uach, versión de prueba

JoNy_SaTiE Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 2 2008, 12:11 PM Publicado: #21
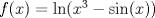Dios Matemático Supremo Grupo: Colaborador Gold Mensajes: 1.118 Registrado: 11-September 05 Desde: Valdivia/Ancud Miembro Nº: 302 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	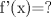CITA(Ivan20i @ Sep 28 2008, 08:51 PM) $TEX: $f(x)=\ln (x^3 - \sin(x) )$$ $TEX: f'(x)=?$ Para que no muera la Derivatón: En este problema hay que aplicar la regla de la cadena. 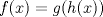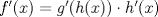Cada vez que tenemos una función compuesta, $TEX: $f(x)=g(h(x))$$ se cumple que $TEX: $f'(x)=g'(h(x)) \cdot h'(x)$$ Entonces, aquí tenemos 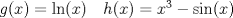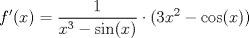$TEX: $g(x)=\ln (x) \quad h(x)=x^3-\sin (x)$$ $TEX: $$ f'(x)=\dfrac{1}{x^3-\sin (x)}\cdot (3x^2-\cos(x))$$$ -------------------- Comienza a crear documentos con LaTeX. Ya usas LaTeX y quieres aprender un poco más ... pincha aquí Si eres de la UaCH ... únete a la causa !!! J. Jonathan H. Oberreuter A. Universidad Austral de Chile - RWTH Aachen alumni Est. Magister en Acústica y Vibraciones Ingeniero Civil Acústico (E) Bachiller y Licenciado en Cs. de la Ingeniería

Pedro² Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 8 2008, 02:37 PM Publicado: #22
Dios Matemático Supremo Grupo: Colaborador Platinum Mensajes: 824 Registrado: 15-October 07 Desde: Valparaíso Miembro Nº: 11.342 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Demuestre, mediante la definición de derivada que 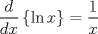$TEX: $\dfrac{d}{dx}\left\{\ln{x}\right\} = \dfrac{1}{x}$$ Saludos -------------------- Pedro P. Montero Silva Estudiante de Licenciatura en Ciencias, Mención Matemática* - Mechón 2009* "One rather curious conclusion emerges, that pure mathematics is on the whole distinctly more useful than applied. A pure mathematician seems to have the advantage on the practical as well as on the aesthetic side. For what is useful above all is technique, and mathematical technique is taught mainly through pure mathematics." G.H. Hardy

Nicte Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 11 2008, 11:24 PM Publicado: #23
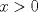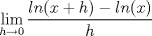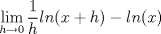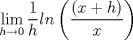Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 28 Registrado: 14-April 08 Desde: Valdivia Miembro Nº: 20.061 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	para 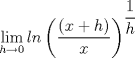$TEX: $x>0$$ $TEX: $\displaystyle \lim_{h\rightarrow 0}\displaystyle \frac{ln(x+h)-ln(x)}{h}$$ $TEX: $\displaystyle \lim_{h\rightarrow 0}\displaystyle \frac{1}{h}ln(x+h)-ln(x)$$ $TEX: $\displaystyle \lim_{h\rightarrow 0}\displaystyle \frac{1}{h}ln\left( \displaystyle \frac{(x+h)}{x}\right)$$ $TEX: $\displaystyle \lim_{h\rightarrow 0}ln \left(\displaystyle \frac{(x+h)}{x}\right)^{\displaystyle \frac{1}{h}}$$ $TEX: $Ln \left[\displaystyle \lim_{h\rightarrow 0}\left(\displaystyle \frac{(x+h)}{x}\right)^{\displaystyle \frac{1}{h}}\right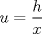]$$ Si $TEX: $u=\displaystyle \frac{h}{x}$$ , entonces $TEX: $h=ux$$ --> $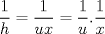TEX: $\displaystyle \frac{1}{h}=\displaystyle \frac{1}{ux}=\displaystyle \frac{1}{u}.\displaystyle \frac{1}{x}$$ $TEX: $Ln\left[ \left( \displaystyle \lim_{h\rightarrow 0}(1+u)^{\displaystyle \frac{1}{u}}\right)^{\displaystyle \frac{1}{x}} \right]$$ usando propiedades de limites se tiene que: 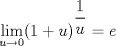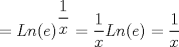$TEX: $\displaystyle \lim_{u\rightarrow 0}(1+u)^{\displaystyle \frac{1}{u}}=e$$ $TEX: $=Ln(e)^{\displaystyle \frac{1}{x}}=\displaystyle \frac{1}{x}Ln(e)=\displaystyle \frac{1}{x}$$ Para $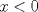TEX: $x<0$$ $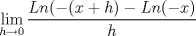TEX: $\displaystyle \lim_{h\rightarrow 0}\displaystyle \frac{Ln(-(x+h)-Ln(-x)}{h}$$ $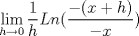TEX: $\displaystyle \lim_{h\rightarrow 0}\displaystyle \frac{1}{h}Ln(\displaystyle \frac{-(x+h)}{-x})$$ $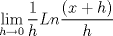TEX: $\displaystyle \lim_{h\rightarrow 0}\displaystyle \frac{1}{h}Ln\displaystyle \frac{(x+h)}{h}$$ que es analogo para la demostracion anterior. Espero este bien... Mensaje modificado por JoNy_SaTiE el Oct 12 2008, 08:14 PM Razón de edición: Tipeo y paréntesis en LaTeX

smaug Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 12 2008, 05:38 PM Publicado: #24
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 145 Registrado: 28-November 07 Desde: valdivia-chiloe Miembro Nº: 13.217 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Hola a todos, me parece que esta bien, es una demostracion entretenida esa, pero la segunda parte esta demás, pues: 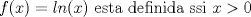$TEX: $f(x)=ln(x)$ esta definida ssi $x>0$$ saludos. -------------------- Ingeniero Civil en Obras Civiles en formación Bachiller en Ciencias de la Ingeniería Universidad Austral de Chile 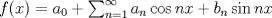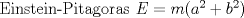$TEX: $f(x)=a_0 + \sum^{\infty}_{n=1} a_{n}\cos {nx} + b_{n}\sin {nx}$$ $TEX: <br />Einstein-Pitagoras<br />$E=m(a^2+b^2)$<br />$

JoNy_SaTiE Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 12 2008, 08:16 PM Publicado: #25
Dios Matemático Supremo Grupo: Colaborador Gold Mensajes: 1.118 Registrado: 11-September 05 Desde: Valdivia/Ancud Miembro Nº: 302 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Para hacer más visible la demostración, edité un par de cosas. Me alegra que se avance aunque sea de a poco. Por cierto, está correcta la demostración. Ahora puedes plantear tu problema, Nicte. -------------------- Comienza a crear documentos con LaTeX. Ya usas LaTeX y quieres aprender un poco más ... pincha aquí Si eres de la UaCH ... únete a la causa !!! J. Jonathan H. Oberreuter A. Universidad Austral de Chile - RWTH Aachen alumni Est. Magister en Acústica y Vibraciones Ingeniero Civil Acústico (E) Bachiller y Licenciado en Cs. de la Ingeniería

Nicte Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 12 2008, 08:58 PM Publicado: #26
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 28 Registrado: 14-April 08 Desde: Valdivia Miembro Nº: 20.061 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	ok... si enrealidad no sabia hacer el parentesis bien. bueno aqui va: 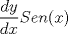$TEX: $\displaystyle\frac{dy}{dx}Sen(x)$$

CuadraoFunk Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 12 2008, 09:36 PM Publicado: #27
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 165 Registrado: 15-October 06 Desde: Santiago Miembro Nº: 2.530 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: <br />\begin{eqnarray}<br />\frac{d}{dx}\sin (x)&=&\underset{h\to 0}{\mathop{\lim }}\,\frac{\sin (x+h)-\sin (x)}{h} \\ <br />&=&\underset{h\to 0}{\mathop{\lim }}\,\frac{\left[ \sin (x)(\cos (h))+\cos (x)(\sin (h)) \right]-\sin (x)}{h} \\ <br />&=&\underset{h\to 0}{\mathop{\lim }}\,\frac{\sin (x)\left[ (\cos (h))-1 \right]+\cos (x)(\sin (h))}{h} \\ <br />&=&\underset{h\to 0}{\mathop{\lim }}\,\left\{ \sin (x)\frac{\left[ (\cos (h))-1 \right]}{h}+\cos (x)\frac{\sin (h)}{h} \right\} \\ <br />&=&\sin (x)\cdot 0+\cos (x)\cdot 1 \\ <br />&=&\cos (x) \\<br />\end{eqnarray} <br />$ Dejo mi problema propuesto altiro: 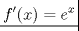$TEX: <br />\begin{eqnarray}<br />\left. {\underline {\, <br /> f'(x)=e^{x} \,}}\! \right\|<br />\end{eqnarray}<br />$ Mensaje modificado por CuadraoFunk el Oct 12 2008, 09:42 PM -------------------- Felipe Ramirez Ingenieria en Aviacion

smaug Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 13 2008, 02:13 PM Publicado: #28
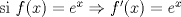Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 145 Registrado: 28-November 07 Desde: valdivia-chiloe Miembro Nº: 13.217 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	imagino que la pregunta es probar que 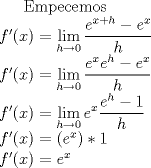$TEX: si $f(x)=e^x \Rightarrow f'(x)= e^x$$ $TEX: Empecemos\\<br />$f'(x)=\displaystyle\lim_{h \to 0}{\frac{e^{x+h}-e^x}{h}}$\\<br />$ f'(x)= \displaystyle\lim_{h \to 0}{\frac{e^{x}e^{h}-e^x}{h}}$\\<br />$ f'(x)= \displaystyle\lim_{h \to 0}{e^x}\frac{e^h-1}{h}$\\<br />$ f'(x)=(e^x)*1$\\<br />$ f'(x)= e^x$<br />$ saludos. -------------------- Ingeniero Civil en Obras Civiles en formación Bachiller en Ciencias de la Ingeniería Universidad Austral de Chile 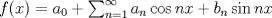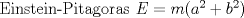$TEX: $f(x)=a_0 + \sum^{\infty}_{n=1} a_{n}\cos {nx} + b_{n}\sin {nx}$$ $TEX: <br />Einstein-Pitagoras<br />$E=m(a^2+b^2)$<br />$

smaug Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 14 2008, 06:47 PM Publicado: #29
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 145 Registrado: 28-November 07 Desde: valdivia-chiloe Miembro Nº: 13.217 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	¿Ta bueno?, ¿puedo plantear mi problema? saludos.. pd: Preparense para la prueba de Fisica 3 del jueves los que esten dando el ramo. -------------------- Ingeniero Civil en Obras Civiles en formación Bachiller en Ciencias de la Ingeniería Universidad Austral de Chile 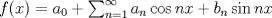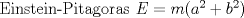$TEX: $f(x)=a_0 + \sum^{\infty}_{n=1} a_{n}\cos {nx} + b_{n}\sin {nx}$$ $TEX: <br />Einstein-Pitagoras<br />$E=m(a^2+b^2)$<br />$

Uchiha Itachi Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 14 2008, 07:39 PM Publicado: #30
Staff FMAT Grupo: Super Moderador Mensajes: 4.857 Registrado: 2-January 08 Miembro Nº: 14.268 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \[<br />\begin{gathered}<br /> {\text{Otra forma de hacer la derivada por definicion de }}f\left( x \right) = \sin x \hfill \\<br /> \boxed{{\text{Solucion :}}} \hfill \\<br /> f'\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{\sin \left( {x + h} \right) - \sin x}}<br />{h} \hfill \\<br /> f'\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{2\sin \left( {\frac{{x + h - x}}<br />{2}} \right)\cos \left( {\frac{{x + h + x}}<br />{2}} \right)}}<br />{h} \hfill \\<br /> f'\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{2\sin \left( {\frac{h}<br />{2}} \right)\cos \left( {\frac{{2x + h}}<br />{2}} \right)}}<br />{h} \hfill \\<br /> f'\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{\sin \left( {\frac{h}<br />{2}} \right)}}<br />{{\frac{h}<br />{2}}} \cdot \cos \left( {x + \frac{h}<br />{2}} \right) \hfill \\<br /> f'\left( x \right) = \left\{ {\mathop {\lim }\limits_{h \to 0} \frac{{\sin \left( {\frac{h}<br />{2}} \right)}}<br />{{\frac{h}<br />{2}}}} \right\} \cdot \left\{ {\mathop {\lim }\limits_{h \to 0} \cos \left( {x + \frac{h}<br />{2}} \right)} \right\} \hfill \\<br /> f'\left( x \right) = 1 \cdot \cos \left( x \right) = \cos \left( x \right) \hfill \\<br /> \hfill \\<br /> \therefore f'\left( x \right) = \cos x \hfill \\<br /> \hfill \\<br /> {\text{Saludos}} \hfill \\ <br />\end{gathered} <br />\]$ -------------------- Candidato a doctor en Cs. De la ingeniería mención modelamiento matemático, DIM. Universidad de Chile Magíster en ciencias mención matemática, Profesor de estado en matemáticas y computación, Licenciado en educación matemáticas y computación, USACH

« Posterior · Cálculo I · Anterior »

10 Páginas:

< 1 2 3 4 5 > »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 4th April 2025 - 02:55 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.