Derivatón Uach - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Austral de Chile > Cálculo I

10 Páginas:

1 2 3 > »

Reply to this topic

Start new topic

Derivatón Uach, versión de prueba

JoNy_SaTiE Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 28 2008, 02:12 PM Publicado: #1
Dios Matemático Supremo Grupo: Colaborador Gold Mensajes: 1.118 Registrado: 11-September 05 Desde: Valdivia/Ancud Miembro Nº: 302 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Fmatianos: Damos comienzo a la primera Derivatón de nuestro sector Uach. Las reglas de esta maratónica actividad son las siguientes: 0.- El objetivo de esta actividad es aprender a realizar derivaciones por definición y por reglas de derivación. Además, problemas de aplicación pueden ser incluidos. 1.- Pueden participar todos los estudiantes de la Universidad Austral de Chile (y de otros colegios y universidades). 2.- La estructura de la Derivatón es la siguiente: 2.0- Los problemas planteados deben ser enumerados. 2.1.- Se planteará una función de una variable, la cual deberá ser derivada por reglas de derivación, según el problema. Sólo se derivarán por definición algunas funciones elementales. 2.2.- Se exige un desarrollo ordenado y explicativo sobre cómo se llegó a la solución. Establecer dominios y recorridos puede resultar también productivo. 2.3.- El problema de derivación quedará resuelto cuando el autor del problema (o el moderador) quede conforme con la respuesta, pudiendo hacer acotaciones sobre la solución. 2.4.- Quien resuelva el problema de manera satisfactoria, planteará el próxima problema. 3.- Los problemas y soluciones DEBEN ser posteadas en LaTeX (Ver sector Comunidad-Manuales). 4.- No se aceptarán posts fuera del contexto de la Derivatón. 5.- Por último, esta actividad no está dirigida a la competencia, sino al aprendizaje. 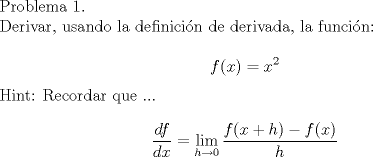$TEX: Problema 1.<br /><br />Derivar, usando la definición de derivada, la función:<br /><br />$$ f(x)=x^2$$<br /><br />Hint: Recordar que ...<br /><br />$$ \dfrac{df}{dx}=\lim_{h\to 0}\dfrac{f(x+h)-f(x)}{h}$$<br />$ -------------------- Comienza a crear documentos con LaTeX. Ya usas LaTeX y quieres aprender un poco más ... pincha aquí Si eres de la UaCH ... únete a la causa !!! J. Jonathan H. Oberreuter A. Universidad Austral de Chile - RWTH Aachen alumni Est. Magister en Acústica y Vibraciones Ingeniero Civil Acústico (E) Bachiller y Licenciado en Cs. de la Ingeniería

xure Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 28 2008, 02:43 PM Publicado: #2
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 167 Registrado: 25-September 07 Desde: PAC Miembro Nº: 10.556 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: toy recien empesando espero que este bien <br />$ $TEX: \[<br />\begin{gathered}<br /> \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {x + h} \right) - f\left( x \right)}}<br />{h} \Rightarrow \mathop {\lim }\limits_{h \to 0} \frac{{\left( {x + h} \right)^2 - x^2 }}<br />{h} \hfill \\<br /> \mathop {\lim }\limits_{h \to 0} \frac{{x^2 + 2xh + h^2 - x^2 }}<br />{h} \hfill \\<br /> \mathop {\lim }\limits_{h \to 0} \frac{{2xh + h^2 }}<br />{h} = \mathop {\lim }\limits_{h \to 0} \frac{{h\left( {2x + h} \right)}}<br />{h} = \mathop {\lim }\limits_{h \to 0} 2x + h \hfill \\<br /> \therefore f' = 2x \hfill \\ <br />\end{gathered} <br />\]<br />$ --------------------

danielomalmsteen Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 28 2008, 02:43 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.413 Registrado: 13-March 08 Desde: Al frente del mundo Magico Miembro Nº: 16.846 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \[<br />\begin{gathered}<br /> \frac{{df}}<br />{{dx}} = \frac{{\left( {x + h} \right)^2 - x^2 }}<br />{h} \hfill \\<br /> \frac{{df}}<br />{{dx}} = \frac{{x^2 + 2xh + h^2 - x^2 }}<br />{h} \hfill \\<br /> \frac{{df}}<br />{{dx}} = \frac{{2xh + h^2 }}<br />{h} \hfill \\<br /> \frac{{df}}<br />{{dx}} = \frac{{h\left( {2x + h} \right)}}<br />{h} \hfill \\<br /> \frac{{df}}<br />{{dx}} = 2x + h \hfill \\<br /> \boxed{\frac{{df}}<br />{{dx}} = 2x} \hfill \\ <br />\end{gathered} <br />\]<br />$ mi aporte xD --------------------

dalomismo... Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 28 2008, 04:13 PM Publicado: #4
Maestro Matemático Grupo: Usuario FMAT Mensajes: 128 Registrado: 18-March 08 Desde: Valdivia y varias partes que sinceramente no te debería importar XD Miembro Nº: 17.202 Nacionalidad: Universidad: Sexo:	y su ejercicio??? -------------------- Estudiante de Ingeniería Civil Acústica Universidad Austral de Chile CITA “Las matemáticas son la música de la razón” James Joseph Silvestre (1814-1897). Matemático británico. “El álgebra es generosa: a menudo da más de lo que se le pide” D’Alembert (1717-1783). Matemático y filósofo francés. “La música es la aritmética de los sonidos, como la óptica es la geometría de la luz.” Claude Debussy (1862-1918) Compositor Francés “La música es un ejercicio aritmético ocultado del alma, que no sabe que está contando.” “La música es el placer que experimenta la mente humana al contar sin darse cuenta de que está contando.” Gottfried Wilhelm Leibniz(1646-1716). Filósofo y Matemático alemán. Un país que no investiga es un país que no progresa MySpace de Azotth MySpace de Denun

JoNy_SaTiE Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 28 2008, 04:41 PM Publicado: #5
Dios Matemático Supremo Grupo: Colaborador Gold Mensajes: 1.118 Registrado: 11-September 05 Desde: Valdivia/Ancud Miembro Nº: 302 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(xure @ Sep 28 2008, 02:33 PM) $TEX: toy recien empesando espero que este bien <br />$ $TEX: \[<br />\begin{gathered}<br /> \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {x + h} \right) - f\left( x \right)}}<br />{h} \Rightarrow \mathop {\lim }\limits_{h \to 0} \frac{{\left( {x + h} \right)^2 - x^2 }}<br />{h} \hfill \\<br /> \mathop {\lim }\limits_{h \to 0} \frac{{x^2 + 2xh + h^2 - x^2 }}<br />{h} \hfill \\<br /> \mathop {\lim }\limits_{h \to 0} \frac{{2xh + h^2 }}<br />{h} = \mathop {\lim }\limits_{h \to 0} \frac{{h\left( {2x + h} \right)}}<br />{h} = \mathop {\lim }\limits_{h \to 0} 2x + h \hfill \\<br /> \therefore f' = 2x \hfill \\ <br />\end{gathered} <br />\]<br />$ Se ganó el primer punto. CITA(danielomalmsteen @ Sep 28 2008, 02:33 PM) $TEX: \[<br />\begin{gathered}<br /> \frac{{df}}<br />{{dx}} = \frac{{\left( {x + h} \right)^2 - x^2 }}<br />{h} \hfill \\<br /> \frac{{df}}<br />{{dx}} = \frac{{x^2 + 2xh + h^2 - x^2 }}<br />{h} \hfill \\<br /> \frac{{df}}<br />{{dx}} = \frac{{2xh + h^2 }}<br />{h} \hfill \\<br /> \frac{{df}}<br />{{dx}} = \frac{{h\left( {2x + h} \right)}}<br />{h} \hfill \\<br /> \frac{{df}}<br />{{dx}} = 2x + h \hfill \\<br /> \boxed{\frac{{df}}<br />{{dx}} = 2x} \hfill \\ <br />\end{gathered} <br />\]<br />$ mi aporte xD Faltó el desarrollo con límites. Ahora falta que xure postee su problema. -------------------- Comienza a crear documentos con LaTeX. Ya usas LaTeX y quieres aprender un poco más ... pincha aquí Si eres de la UaCH ... únete a la causa !!! J. Jonathan H. Oberreuter A. Universidad Austral de Chile - RWTH Aachen alumni Est. Magister en Acústica y Vibraciones Ingeniero Civil Acústico (E) Bachiller y Licenciado en Cs. de la Ingeniería

xure Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 28 2008, 04:46 PM Publicado: #6
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 167 Registrado: 25-September 07 Desde: PAC Miembro Nº: 10.556 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	P2.- calcular la derivada por definicion de: $TEX: \[<br />f(x) = 2x^2 + 3<br />\]<br />$ --------------------

Rattlehead_ Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 28 2008, 04:59 PM Publicado: #7
Dios Matemático Grupo: Usuario FMAT Mensajes: 428 Registrado: 19-July 07 Desde: Ñuñoa Miembro Nº: 7.679 Nacionalidad: Universidad: Sexo:	CITA(xure @ Sep 28 2008, 07:36 PM) calcular la derivada por definicion de: $TEX: \[<br />f(x) = 2x^2 + 3<br />\]<br />$ $TEX: <br />\[<br />\begin{gathered}<br /> \frac{{df}}<br />{{dx}} = \mathop {\lim }\limits_{h \to 0} \frac{{f(x + h) - f(x)}}<br />{h} = \mathop {\lim }\limits_{h \to 0} \frac{{2(x + h)^2 + 3 - (2x^2 + 3)}}<br />{h} \hfill \\<br /> = \mathop {\lim }\limits_{h \to 0} \frac{{2x^2 + 4xh + 2h^2 + 3 - 2x^2 - 3}}<br />{h} = \mathop {\lim }\limits_{h \to 0} \frac{{4xh + 2h^2 }}<br />{h} = \mathop {\lim }\limits_{h \to 0} 4x + 2h \hfill \\<br /> = 4x + 0 = 4x \hfill \\<br /> \hfill \\<br /> \therefore f' = 4x \hfill \\ <br />\end{gathered} <br />\]$ Espero confirmacion, para poner un problema Saludos -------------------- "Las Matematicas son el alfabeto con el cual Dios ha escrito el universo"

deixo Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 28 2008, 05:10 PM Publicado: #8
Dios Matemático Supremo Grupo: Baneado Mensajes: 1.737 Registrado: 6-September 07 Miembro Nº: 9.900	que entretenido!!, yo también queroo!!

xure Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 28 2008, 05:15 PM Publicado: #9
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 167 Registrado: 25-September 07 Desde: PAC Miembro Nº: 10.556 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Metal Militia @ Sep 28 2008, 05:50 PM) $TEX: <br />\[<br />\begin{gathered}<br /> \frac{{df}}<br />{{dx}} = \mathop {\lim }\limits_{h \to 0} \frac{{f(x + h) - f(x)}}<br />{h} = \mathop {\lim }\limits_{h \to 0} \frac{{2(x + h)^2 + 3 - (2x^2 + 3)}}<br />{h} \hfill \\<br /> = \mathop {\lim }\limits_{h \to 0} \frac{{2x^2 + 4xh + 2h^2 + 3 - 2x^2 - 3}}<br />{h} = \mathop {\lim }\limits_{h \to 0} \frac{{4xh + 2h^2 }}<br />{h} = \mathop {\lim }\limits_{h \to 0} 4x + 2h \hfill \\<br /> = 4x + 0 = 4x \hfill \\<br /> \hfill \\<br /> \therefore f' = 4x \hfill \\ <br />\end{gathered} <br />\]$ Espero confirmacion, para poner un problema Saludos Exeltente, ponga su problema numa --------------------

Rattlehead_ Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 28 2008, 05:18 PM Publicado: #10
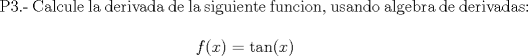
Dios Matemático Grupo: Usuario FMAT Mensajes: 428 Registrado: 19-July 07 Desde: Ñuñoa Miembro Nº: 7.679 Nacionalidad: Universidad: Sexo:	Ya , uno facil y didactico para comenzar: $TEX: <br />P3.- Calcule la derivada de la siguiente funcion, usando algebra de derivadas:<br /><br />$$f(x)=\tan(x)$$$ -------------------- "Las Matematicas son el alfabeto con el cual Dios ha escrito el universo"

« Posterior · Cálculo I · Anterior »

10 Páginas:

1 2 3 > »

Reply to this topic

Start new topic

2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 05:27 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.