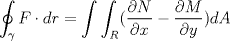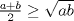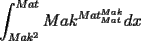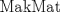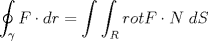Cuarto Nivel Individual

Cuarto Nivel Individual, Santiago, etc

CyedqD Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 27 2008, 08:39 PM Publicado: #1
Coordinador General Gran Maraton PSU Final 2008 Grupo: Moderador Mensajes: 1.607 Registrado: 11-June 07 Desde: Peñalolen, Stgo Miembro Nº: 6.641 Nacionalidad: Universidad: Sexo:	$TEX: \textsf{Quinta Fecha \ - \ 27 de Septiembre del 2008 \ - \ Cuarto Nivel}$ $TEX: \noindent \textbf{1.} \textsf{Probar que no hay cuatro numeros naturales consecutivos tales que se multiplicacion sea un numero natural al cuadrado.}$ $TEX: \noindent \textbf{2.} \textsf{Sean $\Gamma _1$ y $\Gamma _2$ dos circunferencias secantes en los puntos $Q$ y $R$. Sea $P$ un punto perteneciente al segmento $QR$, y sea $L$ una recta que pasa por $P$ con $L \ne QR$; tal que $L$ corta $\Gamma _1$ en $A$ y $C$, y $L$ corta a $\Gamma _2$ en $B$ y $D$; tales que en $L$ los puntos queden en el orden $A-B-P-C-D$.}\\<br /><br />\noindent \textsf{Demuestre que} $$\dfrac{{AP}}{{BP}} = \frac{{AD}}{{BC}}$$$ --------------------

Felipe_ambuli Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 27 2008, 09:57 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad: Sexo:	$TEX: \noindent Notemos que $QR$ es eje radical de $\Gamma_1$ y $\Gamma_2$ entonces por potencia de $P$ sobre $\Gamma_1$ se tiene que $AP\cdot PC=QP\cdot PR$ y por potencia de $P$ sobre $\Gamma_2$ se tiene $BP\cdot PD=QP\cdot QR$ de donde se sigue que $AP\cdot PC=BP\cdot PD\Rightarrow \dfrac{PD}{AP}=\dfrac{PC}{BP}\Rightarrow \dfrac{AD-AP}{AP}=\dfrac{BC-BP}{BP}\Rightarrow \dfrac{AD}{AP}=\dfrac{BC}{BP}\Rightarrow \dfrac{AP}{AD}=\dfrac{BP}{BC}\Rightarrow \dfrac{AP}{BP}=\dfrac{AD}{BC}$ y listo.$

CyedqD Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 27 2008, 09:59 PM Publicado: #3
Coordinador General Gran Maraton PSU Final 2008 Grupo: Moderador Mensajes: 1.607 Registrado: 11-June 07 Desde: Peñalolen, Stgo Miembro Nº: 6.641 Nacionalidad: Universidad: Sexo:	CITA(Felipe_ambuli @ Sep 27 2008, 10:47 PM) $TEX: \noindent Notemos que $QR$ es eje radical de $\Gamma_1$ y $\Gamma_2$ entonces por potencia de $P$ sobre $\Gamma_1$ se tiene que $AP\cdot PC=QP\cdot PR$ y por potencia de $P$ sobre $\Gamma_2$ se tiene $BP\cdot PD=QP\cdot QR$ de donde se sigue que $AP\cdot PC=BP\cdot PD\Rightarrow \dfrac{PD}{AP}=\dfrac{PC}{BP}\Rightarrow \dfrac{AD-AP}{AP}=\dfrac{BC-BP}{BP}\Rightarrow \dfrac{AD}{AP}=\dfrac{BC}{BP}\Rightarrow \dfrac{AP}{AD}=\dfrac{BP}{BC}\Rightarrow \dfrac{AP}{BP}=\dfrac{AD}{BC}$ y listo.$ Y listo, el problema moria asi de simple xD --------------------

p.j.t Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 27 2008, 10:09 PM Publicado: #4
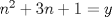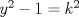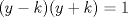Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 766 Registrado: 6-May 07 Desde: San Pedro de la Paz, Concepción Miembro Nº: 5.639 Nacionalidad: Colegio/Liceo: Sexo:	P1 $TEX: $n(n+1)(n+2)(n+3)=[n(n+3)][(n+1)(n+2)]=[n^2+3n][n^2+3n+2]=(n^2+3n)^2+2(n^2+3n)=(n^2+3n+1)^2-1$$ Sea $TEX: $n^2+3n+1=y$$ . 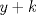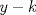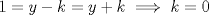Luego necesitamos que para algun k se cumpla: $TEX: $y^2-1=k^2$$ $TEX: $(y-k)(y+k)=1$$ Como y,k son naturales, entonces $TEX: $y+k$$ es positivo, por lo que $TEX: $y-k$$ tambien lo es y como ambos dividen a 1, entonces ambos deben ser 1 $TEX: $1=y-k=y+k \implies k=0$$ Pero la expresion entonces no sería cuadrado de un natural... por lo que no es posible que el producto sea cuadrado perfecto salu2 -------------------- asdf

makmat Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 27 2008, 11:07 PM Publicado: #5
Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo: Universidad: Sexo:	excelente respuesta pjt y felipe , los felicito -------------------- $TEX: $displaystyle oint _{gamma} F cdot dr = displaystyle int int_{R} (dfrac{partial N}{partial x} - dfrac{partial M}{partial y}) dA$$ $TEX: $frac{a+b}{2}ge sqrt{ab}$$ [!] $TEX: $displaystyle int_{Mak^2}^{Mat}Mak^{Mat^{Mak}_{Mat}}dx$$ Doctor en Matemáticas Estudiando y creando problemas $TEX: MakMat$ $TEX: $displaystyle oint_{gamma} F cdot dr= int int_{R} rot F cdot black{N} dS$$ Adiós Kazajstán...

Gaston Burrull	Oct 18 2008, 08:30 PM Publicado: #6
Invitado	me compliqué demasiado en la primera.. demostré varias cosas y fui descartando.. pero ese método algebraico está mucho mejor...

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 6th March 2025 - 09:32 PM