|
|
|
|
|
|
|
  |
 Sep 21 2008, 07:24 PM Sep 21 2008, 07:24 PM
Publicado:
#1
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
23ª OLIMPIADA IBEROAMERICANA DE MATEMÁTICAS Salvador, BA, Brasil, 2008 Primera Prueba: Martes 23 de Septiembre Problema 1: Considere los números  distribuidos en un tablero de distribuidos en un tablero de 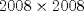 , de modo que en cada casilla haya un número distinto. Para cada fila y cada columna del tablero se calcula la diferencia entre el mayor y el menor de sus elementos. Sea , de modo que en cada casilla haya un número distinto. Para cada fila y cada columna del tablero se calcula la diferencia entre el mayor y el menor de sus elementos. Sea 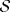 la suma de los la suma de los  números obtenidos. Determine el mayor valor posible de números obtenidos. Determine el mayor valor posible de 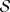 . .Problema 2: Sean 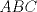 un triángulo escaleno y un triángulo escaleno y 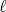 la bisectriz exterior del la bisectriz exterior del 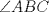 . Sean . Sean 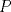 y y 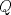 los pies de las perpendiculares a la recta los pies de las perpendiculares a la recta 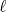 que pasan por que pasan por 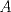 y y 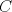 , respectivamente. Sean , respectivamente. Sean 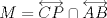 y y 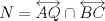 . Pruebe que las rectas . Pruebe que las rectas 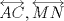 y y 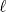 tienen un punto en común. tienen un punto en común. Problema 3: Sean  y y  números enteros tales que el polinomio números enteros tales que el polinomio 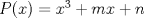 tiene la siguiente propiedad: si tiene la siguiente propiedad: si  e e 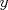 son enteros y son enteros y 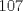 divide a divide a 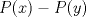 , entonces , entonces 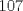 divide a divide a 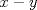 . Demuestre que . Demuestre que 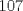 divide a divide a  . . Segunda Prueba: Miércoles 24 de Septiembre Problema 4: Pruebe que la ecuación 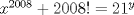 no tiene soluciones enteras 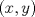 . .Problema 5: Sean 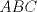 un triángulo y un triángulo y 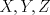 puntos interiores de los lados puntos interiores de los lados 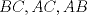 respectivamente. Sean respectivamente. Sean 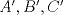 los circuncentros correspondientes a los triángulos los circuncentros correspondientes a los triángulos 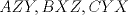 , respectivamente. Demuestre que: , respectivamente. Demuestre que: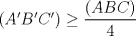 y que la igualdad ocurre si y sólo si 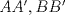 y y 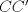 son concurrentes. son concurrentes.Nota: Para un triángulo cualquiera 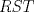 , denotamos su área por , denotamos su área por 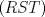 . . Problema 6: En un partido de biribol se enfrentan dos equipos de cuatro jugadores cada uno. Se organiza un torneo de biribol en el que participan  personas, que forman equipos para cada partido (los equipos no son fijos). Al final del torneo se observó que cada dos personas disputaron exactamente un partido en equipos rivales. Determinar para qué valores de personas, que forman equipos para cada partido (los equipos no son fijos). Al final del torneo se observó que cada dos personas disputaron exactamente un partido en equipos rivales. Determinar para qué valores de  es posible organizar un torneo con tales características. es posible organizar un torneo con tales características.Resumen de soluciones -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Sep 23 2008, 10:41 PM Sep 23 2008, 10:41 PM
Publicado:
#2
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 2: Sean 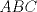 un triángulo escaleno y un triángulo escaleno y 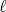 la bisectriz exterior del la bisectriz exterior del 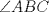 . Sean . Sean 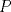 y y 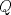 los pies de las perpendiculares a la recta los pies de las perpendiculares a la recta 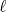 que pasan por que pasan por 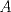 y y 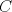 , respectivamente. Sean , respectivamente. Sean 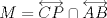 y y 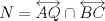 . Pruebe que las rectas . Pruebe que las rectas 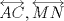 y y 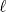 tienen un punto en común. tienen un punto en común.Solución al problema 2   Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Sep 23 2008, 10:46 PM Sep 23 2008, 10:46 PM
Publicado:
#3
|
|
 Coordinador General Gran Maraton PSU Final 2008 Grupo: Moderador Mensajes: 1.607 Registrado: 11-June 07 Desde: Peñalolen, Stgo Miembro Nº: 6.641 Nacionalidad:  Universidad:  Sexo:  |
--------------------  |
|
|
|
 Sep 23 2008, 11:00 PM Sep 23 2008, 11:00 PM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
Solución al problema 2   Saludos Quisas me ganaron, pero para concluir que 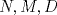 colineales, bastaba mostrar que colineales, bastaba mostrar que 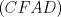 es armonica, y eso se sigue del lema 2 del adjunto (me apoyo en el lema 1 y 2). es armonica, y eso se sigue del lema 2 del adjunto (me apoyo en el lema 1 y 2). harmonic_division.pdf ( 145.39k )
Número de descargas: 94
harmonic_division.pdf ( 145.39k )
Número de descargas: 94 |
|
|
|
 Sep 23 2008, 11:00 PM Sep 23 2008, 11:00 PM
Publicado:
#5
|
|
 Coordinador General Gran Maraton PSU Final 2008 Grupo: Moderador Mensajes: 1.607 Registrado: 11-June 07 Desde: Peñalolen, Stgo Miembro Nº: 6.641 Nacionalidad:  Universidad:  Sexo:  |
Quisas me ganaron, pero para concluir que 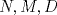 colineales, bastaba mostrar que colineales, bastaba mostrar que 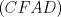 es armonica, y eso se sigue del lema 2 del adjunto (me apoyo en el lema 1 y 2). es armonica, y eso se sigue del lema 2 del adjunto (me apoyo en el lema 1 y 2). harmonic_division.pdf ( 145.39k )
Número de descargas: 94
harmonic_division.pdf ( 145.39k )
Número de descargas: 94Precisamente en algo de eso me base para mi solucion. Buen pdf ese, aprendi harto de ahi. --------------------  |
|
|
|
 Sep 24 2008, 04:17 PM Sep 24 2008, 04:17 PM
Publicado:
#6
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
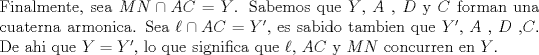 Disculpa, pero, ¿qué es una cuaterna armónica? ¿Por qué "sabemos" que Y, A, D, C y Y', A, D, C son cuaternas armónicas? ¿Viene en el enunciado, o se deduce de alguna parte? No entiendo esa parte, agradecería que me aclararas. De antemano, gracias Saludos. PD: todo esto un corrector exigente, como los de las Ibero, se lo preguntaría. -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Sep 24 2008, 07:25 PM Sep 24 2008, 07:25 PM
Publicado:
#7
|
|
 Coordinador General Gran Maraton PSU Final 2008 Grupo: Moderador Mensajes: 1.607 Registrado: 11-June 07 Desde: Peñalolen, Stgo Miembro Nº: 6.641 Nacionalidad:  Universidad:  Sexo:  |
Disculpa, pero, ¿qué es una cuaterna armónica? ¿Por qué "sabemos" que Y, A, D, C y Y', A, D, C son cuaternas armónicas? ¿Viene en el enunciado, o se deduce de alguna parte? No entiendo esa parte, agradecería que me aclararas. De antemano, gracias Saludos. PD: todo esto un corrector exigente, como los de las Ibero, se lo preguntaría. Por cuaterna armonica me refiero a que los punto indicados estan verifican la proporcion armonica, o sea ![TEX: \[<br />\frac{{DC}}<br />{{AD}} = \frac{{YC}}<br />{{YA}}<br />\]](./tex/1aae362a6a8d710239f39b0403e45096.png) Lo otro viene de que  .asdasd.PNG ( 13.62k )
Número de descargas: 3
.asdasd.PNG ( 13.62k )
Número de descargas: 3En la figura si D es el conjugado armonico de B respecto al segmento CA, entonces F, E y D son colineales. Sin embargo el reciproco tambien es cierto (o sea si F, E y D son colineales, D es el conjugado armonico de B) pues el punto D es unico. Y fue el reciproco de este teorema el que use para la solucion. Mas que nada te agradezco por la correccion, pues no se bien que como evaluan las respuestas en estas pruebas, y que cosas se pueden tomar como evidentes y que cosas no --------------------  |
|
|
|
 Sep 25 2008, 05:49 PM Sep 25 2008, 05:49 PM
Publicado:
#8
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad:  Colegio/Liceo:  Sexo:  |
 PD: esto es un post data --------------------  |
|
|
|
 Sep 25 2008, 08:14 PM Sep 25 2008, 08:14 PM
Publicado:
#9
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 4: Pruebe que la ecuación 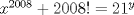 no tiene soluciones enteras 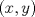 . .pelao me ganó ¬¬, pero igual posteo mi solución que es parecida (lo había sacado en la mañana pero llegué tarde a mi casa Solución al problema 4  Saludos. -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Sep 25 2008, 09:57 PM Sep 25 2008, 09:57 PM
Publicado:
#10
|
|
|
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 20 Registrado: 9-May 06 Miembro Nº: 1.055 |
wena! me keo kn la solucion de killua
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 11:18 AM |












