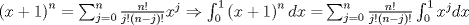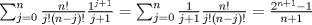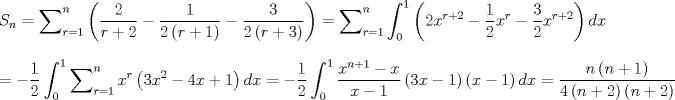|
|
|
|
|
|
|
  |
 Jun 25 2006, 03:18 PM Jun 25 2006, 03:18 PM
Publicado:
#11
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 743 Registrado: 23-November 05 Desde: Mi Humilde Hogar! Miembro Nº: 394 Nacionalidad:  Universidad:  Sexo:  |
Bueno aqui aportare con 1
![TEX: <br />\[<br />\displaystyle\sum\limits_{k = 1}^n {\dfrac{{2k + 1}}{{k^2 \left( {k + 1} \right)^2 }}} <br />\]<br />](./tex/100348.gif) Solucion: --------------------  © Ingeniero Civil Metalurgico. ![TEX: [<br />psi psi psi .oint {mathfrak{M}alpha dag .mathbb{C}ell } <br />]](./tex/1177613368.gif) "...La Felicidad es una mariposa que, si la persigues, siempre está justo más alla de tu alcance; Sin embargo, si te sentaras en silencio, podria posarse sobre ti..." |
|
|
|
 Jun 25 2006, 06:09 PM Jun 25 2006, 06:09 PM
Publicado:
#12
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 228 Registrado: 8-August 05 Desde: Santiago de Chile Miembro Nº: 194 |
  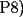 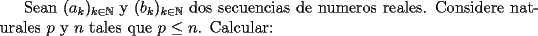 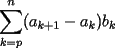 |
|
|
|
 Jun 25 2006, 07:49 PM Jun 25 2006, 07:49 PM
Publicado:
#13
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 228 Registrado: 8-August 05 Desde: Santiago de Chile Miembro Nº: 194 |
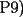  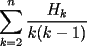 |
|
|
|
 Jul 27 2006, 09:07 PM Jul 27 2006, 09:07 PM
Publicado:
#14
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 743 Registrado: 23-November 05 Desde: Mi Humilde Hogar! Miembro Nº: 394 Nacionalidad:  Universidad:  Sexo:  |
![TEX: \[<br />S = \sum\limits_{i = 1}^n {(i - 1)} <br />\]](./tex/100359.gif) Solucion: PD: Como hago para que el signo igual salga bien, asi como en el ejemplo 9??? --------------------  © Ingeniero Civil Metalurgico. ![TEX: [<br />psi psi psi .oint {mathfrak{M}alpha dag .mathbb{C}ell } <br />]](./tex/1177613368.gif) "...La Felicidad es una mariposa que, si la persigues, siempre está justo más alla de tu alcance; Sin embargo, si te sentaras en silencio, podria posarse sobre ti..." |
|
|
|
 Jul 27 2006, 11:37 PM Jul 27 2006, 11:37 PM
Publicado:
#15
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 365 Registrado: 27-May 05 Desde: Puente Asalto, Santiago Miembro Nº: 68 Nacionalidad:  Colegio/Liceo:  Sexo:  |
CITA(Killua @ Jun 6 2006, 03:36 PM) Veamos... 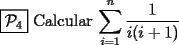 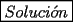 Saludos Aplicando la Telescópica este problema sale más rapidito.. ya que 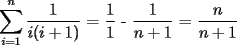 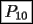 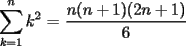 Solución --------------------  |
|
|
|
 Jul 27 2006, 11:57 PM Jul 27 2006, 11:57 PM
Publicado:
#16
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 903 Registrado: 28-May 05 Desde: Santiago, Chile Miembro Nº: 69 Nacionalidad:  Colegio/Liceo:  Sexo:  |
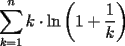 Solución -------------------- Bachiller en Ciencias
(ex) Estudiante de Medicina Estudiante de Ingeniería Civil de Industrias, diploma en Ingeniería Matemática Pontificia Universidad Católica de Chile  |
|
|
|
 Jul 28 2006, 02:24 PM Jul 28 2006, 02:24 PM
Publicado:
#17
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
 -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 May 21 2011, 09:35 PM May 21 2011, 09:35 PM
Publicado:
#18
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 537 Registrado: 13-June 10 Desde: Linares Miembro Nº: 72.473 Nacionalidad:  Sexo:  |
quiero aportar con una también :B
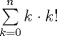 Solución: -------------------- |
|
|
|
| master_c |
 May 21 2011, 10:18 PM May 21 2011, 10:18 PM
Publicado:
#19
|
|
Invitado |
Calcular
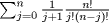 Mensaje modificado por master_c el May 21 2011, 10:19 PM |
|
|
|
| master_c |
 May 21 2011, 10:35 PM May 21 2011, 10:35 PM
Publicado:
#20
|
|
Invitado |
Calcular
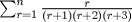 |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 6th March 2025 - 09:54 PM |





![TEX: <br />\[<br />{2k + 1}<br />\]<br />](./tex/100349.gif) conveniente se tiene:
conveniente se tiene:![TEX: <br />\[<br />\begin{array}{l}<br /> \displaystyle\sum\limits_{k = 1}^n {\dfrac{{2k + 1}}{{k^2 \left( {k + 1} \right)^2 }}} \\ <br /> \\ <br /> = \displaystyle\sum\limits_{k = 1}^n {\dfrac{{\left( {k + 1} \right)^2 - k^2 }}{{k^2 \left( {k + 1} \right)^2 }}} \\ <br /> \\ <br /> = \displaystyle\sum\limits_{k = 1}^n {\left[ {\dfrac{{\left( {k + 1} \right)^2 }}{{k^2 \left( {k + 1} \right)^2 }} - \dfrac{{k^2 }}{{k^2 \left( {k + 1} \right)^2 }}} \right]} \\ <br /> \\ <br /> = \displaystyle\sum\limits_{k = 1}^n {\left[ {\dfrac{1}{{k^2 }} - \dfrac{1}{{\left( {k + 1} \right)^2 }}} \right]} \\ <br /> \\ <br /> = \displaystyle\sum\limits_{k = 1}^n {\dfrac{1}{{k^2 }}} - \displaystyle\sum\limits_{k = 1}^n {\dfrac{1}{{\left( {k + 1} \right)^2 }}} \\ <br /> \\ <br /> = \left[ {\left( {\dfrac{1}{{1^2 }} - \dfrac{1}{{2^2 }}} \right) + \left( {\dfrac{1}{{2^2 }} - \dfrac{1}{{3^2 }}} \right) + \left( {\dfrac{1}{{3^2 }} - \dfrac{1}{{4^2 }}} \right) + ... - \dfrac{1}{{\left( {n + 1} \right)^2 }}} \right] \\ <br /> \\ <br /> = 1 - \dfrac{1}{{\left( {n + 1} \right)^2 }} \\ <br /> \end{array}<br />\]<br /><br />](./tex/100350.gif)





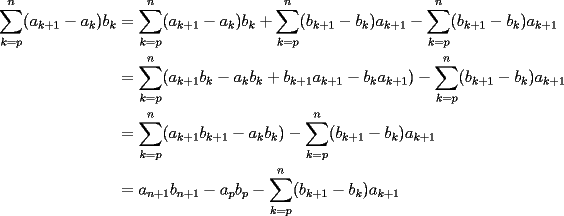
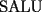
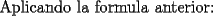
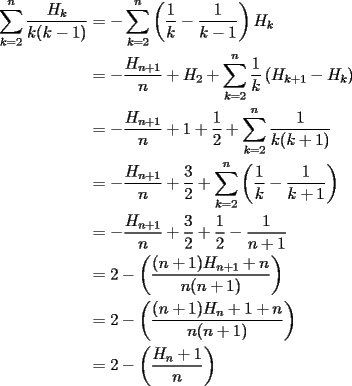
![TEX: \[<br />u = i - 1<br />\]](./tex/100361.gif)
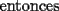
![TEX: \[<br />i = 1,2,....,n \Rightarrow u = 0,1,2,3...,\left( {n - 1} \right),<br />\]](./tex/100363.gif)
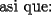
![TEX: \[<br />\begin{gathered}<br /> S = \sum\limits_{u = 0}^{n - 1} u \\ <br /> = \sum\limits_{u = 1}^{n - 1} u \\ <br /> = \frac{{\left( {n - 1} \right)\left( {n - 1 + 1} \right)}}<br />{2} \\ <br /> = \frac{{\left( {n - 1} \right)n}}<br />{2} \\ <br />\end{gathered} <br />\]](./tex/100365.gif)
![TEX: \[<br />\begin{gathered}<br /> S = \sum\limits_{i = 1}^n {(i - 1)} \\ <br /> = \sum\limits_{i = 1}^n i - \sum\limits_{i = 1}^n 1 \\ <br /> = \frac{{n\left( {n + 1} \right)}}<br />{2} - n \\ <br /> = \frac{{n^2 + n - 2n}}<br />{2} \\ <br /> = \frac{{n\left( {n - 1} \right)}}<br />{2} \\ <br />\end{gathered} <br />\]](./tex/100366.gif)


![TEX: Sabemos que [aplicandole propiedad telescopica]:](./tex/100589.gif)
![TEX: $\displaystyle\sum_{k=1}^{n}{\left[k^3 - (k-1)^3\right]}$ = $n^3 - (1-1)^3=n^3$](./tex/100590.gif)
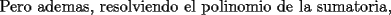
![TEX: $\displaystyle\sum_{k=1}^{n}{\left[k^3 - (k-1)^3\right]}$ = $\displaystyle\sum_{k=1}^{n}{\left[3k^2-3k+1\right]}$](./tex/100592.gif)
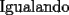
![TEX: $\displaystyle\sum_{k=1}^{n}{\left[3k^2-3k+1\right]}$ = $n^3$](./tex/100594.gif)
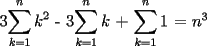
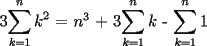
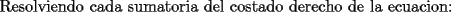
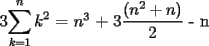
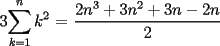
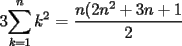
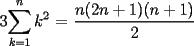
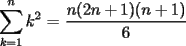
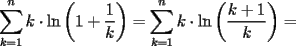
![TEX: $=\displaystyle\sum_{k=1}^{n}\left[k\cdot \ln(k+1)-k\cdot \ln(k)\right]=\displaystyle\sum_{k=1}^{n}\left[(k+1)\cdot \ln(k+1)-\ln(k+1)-k\cdot \ln(k)\right]=$](./tex/100609.gif)
![TEX: $=\displaystyle\sum_{k=1}^{n}\left[(k+1)\cdot \ln(k+1)-k\cdot \ln(k)\right]-\displaystyle\sum_{k=1}^{n}\ln(k+1)=$](./tex/100613.gif)
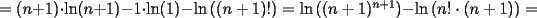
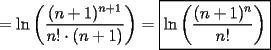

![TEX: \noindent<br />Considere la matriz cuadrada $\displaystyle P=\{p_{i,j}\}_{i,j=1}^n=\{ij\}_{i,j=1}^n$ y llamemos $S_n'$ a la suma de sus elementos\\<br />Definimos la funcion $\displaystyle f: \{a_{i,j}\}_{i,j=1}^m\rightarrow \{2,3,...,2m\}$ como\\<br />$\displaystyle f(a_{i,j})=i+j$. \\<br />No es dificil darse cuenta los elementos de una matriz\\<br />$\displaystyle A=\{a_{i,j}\}_{i,j=1}^m$\\<br />que cumplen $f(a_{i,j})=t$ son los que estan dispuestos diagonalmente en el lugar correspondiente a los elementos de otra matriz $B=\{b_{u,v}\}_{u,v=1}^{2m}$, que pertenecen al cuadrante definido por $1\le u,v\le m$ y que estan sobre la diagonal que va desde $b_{1,t-1}$ hasta $b_{t-1,1}$.\\<br />Notemos que estas diagonales son disjuntas.\\<br />Por lo anterior\\<br />$\displaystyle S_n=\sum_{k=2}^{2n}p_{i,j}:f(p_{i,j})=k\\<br />\Rightarrow S_n=\sum_{p_{i,j}\in P}p_{i,j}=S_n'$\\<br />Asi que basta encontrar $S_n'$. Esto lo haremos sumando los elementos de cada fila y luego sumando todas las sumas obtenidas;\\<br />$\displaystyle S_n=S_n'=\sum_{i=1}^{n}\sum_{j=1}^{n}ij=<br />\sum_{i=1}^{n}i\sum_{j=1}^{n}j=<br />\sum_{i=1}^{n}\frac{n(n+1)}{2}i=\\<br />=\frac{n(n+1)}{2}\sum_{i=1}^{n}i=\left[\frac{n(n+1)}{2}\right]^2=<br />\sum_{i=1}^{n}i^3$\\<br />tomando $n=2006$ obtenemos una representacion de $S_{2006}$ en la forma pedida, con exponente 3.](./tex/101095.gif)
![TEX: <br />\begin{align*}<br /> & \text{sumando y restando 1 obtenemos:} \\ <br /> & =\sum\limits_{k=0}^{n}{k![(k+1)-1]} \\ <br /> & =\sum\limits_{k=0}^{n}{[k!}\cdot (k+1)]-k! \\ <br /> & =\sum\limits_{k=0}^{n}{(k+1)!-k!} \\ <br /> & \text{aplicando la propiedad telesc }\!\!\acute{\mathrm{o}}\!\!\text{ pica:} \\ <br /> & \text{=(n+1)!-0!=(n+1)!-1} \\ <br />\end{align*}<br />](./tex/103ffa7f10b193c1d69ce6dd54d68de9.png)
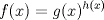 -->
-->