|
|
|
|
|
|
|
  |
 May 31 2006, 01:02 AM May 31 2006, 01:02 AM
Publicado:
#1
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Bueno, me decidi y dado que a mi me encantan las sumatorias, entonces decidi crear un post donde vayamos recolectando problemitas del estilo.
La idea es poner el problema, y ojala aca en el mismo post alguien postee la solucion, o bien el mismo autor, si asi lo desea. De esta forma podremos recopilar un numero importantes de problemas resueltos y crear una Guia de Sumatorias por Fmat, creada con el aporte de cada uno de ustedes. Para darle partida a esta iniciativa, yo pondre el primer problemita, bastante facilito por cierto 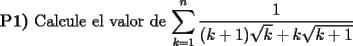 Solucion: -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 May 31 2006, 10:03 AM May 31 2006, 10:03 AM
Publicado:
#2
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 167 Registrado: 17-May 05 Desde: Santiago, Chile Miembro Nº: 38 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Bueno, voy a aportar con un granito de arena a la super guia de sumatorias Fmat
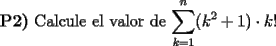 Solucion: Bueno, ojala se entienda la solucion, salu2 ^^ --------------------  |
|
|
|
 May 31 2006, 04:21 PM May 31 2006, 04:21 PM
Publicado:
#3
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 167 Registrado: 17-May 05 Desde: Santiago, Chile Miembro Nº: 38 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Ya, ahora otro:
P3) Calcule el valor de: 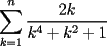 Solucion Listo, que se entienda, salu2 ^^ --------------------  |
|
|
|
 Jun 6 2006, 02:36 PM Jun 6 2006, 02:36 PM
Publicado:
#4
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Veamos...
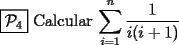 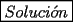 Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Jun 6 2006, 04:56 PM Jun 6 2006, 04:56 PM
Publicado:
#5
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 228 Registrado: 8-August 05 Desde: Santiago de Chile Miembro Nº: 194 |
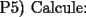 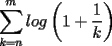 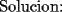 |
|
|
|
 Jun 18 2006, 11:58 PM Jun 18 2006, 11:58 PM
Publicado:
#6
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
CITA 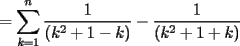 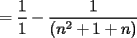 No estaria mal que explicaras un poco mas este paso, que me parece clave dentro de tu desarrollo... Se agradece el buen aporte Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jun 18 2006, 11:59 PM Jun 18 2006, 11:59 PM
Publicado:
#7
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
CITA(Killua @ Jun 6 2006, 03:36 PM) Otro bonito aporte que nunca esta de mas en el hogar... Saludos y Gracias -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jun 19 2006, 12:06 AM Jun 19 2006, 12:06 AM
Publicado:
#8
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
CITA(tt14123 @ Jun 6 2006, 05:56 PM) Muy bonito aporte...vamos formando asi ya una bonita coleccion Mi consejo es cuando quieras poner parentesis mas adecuados a las expresiones uses $\left( 1+\dfrac{1}{k} \right)$ que te deja la expresion como: 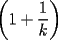 en vez de $(1+\dfrac{1}{k})$ que te genera: 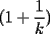 Mi otro consejo es que no veas la suma telescopica solo a partir de 1 hasta n, o a partir de 0. La regla general es la siguiente: Cuando tengas 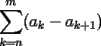 siempre tendras un termino adelantado ( siempre tendras un termino adelantado (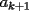 ) y uno atrasado ( ) y uno atrasado (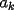 ), luego el valor superior de k ( ), luego el valor superior de k (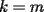 ) debe reemplazarse en el adelantado, y el valor inferior de k ( ) debe reemplazarse en el adelantado, y el valor inferior de k (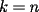 ) debe reemplazarse en el atrasado. ) debe reemplazarse en el atrasado.Asi 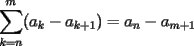 Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jun 19 2006, 12:12 AM Jun 19 2006, 12:12 AM
Publicado:
#9
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Y no puedo evitar unirme a la cruzada con otra sumatoria...a mi juicio dificil a primera vista, y que ruego no ver la solucion hasta haberse dado el gusto de poder intentarla hacer por sus propios meritos
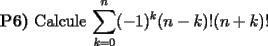 Solucion: -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jun 25 2006, 11:09 AM Jun 25 2006, 11:09 AM
Publicado:
#10
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 167 Registrado: 17-May 05 Desde: Santiago, Chile Miembro Nº: 38 Nacionalidad:  Colegio/Liceo:  Sexo:  |
CITA(Kenshin @ Jun 19 2006, 12:58 AM) No estaria mal que explicaras un poco mas este paso, que me parece clave dentro de tu desarrollo... Se agradece el buen aporte Saludos Yap haer, lo que pasa, es que para formar la telescopica, hay que tener un adelantado y un atrasado como decias mas arriba, luego en la parte antes de la telescopica 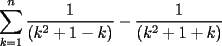 ahora bien, nos gustaria que 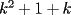 Fuera Igual a Fuera Igual a 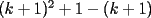 para asi formar la Telescopica, pero si lo trabajamos nos damos cuenta que: para asi formar la Telescopica, pero si lo trabajamos nos damos cuenta que: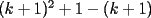 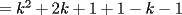 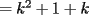 Y luego Todo como antes salu2 --------------------  |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 04:50 PM |






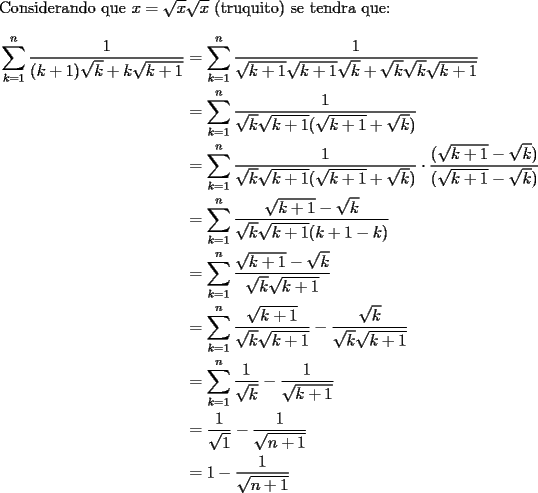





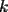 en el parentesis:
en el parentesis: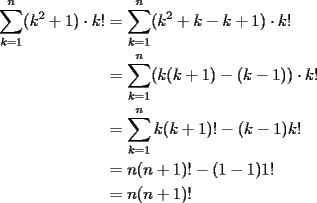
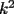
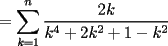
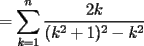
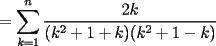
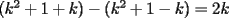
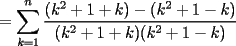
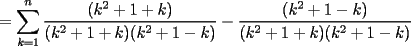
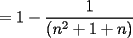


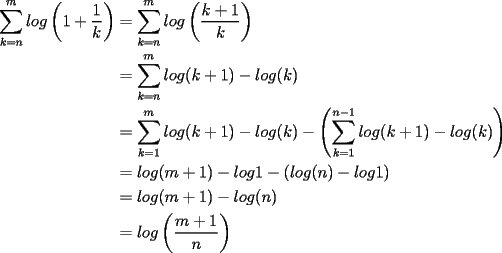
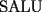

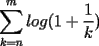
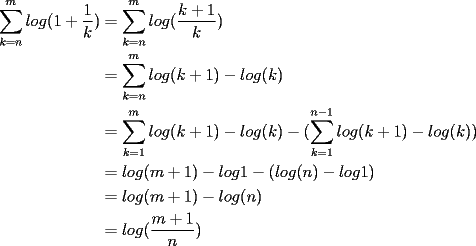
![TEX: \noindent Procedo entonces a entregar la solucion a este encantador problemita:<br />\begin{gather*}<br />\sum_{k=0}^{n}(-1)^k(n-k)!(n+k)!\\<br />=\sum_{k=0}^{n}\frac{1}{2n+2}(-1)^k(n-k)!(n+k)!(2n+2)\\<br />=\frac{1}{2n+2}\sum_{k=0}^{n}(-1)^k(n-k)!(n+k)!((n+k+1)+(n-k+1))\\<br />=\frac{1}{2n+2}\sum_{k=0}^{n}\left[(-1)^k(n-k)!(n+k)!(n+k+1)+(-1)^k(n-k)!(n+k)!(n-k+1)\right]\\<br />=\frac{1}{2n+2}\sum_{k=0}^{n}\left[(-1)^k(n-k)!(n+k+1)!+(-1)^k(n-k+1)!(n+k)!\right]\\<br />=\frac{1}{2n+2}\sum_{k=0}^{n}\left[(-1)^k(n-k)!(n+k+1)!-(-1)^{k-1}(n-(k-1))!(n+(k-1)+1)!\right]\\<br />=\frac{1}{2n+2}\left[(-1)^n(n-n)!(n+n+1)!-(-1)^{0-1}(n-(0-1))!(n+(0-1)+1)!\right]\\<br />=\frac{1}{2n+2}\left[(-1)^n(2n+1)!+(n+1)!n!\right]<br />\end{gather*}](./tex/81370.gif)