|
|
|
|
|
|
|
  |
 May 29 2006, 03:03 PM May 29 2006, 03:03 PM
Publicado:
#1
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
10ª OLIMPIADA DE MAYO Segundo Nivel Problema 1: Julián escribe cinco números enteros positivos, no necesariamente distintos, tales que su producto sea igual a su suma. ¿Cuáles pueden ser los números que escribe Julián? Problema 2: La mamá de Pepito quiere preparar  paquetes de paquetes de  caramelos para regalar en la fiesta de cumpleños, y para ello comprará caramelos surtidos de caramelos para regalar en la fiesta de cumpleños, y para ello comprará caramelos surtidos de  sabores distintos. Puede comprar cualquier número de caramelos pero no puede elegir cuántos son de cada gusto. Ella quiere poner en cada paquete un caramelo de cada sabor, y si esto no es posible usará sólo caramelos de un sabor y todos los paquetes tendrán sabores distintos. Puede comprar cualquier número de caramelos pero no puede elegir cuántos son de cada gusto. Ella quiere poner en cada paquete un caramelo de cada sabor, y si esto no es posible usará sólo caramelos de un sabor y todos los paquetes tendrán  caramelos de ese sabor. Determine el menor número de caramelos que debe comprar para poder armar los caramelos de ese sabor. Determine el menor número de caramelos que debe comprar para poder armar los  paquetes. Explique por qué si compra menos caramelos no tiene la certeza de poder armar los paquetes como quiere. paquetes. Explique por qué si compra menos caramelos no tiene la certeza de poder armar los paquetes como quiere.Problema 3: Disponemos de una mesa de billar de  metros de largo y metros de largo y  metros de ancho, con una única bola en su centro. La lanzamos en línea recta y, tras recorrer metros de ancho, con una única bola en su centro. La lanzamos en línea recta y, tras recorrer 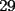 metros, se detiene en una esquina de la mesa. ¿Cuántas veces ha rebotado la bola contra los bordes de la mesa? metros, se detiene en una esquina de la mesa. ¿Cuántas veces ha rebotado la bola contra los bordes de la mesa?Nota: Cuando la bola rebota contra un borde de la mesa los dos ángulos que forma su trayectoria con el borde de la mesa son iguales. Problema 4: Encuentre todos los números naturales 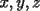 que verifican simultáneamente que verifican simultáneamente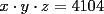 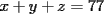 Problema 5: Sobre un tablero de 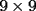 , dividido en casillas de , dividido en casillas de 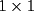 , se colocan, sin superposiciones y sin sobresalirse del tablero, piezas de la forma , se colocan, sin superposiciones y sin sobresalirse del tablero, piezas de la forma Cada pieza cubre exactamente  casillas. casillas.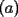 A partir del tablero vacío, ¿cuál es la máxima cantidad de piezas que se pueden colocar? A partir del tablero vacío, ¿cuál es la máxima cantidad de piezas que se pueden colocar?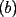 A partir del tablero con A partir del tablero con  piezas ya colocadas como muestra el diagrama siguiente, piezas ya colocadas como muestra el diagrama siguiente, ¿cuál es la máxima cantidad de piezas que se pueden colocar? Resumen de soluciones -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Jul 4 2006, 05:08 PM Jul 4 2006, 05:08 PM
Publicado:
#2
|
|
 Máquina que convierte café en teoremas Grupo: Colaborador Silver Mensajes: 1.665 Registrado: 18-August 05 Desde: Concepción Miembro Nº: 247 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
P1
los numeors pueden ser 1 1 1 2 5 1*1*1*2*5=10 1+1+1+2+5=10 --------------------  Manual para subir imágenes y archivos a fmat (con servidor propio) Manual de latex Estilo Propio Lista de libros en fmat    "Un Matemático es una máquina que trasforma café en teoremas"(Erdös) --- Consultas, sugerencias, reclamos via mp o a los correos mencionados. |
|
|
|
 Aug 20 2006, 03:52 PM Aug 20 2006, 03:52 PM
Publicado:
#3
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
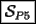 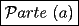   screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img222.imageshack.us/img222/9068/tableritonl5.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img222.imageshack.us/img222/9068/tableritonl5.png');}" />  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img403.imageshack.us/img403/8538/tablero2uq4.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img403.imageshack.us/img403/8538/tablero2uq4.png');}" />    screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img20.imageshack.us/img20/5127/tablerooriginalis5.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img20.imageshack.us/img20/5127/tablerooriginalis5.png');}" />Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Oct 14 2006, 02:22 PM Oct 14 2006, 02:22 PM
Publicado:
#4
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 374 Registrado: 16-September 06 Desde: New Haven, CT, USA. Miembro Nº: 2.275 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Pregunta 1:
Los numeros pueden ser: 1,1,2,2,2. 1*1*2*2*2 = 1+1+2+2+2. |
|
|
|
 Oct 14 2006, 05:16 PM Oct 14 2006, 05:16 PM
Publicado:
#5
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
CITA(The Lord @ Oct 14 2006, 03:22 PM) La gracia de estos problemas es que pongas alguna justificación, y que des todas las posibilidades. Así que a esperar un resultado más contundente, porque probando dudo que en una prueba como esta ganes algo de puntaje. La solución es correcta, pero hay que mostrar todas las posibilidades, y si no hay, decir por qué. A seguir intentando CITA(zirou @ Jul 4 2006, 06:08 PM) Lo mismo para zirou... ahí pueden ver que hay más de una solución. Saludos Mensaje modificado por Killua el Oct 14 2006, 05:19 PM -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Dec 4 2006, 01:19 PM Dec 4 2006, 01:19 PM
Publicado:
#6
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 374 Registrado: 16-September 06 Desde: New Haven, CT, USA. Miembro Nº: 2.275 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
CITA(Killua @ May 29 2006, 04:03 PM)  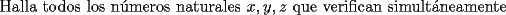 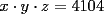 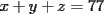 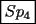    Mensaje modificado por The Lord el Dec 4 2006, 01:28 PM |
|
|
|
 Dec 27 2006, 01:37 AM Dec 27 2006, 01:37 AM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
CITA(Killua @ Aug 20 2006, 04:52 PM) 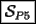 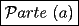   screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img222.imageshack.us/img222/9068/tableritonl5.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img222.imageshack.us/img222/9068/tableritonl5.png');}" />  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img403.imageshack.us/img403/8538/tablero2uq4.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img403.imageshack.us/img403/8538/tablero2uq4.png');}" />    screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img20.imageshack.us/img20/5127/tablerooriginalis5.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img20.imageshack.us/img20/5127/tablerooriginalis5.png');}" />Saludos Creo que fallaste en la parte (a); ya que afirmas que no se pueden colocar mas de 25 fichas; si embargo en la parte (b) pones un diagrama donde caben 26 Saludos |
|
|
|
 Jan 8 2007, 10:01 PM Jan 8 2007, 10:01 PM
Publicado:
#8
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 2 Registrado: 4-January 07 Miembro Nº: 3.514 Sexo:  |
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 08:55 PM |












