|
|
|
|
|
|
|
  |
 May 28 2006, 06:51 PM May 28 2006, 06:51 PM
Publicado:
#1
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
8ª OLIMPIADA DE MAYO Segundo Nivel Problema 1: Utilizando cubitos blancos de lado 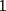 se armó un prisma (sin huecos). Se pintaron de negro las caras del prisma. Se sabe que los cubitos que quedaron con exactamente se armó un prisma (sin huecos). Se pintaron de negro las caras del prisma. Se sabe que los cubitos que quedaron con exactamente 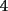 caras blancas son caras blancas son 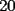 en total. Determina cuáles pueden ser las dimensiones del prisma. Da todas las posibilidades. en total. Determina cuáles pueden ser las dimensiones del prisma. Da todas las posibilidades.Problema 2: Sea 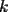 un número entero positivo fijo, un número entero positivo fijo, 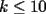 . Dada una lista de diez números, la operación permitida es: elegir . Dada una lista de diez números, la operación permitida es: elegir 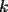 números de la lista, y sumarle números de la lista, y sumarle 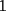 a cada uno de ellos. Se obtiene así una nueva lista de diez números. Si inicialmente se tiene la lista a cada uno de ellos. Se obtiene así una nueva lista de diez números. Si inicialmente se tiene la lista 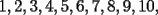 determine los valores de determine los valores de 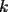 para los que es posible, mediante una secuencia de operaciones permitidas, obtener una lista que tenga los diez números iguales. para los que es posible, mediante una secuencia de operaciones permitidas, obtener una lista que tenga los diez números iguales.En cada caso indica la secuencia. Problema 3: En un 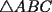 , rectángulo en , rectángulo en 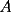 e isósceles, sea e isósceles, sea 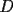 un punto del lado un punto del lado 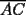 , distinto de , distinto de 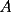 y y 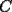 y sea y sea 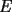 el punto de la prolongación del lado el punto de la prolongación del lado 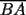 tal que el tal que el 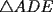 es isósceles. Si es isósceles. Si 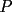 es el punto medio de es el punto medio de 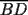 , , 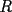 es el punto medio de es el punto medio de 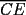 y y 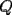 el punto en donde se cortan el punto en donde se cortan 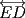 y y 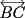 , pruebe que el cuadrilátero , pruebe que el cuadrilátero 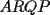 es un cuadrado. es un cuadrado.Problema 4: Los vértices de un polígono regular de 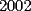 lados están numerados del lados están numerados del 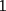 al al 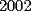 , en sentido horario. Dado un entero , en sentido horario. Dado un entero 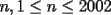 , se colorea de azul el vértice , se colorea de azul el vértice  , luego, siguiendo el sentido horario, se cuentan , luego, siguiendo el sentido horario, se cuentan  vértices comenzando en el siguiente de vértices comenzando en el siguiente de  , y se colorea de azul el número , y se colorea de azul el número  . Y así sucesivamente, a partir del vértice que sigue al último vértice que se ha coloreado, se cuentan . Y así sucesivamente, a partir del vértice que sigue al último vértice que se ha coloreado, se cuentan  vértices, coloreados o sin colorear, y al número vértices, coloreados o sin colorear, y al número  se lo colorea de azul. Cuando el vértice que toca colorear ya es azul, el proceso se detiene. Denotamos se lo colorea de azul. Cuando el vértice que toca colorear ya es azul, el proceso se detiene. Denotamos 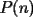 al conjunto de vértices azules que se obtienen con este procedimiento cuando se comienza por el vértice al conjunto de vértices azules que se obtienen con este procedimiento cuando se comienza por el vértice  . Por ejemplo, . Por ejemplo, 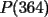 está formado por los vértices está formado por los vértices 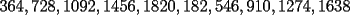 y y 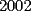 Determine todos los enteros 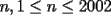 , tales que , tales que 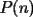 tiene exactamente tiene exactamente 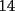 vértices. vértices.Problema 5: Dados  e e 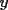 enteros positivos, consideramos una cuadrícula de enteros positivos, consideramos una cuadrícula de 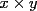 , que tiene coloreados de rojo los , que tiene coloreados de rojo los 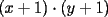 puntos que son vértices de cuadraditos. Inicialmente hay una hormiga en cada uno de los puntos rojos. En un instante dado, todas las hormigas comienzan a caminar por las líneas de la cuadrícula, y todas lo hacen con la misma velocidad. Cada vez que llegan a un punto rojo, giran puntos que son vértices de cuadraditos. Inicialmente hay una hormiga en cada uno de los puntos rojos. En un instante dado, todas las hormigas comienzan a caminar por las líneas de la cuadrícula, y todas lo hacen con la misma velocidad. Cada vez que llegan a un punto rojo, giran 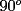 en alguna dirección. en alguna dirección.Determine todos los valores de  e e 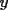 para los cuales es posible que las hormigas continúen moviéndose indefinidamente de manera que en ningún momento haya dos o más hormigas en un mismo punto rojo. (No interesan las posibles coincidencias en puntos de las líneas de la cuadríicula que no son rojos) para los cuales es posible que las hormigas continúen moviéndose indefinidamente de manera que en ningún momento haya dos o más hormigas en un mismo punto rojo. (No interesan las posibles coincidencias en puntos de las líneas de la cuadríicula que no son rojos)Resumen de soluciones -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Apr 5 2007, 09:13 PM Apr 5 2007, 09:13 PM
Publicado:
#2
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 14 Registrado: 16-October 06 Miembro Nº: 2.547 Nacionalidad:  Sexo:  |
En el primer problema del prisma que se pintaba negro, me dio que los valores deben satisfacer la ecuación:
a+b+c=11 Los valores que cumplen con la condicion y con el problema inicial son 4,4,3 quisiera saber si esta bien o no. Mensaje modificado por Alfonso el Apr 6 2007, 02:04 PM |
|
|
|
 Apr 6 2007, 05:41 PM Apr 6 2007, 05:41 PM
Publicado:
#3
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 14 Registrado: 16-October 06 Miembro Nº: 2.547 Nacionalidad:  Sexo:  |
Tambien 3,3,5
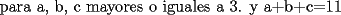
|
|
|
|
 Mar 20 2013, 10:50 PM Mar 20 2013, 10:50 PM
Publicado:
#4
|
|
 Doctor en Matemáticas Grupo: Colaborador Silver Mensajes: 193 Registrado: 17-August 12 Desde: Loncuma :3 Miembro Nº: 110.077 Nacionalidad:  Sexo:  |
Solucion p3:
Denotemos 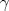 al al 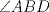 y y 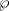 al al 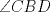 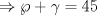 . Tenemos que . Tenemos que 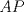 es mediana del es mediana del 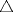 rectangulo rectangulo 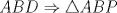 es isosceles de base es isosceles de base 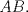 Tenemos que el 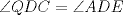 (opuestos por el vertice) (opuestos por el vertice) 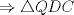 es rectangulo en es rectangulo en 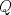 e isosceles e isosceles 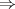 el cuadrilatero el cuadrilatero 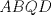 es ciclico de esto es ciclico de esto 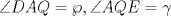 . .Como 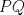 es mediana del es mediana del 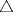 rectangulo rectangulo 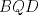 el el 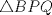 es isosceles de base es isosceles de base 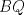 , , 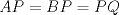 . .Por propiedad "pac-man" 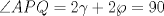 entonces entonces 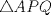 es rectangulo en es rectangulo en 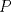 e isosceles. e isosceles.Tenemos que el cuadrialtero 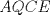 es ciclico ya que, es ciclico ya que, 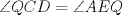 y y 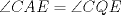 (corbata) (corbata) 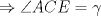 y y 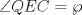 . Como . Como 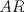 y y 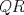 son respectivas medianas de los triangulos rectangulos son respectivas medianas de los triangulos rectangulos 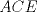 y y 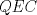 , ,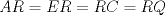 . .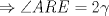 y y 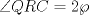 . Tenemos que los . Tenemos que los 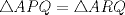 de esto, de esto, 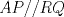 y y 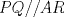 Por lo tanto el cuadrilatero 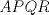 es un cuadrado. es un cuadrado.
Mensaje modificado por Niklaash el Mar 20 2013, 11:02 PM |
|
|
|
 Mar 22 2013, 03:21 PM Mar 22 2013, 03:21 PM
Publicado:
#5
|
|
|
Dios Matemático Grupo: Colaborador Silver Mensajes: 423 Registrado: 4-January 11 Miembro Nº: 82.624 Nacionalidad:  Universidad: .png) Sexo:  |
Hola Niklaash que bueno que te estés interesando en el sector olimpiadas, hace falta gente nueva que se integre por estos lados
Tu solución al problema esta super buena en general pero tiene unos detalles que se pueden mejorar, por ejemplo cuando mencionas que los triángulos APQ y ARQ son congruentes tienes que mencionar el criterio de congruencia que ocupas, (esto es más que nada por un tema de formalidad y también para que quien revise pueda entender que concluiste la congruencia a través de argumentos validos y no chamullaste) Por otro lado al final dices de esto, 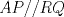 y y 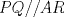 Por lo tanto el cuadrilatero 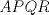 es un cuadrado. es un cuadrado.Pero, ¿es cierto que AP//RQ y PQ//AR es suficiente para concluir que APQR es un cuadrado? esa parte de la solución habría que volver a formularla. Se que son detalles pequeños pero tienes que considerar que al momento de competir en una olimpiada detalles como esos te puede perjudicar, así que es mejor que te acostumbres a dar soluciones intachables Como dato curioso la circunferencia circunscrita al triangulo APQR sería la circunferencia de los nueve puntos del triangulo EBC |
|
|
|
 Mar 22 2013, 06:12 PM Mar 22 2013, 06:12 PM
Publicado:
#6
|
|
 Doctor en Matemáticas Grupo: Colaborador Silver Mensajes: 193 Registrado: 17-August 12 Desde: Loncuma :3 Miembro Nº: 110.077 Nacionalidad:  Sexo:  |
Hola Niklaash que bueno que te estés interesando en el sector olimpiadas, hace falta gente nueva que se integre por estos lados Tu solución al problema esta super buena en general pero tiene unos detalles que se pueden mejorar, por ejemplo cuando mencionas que los triángulos APQ y ARQ son congruentes tienes que mencionar el criterio de congruencia que ocupas, (esto es más que nada por un tema de formalidad y también para que quien revise pueda entender que concluiste la congruencia a través de argumentos validos y no chamullaste) Por otro lado al final dices Pero, ¿es cierto que AP//RQ y PQ//AR es suficiente para concluir que APQR es un cuadrado? esa parte de la solución habría que volver a formularla. Se que son detalles pequeños pero tienes que considerar que al momento de competir en una olimpiada detalles como esos te puede perjudicar, así que es mejor que te acostumbres a dar soluciones intachables Como dato curioso la circunferencia circunscrita al triangulo APQR sería la circunferencia de los nueve puntos del triangulo EBC Oh... se me fue señalar el criterio que use para validar la congruencia de los triangulos u,u Pero... al señalar que los triangulos que "formaban" el cuadrado son congruentes tenemos que los 4 lados que formaban al cuadrado eran iguales, y por el paralelismo formamos la "Z" (diagonal) y tenemos congruencia de angulos, y angulos rectos de los triangulos :c , nose si hay que justificar mas cosas :c pd: Gracias por la recibida <3 |
|
|
|
 Mar 22 2013, 06:14 PM Mar 22 2013, 06:14 PM
Publicado:
#7
|
|
 Doctor en Matemáticas Grupo: Colaborador Silver Mensajes: 193 Registrado: 17-August 12 Desde: Loncuma :3 Miembro Nº: 110.077 Nacionalidad:  Sexo:  |
Hola Niklaash que bueno que te estés interesando en el sector olimpiadas, hace falta gente nueva que se integre por estos lados Tu solución al problema esta super buena en general pero tiene unos detalles que se pueden mejorar, por ejemplo cuando mencionas que los triángulos APQ y ARQ son congruentes tienes que mencionar el criterio de congruencia que ocupas, (esto es más que nada por un tema de formalidad y también para que quien revise pueda entender que concluiste la congruencia a través de argumentos validos y no chamullaste) Por otro lado al final dices Pero, ¿es cierto que AP//RQ y PQ//AR es suficiente para concluir que APQR es un cuadrado? esa parte de la solución habría que volver a formularla. Se que son detalles pequeños pero tienes que considerar que al momento de competir en una olimpiada detalles como esos te puede perjudicar, así que es mejor que te acostumbres a dar soluciones intachables Como dato curioso la circunferencia circunscrita al triangulo APQR sería la circunferencia de los nueve puntos del triangulo EBC Oh... se me fue señalar el criterio que use para validar la congruencia de los triangulos u,u Pero... al señalar que los triangulos que "formaban" el cuadrado son congruentes tenemos que los 4 lados que formaban al cuadrado eran iguales, y por el paralelismo formamos la "Z" (diagonal) y tenemos congruencia de angulos, y angulos rectos de los triangulos :c , nose si hay que justificar mas cosas :c pd: Gracias por la recibida <3 |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 08:53 PM |










