|
|
|
|
|
|
|
  |
 Jun 25 2005, 07:58 PM Jun 25 2005, 07:58 PM
Publicado:
#1
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Y bueno,aqui los del Tercer Nivel Individual

-------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jun 26 2005, 08:21 AM Jun 26 2005, 08:21 AM
Publicado:
#2
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 24 Registrado: 14-June 05 Desde: Aquí... Miembro Nº: 106 Nacionalidad:  Sexo:  |
YAAAAAAAAAAAAAAA.....AHORA SIP
 screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img88.echo.cx/img88/6991/paranatalia4uo.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img88.echo.cx/img88/6991/paranatalia4uo.png');}" />Lo primero que hice fue trazar la altura del triángulo, La cual llamé 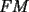 . Esta altura mide . Esta altura mide 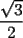 ; ya que la altura de un triángulo equilátero corta a la base en su punto medio, y se usa Pitágoras para determinarlo. ; ya que la altura de un triángulo equilátero corta a la base en su punto medio, y se usa Pitágoras para determinarlo.Después se traza una paralela a 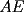 desde el punto desde el punto 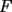 y corta al lado del cuadrado en el punto y corta al lado del cuadrado en el punto 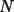 , este segmento , este segmento 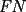 , mide , mide 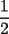 , igual que , igual que 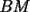 . .Ahora tenemos que los triángulos 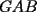 y y 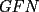 , son semejantes, por criterio AA, ya que poseen cada uno un ángulo de , son semejantes, por criterio AA, ya que poseen cada uno un ángulo de 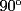 y los ángulos y los ángulos 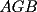 Y Y 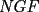 son iguales, por ser contrarios por el vértice. son iguales, por ser contrarios por el vértice.Si son semejantes quiere decir que sus lados poseen cierta proporcionalidad, y es así como llegamos a que 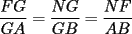 Y podemos reemplazar sabiendo que 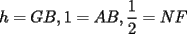 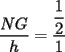 DE LO CUAL OBTENEMOS QUE 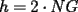 y sabiendo que 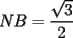 (al igual que la altura del triángulo), y que (al igual que la altura del triángulo), y que 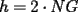 , tenemos que , tenemos que 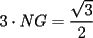 De lo cual obtenemos que De lo cual obtenemos que 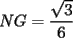 Y REEMPLAZANDO ESA MEDIDA EN 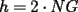 , TENEMOS QUE , TENEMOS QUE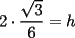 Y Y 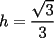 ahora conociendo la medida de 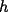 , podemos sacar la medida de las áreas de , podemos sacar la medida de las áreas de 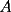 Y Y 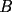 : :el área de 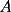 : :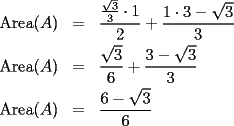 el área de 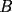 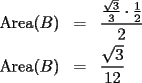 --------------------  |
|
|
|
 Jun 26 2005, 08:46 AM Jun 26 2005, 08:46 AM
Publicado:
#3
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 24 Registrado: 14-June 05 Desde: Aquí... Miembro Nº: 106 Nacionalidad:  Sexo:  |
APZ Y SE ME OLVIDó DECIR QUE PARA SACAR EL ÁREA DE
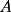 TRACÉ UNA PARALELA AL LADO 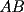 DEL CUADRADO Y CALCULÉ EL AREA POR SEPARADO DEL TRIÁNGULO DEL CUADRADO Y CALCULÉ EL AREA POR SEPARADO DEL TRIÁNGULO 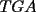 Y DEL RECTÁNGULO Y DEL RECTÁNGULO 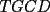  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img230.echo.cx/img230/2421/uyuy4my.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img230.echo.cx/img230/2421/uyuy4my.png');}" />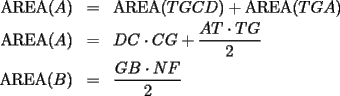 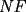 (altura del triángulo de área (altura del triángulo de área 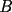 ) )y esop....así obtube las áreas 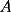 Y Y 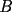 ......... :wink: :wink: :wink: :wink: ......... :wink: :wink: :wink: :wink:
--------------------  |
|
|
|
 Jun 26 2005, 09:08 AM Jun 26 2005, 09:08 AM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
La solución está muy buena pero quiero comentar un pequeño detalle:
Cuando dices que los triángulos 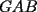 y y 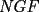 son semejantes, se supone que los vértices homólogos se escriben en el mismo orden relativo En un español menos técnico, quiero decir que si el ángulo en son semejantes, se supone que los vértices homólogos se escriben en el mismo orden relativo En un español menos técnico, quiero decir que si el ángulo en 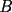 es recto, así como el ángulo en es recto, así como el ángulo en 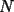 , entonces ambos deberían ocupar el mismo orden relativo al escribir los vértices. Si respetamos esto, entonces la semejanza sería , entonces ambos deberían ocupar el mismo orden relativo al escribir los vértices. Si respetamos esto, entonces la semejanza sería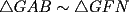 Cuando uno respeta el orden relativo, tiene la ventaja que se entienden de inmediato las relaciones: 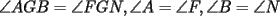 , y también que , y también que 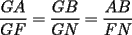 , o sea es rápido sacar toda la información de la semejanza. , o sea es rápido sacar toda la información de la semejanza.O sea, es más que una simple norma de simplicidad, que facilita la lectura (dijiste que los triángulos son semejantes, está bien, nunca pusiste " 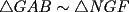 ") ")Esperamos la solución para el problema 2 -------------------- |
|
|
|
 Jun 26 2005, 10:11 AM Jun 26 2005, 10:11 AM
Publicado:
#5
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 24 Registrado: 14-June 05 Desde: Aquí... Miembro Nº: 106 Nacionalidad:  Sexo:  |
ya listo, lo arregle, la verdad es que de repente se me van esos detalles, pero prometo poner más cuidado para la próxima, muchas gracias por decirmelo......
--------------------  |
|
|
|
 Jun 27 2005, 06:31 PM Jun 27 2005, 06:31 PM
Publicado:
#6
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 365 Registrado: 27-May 05 Desde: Puente Asalto, Santiago Miembro Nº: 68 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Nosé si es algún aporte, pero yo solucioné el enunciado 1 de una manera un poquito diferente a Natita (sólo en un detalle, y al final llegamos a los mismos resultados).
Guiémonos por el dibujito de Naty ^^ También tracé la altura del triángulo 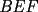 (llamada (llamada 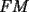 ), porque con eso se solucionaba todo jejeje. Bueno, luego que se calculaba con Pitágoras y todo la medida de ), porque con eso se solucionaba todo jejeje. Bueno, luego que se calculaba con Pitágoras y todo la medida de 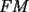 , Yo me di cuenta de que se podía establecer Thales con los triángulos , Yo me di cuenta de que se podía establecer Thales con los triángulos 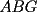 y y 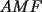 (son semejantes por el ángulo recto que poseen y porque el (son semejantes por el ángulo recto que poseen y porque el 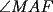 es común para ambos; Criterio AA), por lo que hice la siguiente proporción: es común para ambos; Criterio AA), por lo que hice la siguiente proporción: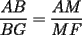 Reemplazamos los datos 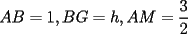 y y 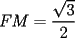 : :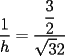 Multiplicamos, dividimos, etc etc 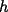 que es lo mismo que le dió a Natita, que es lo mismo que le dió a Natita, 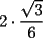 . .Después calculé el área del triángulo 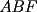 , pues su base es , pues su base es 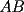 y su altura y su altura 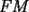 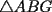 , y con estos datos establecí que , y con estos datos establecí que 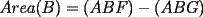 Y me dio lo mismo:P De la misma manera, calculé además el área del cuadrado 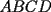 , y luego , y luego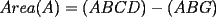 Y también da el mismo valor de Natita __ Bueno eso ^^ .. sólo quería mencionar que yo lo calculé así, espero que no esté malo ___ --------------------  |
|
|
|
 Jun 27 2005, 06:38 PM Jun 27 2005, 06:38 PM
Publicado:
#7
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 24 Registrado: 14-June 05 Desde: Aquí... Miembro Nº: 106 Nacionalidad:  Sexo:  |
hulas!!!!
pily creo que no.........estás mal...mas encima plagiaste mi dibujito......noooooo...asi no se vale........ ohhhhhh bueno amiga....me alegro que hayas puesto tu solución.....aunque te daba lata...jajaja.....espero que sigas así y podamos ayudarnos mucho más y así continuar aprendiendo....adiosin...suerte....sigue asi --------------------  |
|
|
|
 Jul 2 2005, 11:41 PM Jul 2 2005, 11:41 PM
Publicado:
#8
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 414 Registrado: 19-May 05 Desde: puente alto, santiago Miembro Nº: 45 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
La solucion al problema dos es la siguiente:
tenemos seis puntos donde no hay tres colineales. nuestra intencion sera ponernos siempre en el peor de los casos y llegar a la conclusion que incluso siendo pesimistas, siempre habra un triangulo formado por segmentos del mismo color. Tomemos un punto A, cualquiera de los 6. De ese punto saldran 5 segmentos, notemos que cualquiera sea la forma de colorear estos segmentos, siempre podremos afirmar que hay al menos tres que tienen el mismo color ( es imposible que haan a lo mas 2 rojos y a lo mas 2 azules). Supongamos que estos segmentos( los que poseen al menos tres de l mismo color) son azules, sin perdida de generalidad. AB, AC y AD son estos segmetos azules ( como se ve en la figura).  Ahora debemos colorear los segementos BC, BD y CD. 1) para el segmento BC, tenemos dos opciones si es azul el problema esta resuelto porque tendremos que el triangulo ABC es azul, como queremos ser pesimistas, no queremos que esto suceda entonces BC es rojo. 2) para el segmento CD sucede lo mismo, y por razonamiento analogo concluimos que es rojo.  3) ahora para el segmento BD tenemos dos opciones: a) si es azul, entonces tendremos que el triangulo ABD es azul. B) si es rojo tendremos que el triangulo BCD es rojo. entonces hemos llegado que cualquiera sea el camino, y por mas que no queramos se nos formara un triangulo del mismo color. -------------------- "No tenemos la solucion a todos los problemas del mundo en nuestras manos... Pero frente a los problemas del mundo tenemos nuestras manos..."
Teresa de Calcuta |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 18th October 2025 - 08:15 PM |









