Prueba Grupal (Tercer y Cuarto Nivel) - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > Campeonato Interescolar > Campeonato Interescolar 2006 > Segunda Fecha

3 Páginas:

1 2 3 >

Reply to this topic

Start new topic

Prueba Grupal (Tercer y Cuarto Nivel)

Zirou Ver Perfil del Miembro Ver los mensajes de este miembro	May 20 2006, 09:04 PM Publicado: #1
Máquina que convierte café en teoremas Grupo: Colaborador Silver Mensajes: 1.665 Registrado: 18-August 05 Desde: Concepción Miembro Nº: 247 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	aca esta Archivo(s) Adjunto(s) grupal_cemat_20001.jpg ( 182.06k ) Número de descargas: 11 -------------------- $TEX: $mathcal{Z}$ $imath$ $Re$ $varnothing$ $mho$$ Manual para subir imágenes y archivos a fmat (con servidor propio) Manual de latex Estilo Propio Lista de libros en fmat "Un Matemático es una máquina que trasforma café en teoremas"(Erdös) --- Consultas, sugerencias, reclamos via mp o a los correos mencionados.

Guía Rojo Ver Perfil del Miembro Ver los mensajes de este miembro	May 20 2006, 10:19 PM Publicado: #2
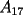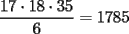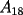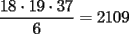Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 903 Registrado: 28-May 05 Desde: Santiago, Chile Miembro Nº: 69 Nacionalidad: Colegio/Liceo: Sexo:	el 1... es cosa de acotarlo... el término inferior derecho (el mayor) de $TEX: $A_{17}$$ es igual a: $TEX: $\dfrac{17\cdot 18\cdot 35}{6}=1785$$ procediendo de igual forma con $TEX: $A_{18}$$ tenemos: $TEX: $\dfrac{18\cdot 19\cdot 37}{6}=2109$$ luego, todos los números que cumplan: 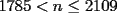$TEX: $1785<n\le 2109$$ están en 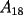$TEX: $A_{18}$$ 2006 cumple, por lo que la deducción es obvia... -------------------- Bachiller en Ciencias (ex) Estudiante de Medicina Estudiante de Ingeniería Civil de Industrias, diploma en Ingeniería Matemática Pontificia Universidad Católica de Chile "El espíritu del matemático busca la belleza del pensamiento, y esa va de la mano con la filosofía." - Héctor Hardy Pastén Vásquez "¿Qué te hace pensar que si tienes dos elementos de un conjunto con otros dos elementos de otro conjunto se origina uno nuevo con cuatro? Es sólo el sentido común, no te imaginas que los elementos aparecen de la nada, pero resulta que con el sólo hecho de cuestionar el sentido común, se podría afirmar que cuando juntas cuatro elementos aparecen miles de elementos más. Y si lo demuestras, todo se basa en la razón." - Alonso Duque Vega, razonador por excelencia $TEX: $S=1+dfrac{1}{2}+dfrac{1}{3}+dfrac{1}{4}+dfrac{1}{5}+ldots$$ Esta serie converge! He encontrado una maravillosa demostración de esto, pero no cabe en la estrechez de esta firma...

Guía Rojo Ver Perfil del Miembro Ver los mensajes de este miembro	May 20 2006, 10:25 PM Publicado: #3
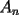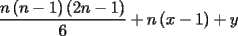Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 903 Registrado: 28-May 05 Desde: Santiago, Chile Miembro Nº: 69 Nacionalidad: Colegio/Liceo: Sexo:	para encontrar un término cualquiera en $TEX: $A_n$$ que se encuentra en la fila x, columna y, tenemos la siguiente fórmula (no es difícil de probar): $TEX: $\dfrac{n\left(n-1\right)\left(2n-1\right)}{6}+n\left(x-1\right)+y$$ el término central de 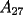$TEX: $A_{27}$$ está en la fila 14, columna 14... 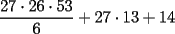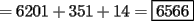luego, éste es: $TEX: $\dfrac{27\cdot 26\cdot 53}{6}+27\cdot 13+14$$ $TEX: $=6201+351+14=\boxed{6566}$$ -------------------- Bachiller en Ciencias (ex) Estudiante de Medicina Estudiante de Ingeniería Civil de Industrias, diploma en Ingeniería Matemática Pontificia Universidad Católica de Chile "El espíritu del matemático busca la belleza del pensamiento, y esa va de la mano con la filosofía." - Héctor Hardy Pastén Vásquez "¿Qué te hace pensar que si tienes dos elementos de un conjunto con otros dos elementos de otro conjunto se origina uno nuevo con cuatro? Es sólo el sentido común, no te imaginas que los elementos aparecen de la nada, pero resulta que con el sólo hecho de cuestionar el sentido común, se podría afirmar que cuando juntas cuatro elementos aparecen miles de elementos más. Y si lo demuestras, todo se basa en la razón." - Alonso Duque Vega, razonador por excelencia $TEX: $S=1+dfrac{1}{2}+dfrac{1}{3}+dfrac{1}{4}+dfrac{1}{5}+ldots$$ Esta serie converge! He encontrado una maravillosa demostración de esto, pero no cabe en la estrechez de esta firma...

GlagosSA Ver Perfil del Miembro Ver los mensajes de este miembro	May 20 2006, 10:36 PM Publicado: #4
Dios Matemático Grupo: Usuario FMAT Mensajes: 380 Registrado: 22-April 06 Desde: Chillan, chile, sudamerica, el mundo Miembro Nº: 912 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	para sacar el termino medio de eso, nosotros sacamos la semisuma del ultimo vertice con el primero. -------------------- Un dia aciago del año 212 a.C., durante la segunda querra punica, Arquimedes se encontraba contemplando algunos circulos que tenia dibujados sobre la arena. Un soldado romano trató de interrumpirlo. La reaccion del genio frente a la presencia del enemigo invasor, el lugar de ser miedo, fue indignacion por verse interrumpido en su trabajo intelectual.-"¡deje en paz a mis circulos!"- Unos minutos mas tarde, el maestro matematico de 75 años, muere atravesado por una espada romana. La altura de tu Vuelo dependera del tamaño de los Ideales que lleves por Alas.. El beso es la distancia mas corta entre Tú y Yo..

Evidal Ver Perfil del Miembro Ver los mensajes de este miembro	May 20 2006, 10:38 PM Publicado: #5
Matemático Grupo: Usuario FMAT Mensajes: 33 Registrado: 7-August 05 Miembro Nº: 178 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	P3: Sabemos que el vertice superior izquierdo corresponde al sucesor del termino inferior derecho del cuadrado anterior, por lo tanto: SI= $TEX: \[<br />\frac{{26 \bullet 27 \bullet 53}}<br />{6} + 1 = 6202<br />\]<br />$ EL termino superior derecho se encuentra 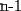$TEX: n-1$ lugares a su derecha, por lo que: SD= SI + 26 = 6228 Luego el termino inferior derecho, es la suma de los cuadrados hasta n ID= $TEX: \[<br />\frac{{27 \bullet 28 \bullet 55}}<br />{6} = 6930<br />\]<br />$ Finalmente el termino inferior izquierdo se ubica 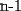$TEX: n-1$ lugares a la izquierda del ultimo termino II= ID - 26 = 6904

Guía Rojo Ver Perfil del Miembro Ver los mensajes de este miembro	May 20 2006, 10:39 PM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 903 Registrado: 28-May 05 Desde: Santiago, Chile Miembro Nº: 69 Nacionalidad: Colegio/Liceo: Sexo:	CITA(GlagosSA @ May 21 2006, 12:36 AM) para sacar el termino medio de eso, nosotros sacamos la semisuma del ultimo vertice con el primero. pues para eso habría que probar algo más difícil, e incluso no sería general como lo que yo dije... además, esta fórmula nos ayudó a varias preguntas más... -------------------- Bachiller en Ciencias (ex) Estudiante de Medicina Estudiante de Ingeniería Civil de Industrias, diploma en Ingeniería Matemática Pontificia Universidad Católica de Chile "El espíritu del matemático busca la belleza del pensamiento, y esa va de la mano con la filosofía." - Héctor Hardy Pastén Vásquez "¿Qué te hace pensar que si tienes dos elementos de un conjunto con otros dos elementos de otro conjunto se origina uno nuevo con cuatro? Es sólo el sentido común, no te imaginas que los elementos aparecen de la nada, pero resulta que con el sólo hecho de cuestionar el sentido común, se podría afirmar que cuando juntas cuatro elementos aparecen miles de elementos más. Y si lo demuestras, todo se basa en la razón." - Alonso Duque Vega, razonador por excelencia $TEX: $S=1+dfrac{1}{2}+dfrac{1}{3}+dfrac{1}{4}+dfrac{1}{5}+ldots$$ Esta serie converge! He encontrado una maravillosa demostración de esto, pero no cabe en la estrechez de esta firma...

fs_tol Ver Perfil del Miembro Ver los mensajes de este miembro	May 20 2006, 10:46 PM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 670 Registrado: 30-January 06 Desde: Ñuñoa, Santiago Miembro Nº: 524 Nacionalidad: Universidad: Sexo:	$TEX: \noindent Para la 4 demostramos que la suma de los terminos k y n-k de la diagonal principal de un cuadrado de orden n es siempre la misma, luego la suma de toda la diagonal es $\frac{(a+b)n}{2}$, donde a y b son el primer y ultimo vertice.<br />$S=177282$$ -------------------- $TEX: $CARITA$$

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	May 20 2006, 10:47 PM Publicado: #8
Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	El aporte de "la semisuma de los extremos = término central" es un truco muy bueno, para resolver toda esta prueba en muy poco tiempo. Así que no debiera mirarse en menos -------------------- Sebastián Elías Puelma Moya Administrador FMAT

Evidal Ver Perfil del Miembro Ver los mensajes de este miembro	May 20 2006, 10:55 PM Publicado: #9
Matemático Grupo: Usuario FMAT Mensajes: 33 Registrado: 7-August 05 Miembro Nº: 178 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(fs_tol @ May 20 2006, 11:46 PM) $TEX: \noindent Para la 4 demostramos que la suma de los terminos k y n-k de la diagonal principal de un cuadrado de orden n es siempre la misma, luego la suma de toda la diagonal es $\frac{(a+b)n}{2}$, donde a y b son el primer y ultimo vertice.<br />$S=177282$$ En mi grupo llegamos al mismo resultado, pero con una formula mas compleja: Siendo K el vertice superior izquierdo $TEX: \[<br />\begin{gathered}<br /> \sum\limits_{i = 1}^{n - 1} {k + i(n + 1)} \hfill \\<br /> kn + (n + 1)\sum\limits_{i = 1}^{n - 1} i \hfill \\<br /> kn + \frac{{n(n + 1)(n - 1)}}<br />{2} \hfill \\<br /> kn + \frac{{n(n^2 - 1)}}<br />{2} \hfill \\ <br />\end{gathered} <br />\]<br />$ Luego reemplazamos n=27 y tenemos $TEX: \[<br />6202 \bullet 27 + \frac{{27 \bullet 728}}<br />{2} = 167454 + 9828 = 177282<br />\]<br />$

Guía Rojo Ver Perfil del Miembro Ver los mensajes de este miembro	May 20 2006, 10:56 PM Publicado: #10
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 903 Registrado: 28-May 05 Desde: Santiago, Chile Miembro Nº: 69 Nacionalidad: Colegio/Liceo: Sexo:	CITA(xsebastian @ May 21 2006, 12:47 AM) El aporte de "la semisuma de los extremos = término central" es un truco muy bueno, para resolver toda esta prueba en muy poco tiempo. Así que no debiera mirarse en menos fue una indirecta??... bueno, dejémoslo así... mi argumento para no ocuparlo fue el que tenía que probar algo no muy "lindo", y además, la fórmula nos dio una utilidad muy buena... eso, saludos... -------------------- Bachiller en Ciencias (ex) Estudiante de Medicina Estudiante de Ingeniería Civil de Industrias, diploma en Ingeniería Matemática Pontificia Universidad Católica de Chile "El espíritu del matemático busca la belleza del pensamiento, y esa va de la mano con la filosofía." - Héctor Hardy Pastén Vásquez "¿Qué te hace pensar que si tienes dos elementos de un conjunto con otros dos elementos de otro conjunto se origina uno nuevo con cuatro? Es sólo el sentido común, no te imaginas que los elementos aparecen de la nada, pero resulta que con el sólo hecho de cuestionar el sentido común, se podría afirmar que cuando juntas cuatro elementos aparecen miles de elementos más. Y si lo demuestras, todo se basa en la razón." - Alonso Duque Vega, razonador por excelencia $TEX: $S=1+dfrac{1}{2}+dfrac{1}{3}+dfrac{1}{4}+dfrac{1}{5}+ldots$$ Esta serie converge! He encontrado una maravillosa demostración de esto, pero no cabe en la estrechez de esta firma...

« Posterior · Segunda Fecha · Anterior »

3 Páginas:

1 2 3 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 09:00 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.