Primer Nivel Individual

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > Campeonato Interescolar > Campeonato Interescolar 2006 > Segunda Fecha

2 Páginas:

1 2 >

Primer Nivel Individual

Opciones

daniel_contreras... daniel_contreras(IN) Ver Perfil del Miembro Ver los mensajes de este miembro	May 20 2006, 08:37 PM Publicado: #1
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 18 Registrado: 15-December 05 Miembro Nº: 470 Nacionalidad: Sexo:	(1) Una pieza de dominó es una fila con dos números, no necesariamente distintos, del conjunto {0,1,2,3,4,5,6} a cada pieza de dominó asociamos la suma de los dos números que contiene, por ejemplo: ¿Cuánto vale la suma de todos los números asociados a las fichas de dominó? (2) Se tiene la siguiente sucesión de triángulos. Encuentre el valor de N.

Imperious Ver Perfil del Miembro Ver los mensajes de este miembro	May 20 2006, 09:01 PM Publicado: #2
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 23 Registrado: 12-July 05 Desde: I.N. Miembro Nº: 140 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: P2 Primero fijemonos y esto es muy importante, ya que los numeros que estan en la base, si los sumamos nos dara el n° total de triangulos <br />De esta forma en el primero 1+3=4 y por consiguiente el numero qu esta en la punta va a ser 4.<br />Ahora para el triangulo que nos piden tenemos que sumar de 1+...+99, pero tambien cabe destacar que los numeros que estan en la base son impares consecutivos.<br />Ahora para sumar estos numeros haremos lo siguiente: vamos a agrupar el 1 con el 99, el 3 con el 97 y asi sucesivamente durante la suma, tal que van haber 25 agrupaciones, estan agrupaciones se hacen para hacer mas facil la suma tal que, 1+99=100, 3+97=100 y asi sucesivamente.<br />Tal que la suma es 25*100 y eso es 2500<br />Entonces n=2500 <br />$ --------------------

Cesarator	May 20 2006, 10:39 PM Publicado: #3
Invitado	Solución perfecta al P2. Sólo indicar que seguramente muchos llegaron a la respuesta 2500, pero estoy seguro que muchos cayeron en la tentación de "justificarlo" poniendo simplemente que será el cuadrado de 50... ¡Eso había que justificarlo rotundamente! Recordar que respuestas con poca justificación tienen penalización en puntaje.

caf_tito Ver Perfil del Miembro Ver los mensajes de este miembro	May 20 2006, 11:04 PM Publicado: #4
Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.605 Registrado: 25-June 05 Miembro Nº: 123 Colegio/Liceo: Universidad: Sexo:	viendo el ejercicio, creo que como justificó imperious, también nos podemos dar cuenta que para sacar, el numerito de arriba $TEX: n$ en función al último número de la base (nombrémolo 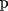$TEX: p$ ) $TEX: \[<br />n = \left( {\frac{{p + 1}}<br />{2}} \right)^2 <br />\]$ y he ahí otra solución xD (ojalá q en primero medio se me hubiera ocurrido xD) --------------------

Corecrasher	May 21 2006, 09:08 AM Publicado: #5
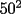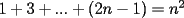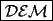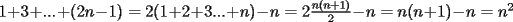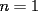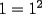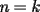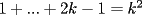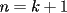Invitado	Basta recordar la sumatoria de impares para justificar lo de $TEX: $50^2$$ $TEX: $\boxed{\mathcal{SUM}}$$ $TEX: $1+3+...+(2n-1)=n^2$$ $TEX: $\boxed{\mathcal{DEM}}$$ Sin induccion: $TEX: $1+3+...+(2n-1)=2(1+2+3...+n)-n=2\frac{n(n+1)}{2}-n=n(n+1)-n=n^2$$ . Con induccion: Para $TEX: $n=1$$ se cumple $TEX: $1=1^2$$ Para $TEX: $n=k$$ diremos que tambien , osea $TEX: $1+...+2k-1=k^2$$ Para $TEX: $n=k+1$$ tenemos $TE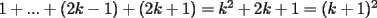X: $1+...+(2k-1)+(2k+1)=k^2+2k+1=(k+1)^2$$ . En el problema tenemos el caso particular de 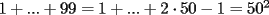$TEX: $1+...+99=1+...+2\cdot50-1=50^2$$

Killua Ver Perfil del Miembro Ver los mensajes de este miembro	May 21 2006, 08:03 PM Publicado: #6
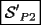Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Mi solución fue parecida a la de Imperious, aquí está: 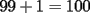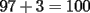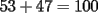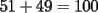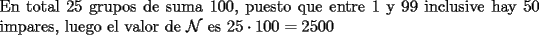$TEX: $\boxed{\mathcal{S'}_{P2}}$$ $TEX: \noindent Notemos que el n\'umero de la punta de los tri\'angulos, en nuestro problema $\mathcal{N}$, corresponde al n\'umero de triangulitos que hay, llam\'emosle casillas. Ahora bien, notemos que en el primer "piso" del tri\'angulo hay un n\'umero impar de casillas, y en el segundo piso hay una cantidad de casillas correspondientes al impar antecesor del primer piso, y as\'i sucesivamente con los otros pisos.$ $TEX: \noindent Ahora, en nuestro tri\'angulo, en el primer piso hay $99$ casillas, en el segundo $97$, en el tercero $95$, y as\'i hasta llegar al piso donde esta $\mathcal{N}$. Luego, $\mathcal{N}$ corresponde a $99+97+...+3+1$, para calcular esta suma, haremos algo similar a lo que hizo Gauss, o sea sumar el primero con el \'ultimo, el segundo con el pen\'ultimo, y as\'i sucesivamente, teniendo:$ $TEX: $99+1=100$$ $TEX: $97+3=100$$ ... $TEX: $53+47=100$$ $TEX: $51+49=100$$ $TEX: \noindent En total $25$ grupos de suma $100$, puesto que entre $1$ y $99$ inclusive hay $50$ impares, luego el valor de $\mathcal{N}$ es $25\cdot{100}=2500$$ Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy) "A mathematician is a device for turning coffee into theorems" (Paul Erdös)

Imperious Ver Perfil del Miembro Ver los mensajes de este miembro	May 22 2006, 09:33 AM Publicado: #7
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 23 Registrado: 12-July 05 Desde: I.N. Miembro Nº: 140 Nacionalidad: Colegio/Liceo: Sexo:	CITA(Killua @ May 21 2006, 09:03 PM) Mi solución fue parecida a la de Imperious, aquí está: $TEX: $\boxed{\mathcal{S'}_{P2}}$$ $TEX: \noindent Notemos que el n\'umero de la punta de los tri\'angulos, en nuestro problema $\mathcal{N}$, corresponde al n\'umero de triangulitos que hay, llam\'emosle casillas. Ahora bien, notemos que en el primer "piso" del tri\'angulo hay un n\'umero impar de casillas, y en el segundo piso hay una cantidad de casillas correspondientes al impar antecesor del primer piso, y as\'i sucesivamente con los otros pisos.$ $TEX: \noindent Ahora, en nuestro tri\'angulo, en el primer piso hay $99$ casillas, en el segundo $97$, en el tercero $95$, y as\'i hasta llegar al piso donde esta $\mathcal{N}$. Luego, $\mathcal{N}$ corresponde a $99+97+...+3+1$, para calcular esta suma, haremos algo similar a lo que hizo Gauss, o sea sumar el primero con el \'ultimo, el segundo con el pen\'ultimo, y as\'i sucesivamente, teniendo:$ $TEX: $99+1=100$$ $TEX: $97+3=100$$ ... $TEX: $53+47=100$$ $TEX: $51+49=100$$ $TEX: \noindent En total $25$ grupos de suma $100$, puesto que entre $1$ y $99$ inclusive hay $50$ impares, luego el valor de $\mathcal{N}$ es $25\cdot{100}=2500$$ Saludos jaja es casi casi igual jaja pero estuvo bien igual --------------------

{ .HERCULES. } Ver Perfil del Miembro Ver los mensajes de este miembro	May 23 2006, 04:02 PM Publicado: #8
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 24 Registrado: 1-April 06 Desde: Estacion Central , Santiago Miembro Nº: 744 Nacionalidad: Colegio/Liceo: Sexo:	Respecto a el problema 1 esta es mi solucion : primero tenemos que ver todas las fichas que contengan 0 : 0-1,0-2,0-3,0-4,0-5,0-6 . Los numeros asociados son : 1+2+3+4+5+6=21 Ahora vemos los numeros con 1 : 1-1,1-2,1-3,1-4,1-5,1-6. Los numeros asociados son : 2+3+4+5+6+7=27 Ahora los con 2: 2-2,2-3,2-4,2-5,2-6. Los numeros asociados son : 4+5+6+7+8=30 Ahora los con 3: 3-3,3-4,3-5,3-6. Los numeros asociados son : 6+7+8+9=30 Ahora los con 4 : 4-4,4-5,4-6. Los numeros asociados son: 8+9+10=27 Ahora los con 5: 5-5,5-6. Los numeros asociados son : 10+11=21 Y por ultimo los con 6: 6-6. Y el numero asociado es : 12 Entonces :21+27+30+30+27+21+12= 168 -------------------- Si puedes bromear sobre algo muy importante , es porque haz alcanzado la libertad

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	May 23 2006, 06:49 PM Publicado: #9
Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	El procedimiento y la respuesta están correctos, pero se puede acortar la solución, y esa es la idea, ver si hay una solución más breve, evitar sumarlos todos -------------------- Sebastián Elías Puelma Moya Administrador FMAT

Tygger evolution Ver Perfil del Miembro Ver los mensajes de este miembro	May 26 2006, 06:38 PM Publicado: #10
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 25 Registrado: 19-August 05 Desde: santiago chile Miembro Nº: 255 Nacionalidad: Sexo:	Notemos q que el "1" esta 8 veces: 1-0, 1-1, 1-2, 1-3, 1-4, 1-5, 1-6 y esto mismo ocurrira con 2, 3, 4, 5, 6, luego obtendremos q cada numero estara repetido 8 vesces y tendremos la suma siguiente: (1x8)+(2x8)+(3x8)+(4x8)+(5x8)+(6x8) 8(1+2+3+4+5+6) 8x21 168 por lo tanto la suma es 168 saludos -------------------- Por aqui paso Tygger SS.CC Fco Garrido

« Posterior · Segunda Fecha · Anterior »

2 Páginas:

1 2 >

2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 08:56 PM