|
|
|
|
|
|
|
  |
 May 9 2006, 10:43 AM May 9 2006, 10:43 AM
Publicado:
#1
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
6ª OLIMPIADA DE MAYO Segundo Nivel Problema 1: El conjunto 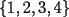 puede ser partido en dos subconjuntos puede ser partido en dos subconjuntos 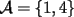 y y 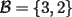 sin elementos comunes y tales que la suma de los elementos de sin elementos comunes y tales que la suma de los elementos de 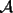 es igual a la suma de los elementos de es igual a la suma de los elementos de 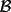 . Una tal partición es imposible para el conjunto . Una tal partición es imposible para el conjunto 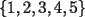 y también para el conjunto y también para el conjunto 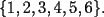 Determinar todos los valores de Determinar todos los valores de  para los que el conjunto de los primeros para los que el conjunto de los primeros  números naturales puede ser partido en dos subconjuntos sin elementos comunes tales que la suma de los elementos de cada subconjunto sea la misma. números naturales puede ser partido en dos subconjuntos sin elementos comunes tales que la suma de los elementos de cada subconjunto sea la misma.Problema 2: En un paralelógramo de área 1 se trazan las rectas que unen cada vértice con el punto medio de cada lado no adyacente a él. Las ocho rectas trazadas determinan un octógono en el interior del paralelógramo. Calcular el área de dicho octógono. Problema 3: Sean 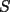 una circunferencia de radio 2; una circunferencia de radio 2; 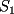 una circunferencia de radio 1 tangente interiormente a una circunferencia de radio 1 tangente interiormente a 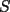 en en 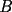 y y 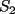 una circunferencia de radio 1 tangente a una circunferencia de radio 1 tangente a 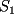 en el punto en el punto 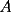 pero que no es tangente a pero que no es tangente a 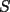 . Si . Si 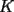 es el punto de intersección de la recta es el punto de intersección de la recta 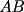 con la circunferencia con la circunferencia 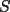 , demostrar que , demostrar que 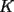 pertenece a la circunferencia pertenece a la circunferencia 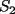 . .Problema 4: Se tiene un cubo de 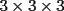 formado por la unión de 27 cubitos de formado por la unión de 27 cubitos de 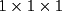 . Se retiran algunos cubitos de tal modo que los que permanecen siguen formando un sólido constituido por cubitos que están unidos por lo menos por una cara al resto del sólido. Cuando se retira un cubito los que permanecen lo hacen en el mismo lugar en que estaban. ¿Cuál es el máximo número de cubitos que se pueden retirar de modo que el área del sólido que resulta sea igual al área del cubo original? . Se retiran algunos cubitos de tal modo que los que permanecen siguen formando un sólido constituido por cubitos que están unidos por lo menos por una cara al resto del sólido. Cuando se retira un cubito los que permanecen lo hacen en el mismo lugar en que estaban. ¿Cuál es el máximo número de cubitos que se pueden retirar de modo que el área del sólido que resulta sea igual al área del cubo original?Problema 5: Un rectángulo se puede dividir en  cuadrados iguales y también se puede dividir en cuadrados iguales y también se puede dividir en 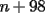 cuadrados iguales. Si el área del rectángulo es cuadrados iguales. Si el área del rectángulo es  , con , con  entero, hallar los lados del rectángulo. Dar todas las posibilidades. entero, hallar los lados del rectángulo. Dar todas las posibilidades.Resumen de soluciones -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 May 11 2006, 02:36 PM May 11 2006, 02:36 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 670 Registrado: 30-January 06 Desde: Ñuñoa, Santiago Miembro Nº: 524 Nacionalidad:  Universidad:  Sexo:  |
![TEX: <br />\[<br />\begin{gathered}<br /> {\text{P1) Sea C el conjunto 1}}{\text{,2}}{\text{,3}}{\text{,4}}{\text{,5}},...,{\text{n}} \hfill \\<br /> {\text{La suma de los miembros de C debe ser divisible por 2 para poder ser dividido}} \hfill \\<br /> {\text{en grupos de igual suma}}{\text{, entonces:}} \hfill \\<br /> \frac{C}<br />{2} = \frac{{1 + 3 + 4 + 5 + ... + n}}<br />{2}{\text{ debe ser entero}}{\text{, pero esta suma se puede escribir como:}} \hfill \\<br /> \frac{{\text{C}}}<br />{{\text{2}}} = \frac{{\frac{{n(n + 1)}}<br />{2}}}<br />{2} = \frac{{n(n + 1)}}<br />{4}{\text{ que debe ser un entero}}{\text{. Entonces n \'o (n + 1) deben ser m\'u ltiplos de 4}} \hfill \\<br /> {\text{(no pueden ser ambos a la vez ya que un m\'ultiplo de 4}}{\text{, m\'as 1}}{\text{, no es m\'ultiplo de 4)}} \hfill \\<br /> n \equiv 0(\bmod 4) \hfill \\<br /> {\text{o}} \hfill \\<br /> n + 1 \equiv 0(\bmod 4) \Rightarrow n \equiv 3(\bmod 4) \hfill \\<br /> {\text{Entonces}}{\text{, los valores posibles para n son los m\'ultiplos positivos de 4 o sus antecesores:}} \hfill \\<br /> n = \left\{ {3,4,7,8,11,12,15,16,...,(4k - 1),4k,...} \right\}{\text{ donde k}} \in {\text{N}}{\text{.}} \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/63662.gif)
--------------------    |
|
|
|
 May 13 2006, 04:31 PM May 13 2006, 04:31 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Lo que hiciste, fue descartar todos los valores de
 , congruentes con 2 o bien con 3, en módulo 4. Lo que viene ahora, es considerar cualquier número congruente con 0 o bien con 1, en módulo 4, y mostrar cómo se puede partir , congruentes con 2 o bien con 3, en módulo 4. Lo que viene ahora, es considerar cualquier número congruente con 0 o bien con 1, en módulo 4, y mostrar cómo se puede partir 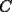 en dos subconjuntos con la misma suma. en dos subconjuntos con la misma suma.
-------------------- |
|
|
|
 May 3 2007, 09:33 PM May 3 2007, 09:33 PM
Publicado:
#4
|
|
 Principiante Matemático Grupo: Usuario FMAT Mensajes: 5 Registrado: 29-April 07 Desde: Asunción, Paraguay Miembro Nº: 5.523 Nacionalidad:  Sexo:  |
Problema 3
Intente hacerla de la forma mas corta posible...Pero no pude!!! Aca va mi respuesta, quiero saber su opinion. Como el punto B no pertenece a la tangente de las Circunferencias S1 y S2, entonces, la Recta AB corta en 2 puntos a la Circunferencia S2. Uno, como plantea el problema es A (por ser punto de tangencias, pertenece a la Circunferencia), y el otro es un punto al que llame N. Entonces, tenemos que N pertenece a BA y a S2. Llame a los centros de las Circunferencias S, S1 y S2, O, O1 y O2, respectivamente. En la Circunferencia S1 trazamos BO1=O1A (por ser ambos radios). Asi obtenemos un triangulo isosceles O1AB, con los angulos ABO1=x=BAO1; y el angulo BO1A=y. Analogamente, encontramos en S2 el triangulo isosceles O2AN, con los angulos O2NA=O2AN=BAO1=x (opuestos por el vertice). Entonces el angulo AO2N=y. Los triangulos O1BA y O2AN son congruentes por tener angulos iguales y 2 lados iguales (los radios=1). Por lo tanto BA=AN, A es punto medio de BN Por otra parte vemos lo siguiente: K pertenece a S y a AB.Trazamos OK y OB y formamos el triangulo isoscles OKB. Como O1B es perpendicular a la Tangente BE (E siendo un punto en la tangente a S1 y S) , y BO tambien es perpendicular a BE, BO1O es una sola recta. Como K pertenece a AB, y O1 a BO, entonces el angulo OBK=O1BA=x. Como el triangulo OBK es isosceles con OB=OK, entonces, el angulo OKB=x tambien; posteriormente vemos que el angulo KOB=y. (Ahora va a ser imperativo para entender el problema que hagan el grafico que voy a describir) Trazan la recta BK, con A y N en la recta. Necesitamos trazar tambien:OB con O1 en la recta, ON y OK. BA=AN, O1B=O1O. Entonces, O1A es base media de OBN. Por lo tanto es paralela a ON. Entonces el angulo ONB=O1AB=x. El angulo ONB=OKB+KON. ONB=x, OKB=x. Entonces, KON=0, por lo tanto K y N coinciden, Saludos, Ariel S P.D.: Al escribir esto me di cuenta de un error y cambie mi solucion, por eso tal vez haya algunos datos inutiles en el camino...Me olvide de marcar los subindices, espero que aun asi se entienda. -------------------- "Hay una fuerza motriz más poderosa que el vapor, la electricidad y la energía atómica: la Voluntad."
Albert Einstein |
|
|
|
 May 4 2007, 08:28 AM May 4 2007, 08:28 AM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
La solución es correcta, aunque cuesta un poco seguirla. Es ideal acompañar las soluciones en geometría con una imagen, que explique mejor lo que está sucediendo, y también respetar los subíndices. El comentario más importante, sn embargo, es simplificar más la solución, creo que se puede hacer eso
Saludos -------------------- |
|
|
|
 May 4 2007, 08:29 PM May 4 2007, 08:29 PM
Publicado:
#6
|
|
 Principiante Matemático Grupo: Usuario FMAT Mensajes: 5 Registrado: 29-April 07 Desde: Asunción, Paraguay Miembro Nº: 5.523 Nacionalidad:  Sexo:  |
Gracias por la opinion honesta. Ese era el primer mensaje que envie a este foro y me va a tomar tiempo adaptarme a toda la simbologia. Pero si la respuesta esta bien (o mas o menos bien) ya me pone feliz.
Saludos Ariel S -------------------- "Hay una fuerza motriz más poderosa que el vapor, la electricidad y la energía atómica: la Voluntad."
Albert Einstein |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 09:19 PM |









