|
|
|
|
|
|
|
  |
 Apr 22 2006, 08:57 PM Apr 22 2006, 08:57 PM
Publicado:
#1
|
|
 Principiante Matemático Grupo: Usuario FMAT Mensajes: 8 Registrado: 7-August 05 Desde: maipú santiago Miembro Nº: 184 |
Aqui dejo la nueva version(segundo escaneo) del Nivel 4 CMAT

-------------------- "Las matemáticas no mienten, lo que hay son muchos matemáticos mentirosos."
Pam |
|
|
|
 Apr 22 2006, 09:55 PM Apr 22 2006, 09:55 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 670 Registrado: 30-January 06 Desde: Ñuñoa, Santiago Miembro Nº: 524 Nacionalidad:  Universidad:  Sexo:  |
![TEX: <br />\[<br />\begin{gathered}<br /> {\text{(1) a) Notemos que el total de numeros distintos de cero es 20*20 = 400}}{\text{, es decir}}{\text{, los numeros van}} \hfill \\<br /> {\text{del 1 al 400. Ademas}}{\text{, cada numero se encuentra sumado 4 veces al total}} \hfill \\<br /> {\text{(una en cada vertice propio)}}{\text{, entonces lo que tenemos es una sumatoria:}} \hfill \\<br /> S = \sum\limits_{i = 1}^{400} {4i} = S = 4\sum\limits_{i = 1}^{400} i = 4*\frac{{(400 + 1)*400}}<br />{2} = 4*401*200 = {\text{320}}{\text{.800}} \hfill \\<br /> {\text{Que es la suma de todos los numeros en los vertices}} \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/58514.gif) ![TEX: <br />\[<br />\begin{gathered}<br /> {\text{b) En este caso}}{\text{, debemos primero calcular el total de numeros del triangulo}}{\text{.}} \hfill \\<br /> {\text{Notamos que la cantidad de numeros en cada nivel es la sucesion de los numeros impares}}{\text{.}} \hfill \\<br /> {\text{Entonces}}{\text{, si hay 22 pisos}}{\text{, el total de numeros es:}} \hfill \\<br /> N = \sum\limits_{i = 1}^{22} {2i - 1} = 2\sum\limits_{i = 1}^{22} i - \sum\limits_{i = 1}^{22} 1 = 2*\frac{{(22 + 1)*22}}<br />{2} - 22 = 23*22 - 22 = 22^2 = 484 \hfill \\<br /> {\text{O sea que los numeros van del 1 al 484}}{\text{. Ahora notamos que cada numero se encuentra}} \hfill \\<br /> {\text{sumado tres veces (una en cada uno de sus vertices)}}{\text{. Nuevamente el total es una sumatoria:}} \hfill \\<br /> S = \sum\limits_{i = 1}^{484} {3i} = 3\sum\limits_{i = 1}^{484} i = 3*\frac{{(484 + 1)*484}}<br />{2} = 3*485*242 = 352.110 \hfill \\<br /> {\text{Que es el total de la suma de los vertices del triangulo}} \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/58484.gif)
--------------------    |
|
|
|
 Apr 22 2006, 10:11 PM Apr 22 2006, 10:11 PM
Publicado:
#3
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
CITA(fs_tol @ Apr 22 2006, 10:55 PM) La solucion es correcta Por cierto en latex en ver de 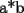 , te recomiendo $a\cdot b$ que genera , te recomiendo $a\cdot b$ que genera 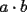 Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Apr 23 2006, 01:49 AM Apr 23 2006, 01:49 AM
Publicado:
#4
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Aca les dejo una posible solucion al P2, que corresponde al lema que use para desarrollar otro problema de un poco mas complejidad.
http://www.fmat.cl/index.php?showtopic=136...findpost&p=8985 Logicamente no era la idea de la prueba "matar una mosquita a cañonazos" pero al menos les dejo el interes de aprender el famoso Teorema de Ptolomeo... Esperemos que alguien postee alguna solucion que no lo use...y anticipo que hay muchas formas de resolver este problema sin usarlo (de hecho a eso apuntaba el cmat). Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Apr 23 2006, 09:40 AM Apr 23 2006, 09:40 AM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 519 Registrado: 22-April 06 Desde: Concepción Miembro Nº: 925 Nacionalidad:  Sexo:  |
esto es lo que yo puse en el P2
 los triángulos 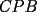 y y 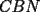 son semejantes por el ángulo común son semejantes por el ángulo común 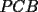 y los ángulos y los ángulos 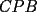 y y 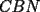 que miden 60º. que miden 60º.Luego 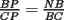 , y de la misma manera , y de la misma manera 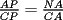 . Sumando y viendo que el triángulo es equilátero, . Sumando y viendo que el triángulo es equilátero, 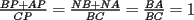 , y , y 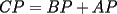 . .No está muy bien escrito, pero éste es mi primer post Para la otra mejorará -------------------- There is a theory which states that if ever anyone discovers exactly what the Universe is for and why is it here, it will instantly disappear and be replaced by something even more bizarre and inexplicable.
There is another theory which states that this has already happened. - Adams, The Restaurant at the End of the Universe ----------------------------------- Existe una teoría que postula que si alguien alguna vez llega a descubrir exactamente para qué es el Universo y por qué está aquí, éste desaparecerá instantáneamente y será reemplazado por algo aún más extraño e inexplicable. Existe otra teoría que dice que esto ya ha ocurrido. - Adams, el Restorán al Final del Universo |
|
|
|
 Apr 23 2006, 01:42 PM Apr 23 2006, 01:42 PM
Publicado:
#6
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 270 Registrado: 29-August 05 Desde: rancagua Miembro Nº: 277 Nacionalidad:  Sexo:  |
yo el problema uno hize todo el razonamiento logico....pero mi unico gran problema es que no sabia que
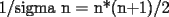 si no fuera por eso tendria esos 10 puntos seguros.....y el dos no tenia idea como hacerlo si no fuera por eso tendria esos 10 puntos seguros.....y el dos no tenia idea como hacerloAAAAAAAAAA no se usar latex -------------------- todo lo que no es eterno es eternamente inútil
 |
|
|
|
 Apr 23 2006, 09:52 PM Apr 23 2006, 09:52 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Vean aquí una nueva solución, me refiero al resultado 2
Observen que estaba resuelto en este foro, antes que apareciera en la prueba -------------------- |
|
|
|
 Apr 24 2006, 12:41 AM Apr 24 2006, 12:41 AM
Publicado:
#8
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
CITA(†Alucard† @ Apr 23 2006, 10:40 AM) esto es lo que yo puse en el P2  los triángulos 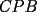 y y 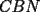 son semejantes por el ángulo común son semejantes por el ángulo común 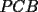 y los ángulos y los ángulos 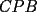 y y 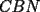 que miden 60º. que miden 60º.Luego 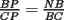 , y de la misma manera , y de la misma manera 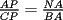 . Sumando y viendo que el triángulo es equilátero, . Sumando y viendo que el triángulo es equilátero, 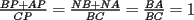 , y , y 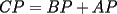 . .No está muy bien escrito, pero éste es mi primer post Para la otra mejorará Solo un leve detallito... Aca CITA 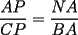 deberia ser... 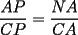 Igual da lo mismo por que el triangulo es equilatero, pero es importante para que se entienda la semejanza... Respecto a tu solucion, esta muy bonita, y te felicito...me gusto por la simpleza y elegancia... Mis saludos y bienvenido a fmat -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Apr 24 2006, 08:09 PM Apr 24 2006, 08:09 PM
Publicado:
#9
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 336 Registrado: 26-May 05 Desde: Pte Asalto Miembro Nº: 63 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
CITA(†Alucard† @ Apr 23 2006, 10:40 AM) esto es lo que yo puse en el P2  los triángulos 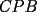 y y 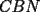 son semejantes por el ángulo común son semejantes por el ángulo común 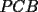 y los ángulos y los ángulos 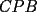 y y 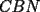 que miden 60º. que miden 60º.Luego 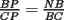 , y de la misma manera , y de la misma manera 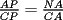 . Sumando y viendo que el triángulo es equilátero, . Sumando y viendo que el triángulo es equilátero, 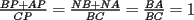 , y , y 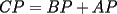 . .No está muy bien escrito, pero éste es mi primer post Para la otra mejorará Entiendo xq el ángulo 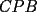 mide 60º pero no está explicado por qué... mide 60º pero no está explicado por qué...Para mi es porque inscribe el mismo arco que el angulo 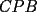 y lo Mismo pasa con el ángulo y lo Mismo pasa con el ángulo 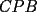 yel ángulo yel ángulo  eso quería aclararlo porque al comienzo me produjo dudas verlo asi no mas y tuve que reflexionarlo un rato... Lo que es yo... ESTOY FELIZ ESPERANDO LA RECUPERATIVA --------------------   |
|
|
|
| Cesarator |
 Jun 8 2006, 12:46 PM Jun 8 2006, 12:46 PM
Publicado:
#10
|
|
Invitado |
Otra solución, completamente diferente a las dadas para el P2, puede verse
es este link: AQUI |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 12th April 2025 - 09:55 AM |










![TEX: <br />\[<br />\begin{gathered}<br /> {\text{(1) Notemos que el total de numeros distintos de cero es 20*20 = 400}}{\text{, es decir}}{\text{, los numeros van}} \hfill \\<br /> {\text{del 1 al 400. Ademas}}{\text{, cada numero se encuentra sumado 4 veces al total}} \hfill \\<br /> {\text{(una en cada vertice propio)}}{\text{, entonces lo que tenemos es una sumatoria:}} \hfill \\<br /> S = \sum\limits_{i = 1}^{400} {4i} = S = 4\sum\limits_{i = 1}^{400} i = 4*\frac{{(400 + 1)*400}}<br />{2} = 4*401*200 = {\text{320}}{\text{.800}} \hfill \\<br /> {\text{Que es la suma de todos los numeros en los vertices}} \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/58382.gif)

