Segundo Nivel Individual - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > Campeonato Interescolar > Campeonato Interescolar 2006 > Primera Fecha

Reply to this topic

Start new topic

Segundo Nivel Individual

Rurouni Kenshin Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 22 2006, 07:59 PM Publicado: #1
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad: Sexo:	screen.width0.6) {this.resized=true; this.width=screen.width0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaÃ±o original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img88.imageshack.us/img88/8328/cmat20xs.jpg');}" /> Saludos y buena suerte -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!) Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)

Killua Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 22 2006, 08:10 PM Publicado: #2
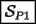Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	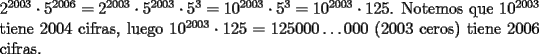$TEX: $\boxed{\mathcal{S}_{P1}}$$ $TEX: \noindent Notemos que:$ $TEX: \noindent$2^{2003}\cdot{5}^{2006}=2^{2003}\cdot{5}^{2003}\cdot{5}^3=10^{2003}\cdot{5^3}=10^{2003}\cdot{125}$. Notemos que $10^{2003}$ tiene $2004$ cifras, luego $10^{2003}\cdot{125}=125000\ldots{0}00$ ($2003$ ceros) tiene $2006$ cifras.$ Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy) "A mathematician is a device for turning coffee into theorems" (Paul Erdös)

Rurouni Kenshin Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 22 2006, 08:11 PM Publicado: #3
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad: Sexo:	CITA(Killua @ Apr 22 2006, 09:10 PM) $TEX: $\boxed{\mathcal{S}_{P1}}$$ $TEX: \noindent Notemos que:$ $TEX: \noindent$2^{2003}\cdot{5}^{2006}=2^{2003}\cdot{5}^{2003}\cdot{5}^3=10^{2003}\cdot{5^3}=10^{2003}\cdot{125}$. Notemos que $10^{2003}$ tiene $2004$ cifras, luego $10^{2003}\cdot{125}=125000\ldots{0}00$ ($2003$ ceros) tiene $2006$ cifras.$ Saludos Solucion correcta!!! Estaba buscando un problema muy parecido(casi igual) que habia posteado en el foro Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!) Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)

Corecrasher	Apr 22 2006, 10:30 PM Publicado: #4
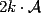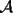Invitado	$TEX: $\boxed{\mathcal{S}_{p2}}$$ Notemos que un patron por si solo no puede rellenar una figura convexa como lo es un rectangulo, pero si $TEX: $2$$ patrones ; en general un numero par de patrones puede y un impar deja un pedacito sin rellenar. 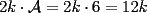En consecuencia el area cubierta sera $TEX: $2k \cdot \mathcal{A}$$ , donde $TEX: $\mathcal{A}$$ es el area de un patron (por enunciado $TEX: $6$$ ) entonces $TEX: $2k \cdot \mathcal{A}=2k \cdot 6=12k$$ , probando asi lo pedido

Rurouni Kenshin Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 23 2006, 12:24 AM Publicado: #5
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad: Sexo:	CITA(Killua @ Apr 22 2006, 09:10 PM) $TEX: $\boxed{\mathcal{S}_{P1}}$$ $TEX: \noindent Notemos que:$ $TEX: \noindent$2^{2003}\cdot{5}^{2006}=2^{2003}\cdot{5}^{2003}\cdot{5}^3=10^{2003}\cdot{5^3}=10^{2003}\cdot{125}$. Notemos que $10^{2003}$ tiene $2004$ cifras, luego $10^{2003}\cdot{125}=125000\ldots{0}00$ ($2003$ ceros) tiene $2006$ cifras.$ Saludos Respecto al P1, solo comentar este link http://www.fmat.cl/index.php?showtopic=2187 Posteado el Mar 2 2006, 12:18 AM Nivel Principiante, Subseccion Basica, en los resueltos... Saludos PD: El problema posteado por mi es un poco mas dificil, pues tenia que usarse ademas que 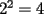$TEX: $2^2=4$$ , en cambio en este problema la conclusion era inmediata...(dado que se los pusieron con un 2 y un 5 de una ) -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!) Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)

Cesarator	Apr 23 2006, 09:18 PM Publicado: #6
Invitado	sólo decir que difícilmente le asignaría un buen puntaje a una respuesta como la dada por corecrasher al problema 2. Supongo que en la prueba se justificó un poco más.

Cesarator	Apr 26 2006, 07:38 AM Publicado: #7
Invitado	Insisto que falta justificar un poco más la solución al problema de los patrones. Específicamente, la parte de que se necesita un número par de patrones para formar un rectángulo, que es clave.

Wiccans Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 28 2006, 04:01 PM Publicado: #8
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 16 Registrado: 21-April 06 Miembro Nº: 897	El problema de los patrones es facil de esplicar (aunque me alla equivocado en la prueba)... un rectangulo apatronado siempre va a tener un lado par, solo basta que se pongan 6 rectangulos apatronados seguidos desde el lado par y esto sera un multiplo de 12... --------------------

Zirou Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 28 2006, 06:38 PM Publicado: #9
Máquina que convierte café en teoremas Grupo: Colaborador Silver Mensajes: 1.665 Registrado: 18-August 05 Desde: Concepción Miembro Nº: 247 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	mmm el patron juntandolo con el patron girado de 180º forma un rectangulo de 43 unidades y la area de esa es doce. esta es la unica forma de formar rectangulos, osea ccon un numero par de patrones ya que si este no es el caso, el rectangulo no quedarA completo por la forma del patron, como cada patron tiene como area 6 y como se necesita un numero par de patrones la formula queda asi: 6(2n)=12n 6= area del patron 2n expresa el numero par de patron qed que a traves de los patrones el area del rectangulo sera multiplo de 12. -------------------- $TEX: $mathcal{Z}$ $imath$ $Re$ $varnothing$ $mho$$ Manual para subir imágenes y archivos* a fmat (con servidor propio) Manual de latex Estilo Propio Lista de libros en fmat "Un Matemático es una máquina que trasforma café en teoremas"(Erdös) --- Consultas, sugerencias, reclamos via mp o a los correos mencionados.

FelipeX300 Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 20 2008, 11:53 PM Publicado: #10
Principiante Matemático Grupo: Usuario FMAT Mensajes: 7 Registrado: 10-June 08 Miembro Nº: 26.800 Nacionalidad: Colegio/Liceo: Sexo:	tema añejo lo se ya resuelto lo se sin sentido lo que pondre lo se pero igual el problema 1 lo hize de otra forma $TEX: <br />\[<br />2^n = \frac{n}<br />{3}cifras<br />\]<br />$ pero con la condicion de que todo resto se aproxima osea si da por ejemplo n/3=0.3= 1 cifra asi nos da que $TEX: \[<br />\begin{gathered}<br /> 2^2 = \frac{2}<br />{3}cifras = 1cifra = 4 \hfill \\<br /> 2^3 = \frac{3}<br />{3}cifras = 1cifra = 8 \hfill \\<br /> 2^4 = \frac{4}<br />{3}cifras = 2cifras = 16 \hfill \\<br /> 2^5 = \frac{5}<br />{3}cifras = 2cifras = 32 \hfill \\<br /> 2^6 = \frac{6}<br />{3}cifras = 2cifras = 64 \hfill \\<br /> 2^7 = \frac{7}<br />{3}cifras = 3cifras = 128 \hfill \\ <br />\end{gathered} <br />\]<br />$ y porlotanto $TEX: \[<br />2^{2003} = \frac{{2003}}<br />{3}cifras = 668cifras<br />\]<br />$ luego notemos que 5 sube una cifra por unidad del exponente pero cada 3 unidades del exponente se mantiene el numero de cifras analizemos los casos $TEX: \[<br />\begin{gathered}<br /> 5^1 = 5 \hfill \\<br /> 5^2 = 25 \hfill \\<br /> 5^3 = 125 \hfill \\<br /> 5^4 = 625 \hfill \\<br /> 5^5 = 3125 \hfill \\<br /> 5^6 = 15625 \hfill \\<br /> 5^7 = 78125 \hfill \\ <br />\end{gathered} <br />\]<br />$ asi tenemos como formula general $TEX: \[<br />5^n = n - \frac{n}<br />{3}cifras<br />\]<br />$ pero: -los resultados de las divisiones por 3 no son aproximables en ningun caso - para las potencias con exponente divisible por 3 ocuparemos el numero del exponente siguiente por ejemplo $TEX: <br />\[<br />\begin{gathered}<br /> 5^3 = 3 - \frac{3}<br />{3}cifras = 2cifras \ne 125 \hfill \\<br /> 5^3 = 4 - \frac{4}<br />{3}cifras = 3cifras = 125 \hfill \\ <br />\end{gathered} <br />\]<br />$ y a lo pedido $TEX: \[<br />5^{2006} = 2006 - \frac{{2006}}<br />{3}cifras = 2006 - 668cifras = 1338cifras<br />\]<br />$ luego por estar siendo multiplicados ambos numeros de cifras se sumas y asi $TEX: \[<br />\begin{gathered}<br /> 1338cifras + 668cifras = 2006cifras \hfill \\<br /> 5^{2003} 2^{2003} = 2006cifras \hfill \\ <br />\end{gathered} <br />\]<br />$ ahora los problemas de hacerlo de esta forma era que no se puede determinar cuanto dara la multiplicacion de los primeros numeros de las potencias osea podria haber terminado uno en 2 y otro en 5 y sumar una potencia o uno en 1 y el otro en 1 y no sumar nada asiq bueno he ahi mi metodo bastante inutil pero es XD cuidence

« Posterior · Primera Fecha · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 6th March 2025 - 09:55 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.