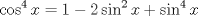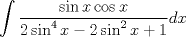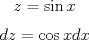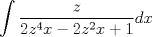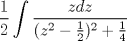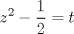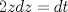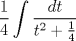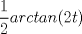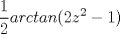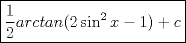Propuesto n.1 - Foro fmat.cl

Propuesto n.1, Integralilla nivel normal

Zero c00l Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 6 2008, 03:12 PM Publicado: #1
Maestro Matemático Grupo: Usuario FMAT Mensajes: 73 Registrado: 18-May 08 Miembro Nº: 23.529 Nacionalidad: Universidad: Sexo:	$TEX: <br />\[<br />\int {} \frac{{\sin x\cos ^{} x}}<br />{{\sin ^4 x + \cos ^4 x}}dx<br />\]<br />$

Montag Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 30 2009, 07:15 PM Publicado: #2
Maestro Matemático Grupo: Usuario FMAT Mensajes: 77 Registrado: 16-July 09 Desde: Scuni Miembro Nº: 55.693 Nacionalidad: Universidad: Sexo:	$TEX: $\displaystyle\int{\dfrac{\sin{x}\cos{x}}{\sin^4{x}+\cos^4{x}}}dx$\\<br /><br />considerando la identidad: $\sin{2x} = 2\sin{x}\cos{x}$ \\<br /><br /><br />$\dfrac{1}{2}\displaystyle\int{\dfrac{\sin{2x}}{(\sin^2{x})^2+(\cos^2{x})^2}}dx$ = $\displaystyle2\int{\dfrac{\sin{2x}}{(1-\cos{2x})^2+(1+\cos{2x})^2}}dx$ =\\<br /><br />$ \displaystyle-\int{\dfrac{d(\cos{2x})}{(1-\cos{2x})^2+(1+\cos{2x})^2}}$=\\<br /><br /><br />$\displaystyle-\int{\dfrac{1}{(1-t)^2+(1+t)^2}dt}$ = $-\dfrac{1}{2}\displaystyle\int{\dfrac{1}{1+ t^2}dt}$ = $-\dfrac{1}{2}\displaystyle\int{d(\arctan{t})} $\\<br /><br /> <br /><br /> $\displaystyle\int{\dfrac{\sin{x}\cos{x}}{\sin^4{x}+\cos^4{x}}}dx$ = $ -\dfrac{1}{2}\arctan(\cos{2x}) + C$<br /><br />$ -------------------- "Describiendo el movimiento de los electrones" Voluntad,Trabajo, Pasión "Si un cuerpo encuentra otro cuerpo, cuando van entre el centeno...." Departamento de ingenieria eléctrica

m_a_t Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 17 2009, 12:17 AM Publicado: #3
Dios Matemático Grupo: Usuario FMAT Mensajes: 428 Registrado: 4-December 07 Desde: Temuco Miembro Nº: 13.504 Nacionalidad: Universidad: Sexo:	CITA(Zero c00l @ Jul 6 2008, 04:12 PM) $TEX: <br />\[<br />\int {} \frac{{\sin x\cos ^{} x}}<br />{{\sin ^4 x + \cos ^4 x}}dx<br />\]<br />$ $TEX: $$\cos ^4 x=1-2\sin^2 x +\sin^4 x$$$ $TEX: $$\int {} \frac{{\sin x\cos ^{} x}}<br />{{2\sin ^4 x -2\sin^2 x +1}}dx$$$ $TEX: $$z=\sin x$$ $$dz=\cos x dx$$$ $TEX: $$\int {} \frac{{z}}<br />{{2z ^4 x -2z^2 x +1}}dx$$$ $TEX: $$\frac{1}{2} \int \frac{zdz}{(z^2-\frac{1}{2})^2 +\frac{1}{4}}$$$ $TEX: $$z^2-\frac{1}{2}=t$$$ $TEX: $$2zdz=dt$$$ $TEX: $$\frac{1}{4} \int \frac{dt}{t^2 +\frac{1}{4}}$$$ $TEX: $$\frac{1}{2}arctan(2t)$$$ $TEX: $$\frac{1}{2}arctan(2z^2 -1)$$$ $TEX: $$\boxed{\frac{1}{2}arctan(2\sin^2 x -1)+c}$$$ -------------------- Pi con 100.000 digitos... Estudiante de Ingeniería Civil Eléctrica - 5 año (falta poco!!!)