Prueba grupal M4 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > Campeonato Interescolar > Campeonato Interescolar 2008 > Cuarta Fecha

Reply to this topic

Start new topic

Prueba grupal M4, IX Region

Versuchung Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 5 2008, 10:56 PM Publicado: #1
Dios Matemático Grupo: Usuario FMAT Mensajes: 399 Registrado: 14-August 07 Desde: Temuco Miembro Nº: 8.739 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Problema 1 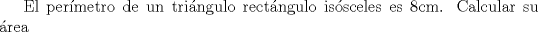$TEX: El perímetro de un triángulo rectángulo isósceles es 8cm. Calcular su área$ Problema 2 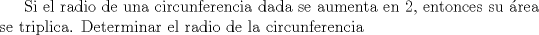$TEX: Si el radio de una circunferencia dada se aumenta en 2, entonces su área se triplica. Determinar el radio de la circunferencia$ Problema 3 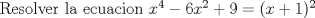$TEX: Resolver la ecuacion $x^{4}-6x^{2}+9= (x+1)^{2}$$ Problema 4 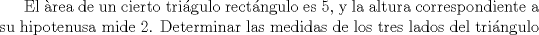$TEX: El àrea de un cierto triágulo rectángulo es 5, y la altura correspondiente a su hipotenusa mide 2. Determinar las medidas de los tres lados del triángulo$ Problema 5 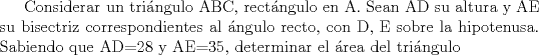$TEX: Considerar un triángulo ABC, rectángulo en A. Sean AD su altura y AE su bisectriz correspondientes al ángulo recto, con D, E sobre la hipotenusa. Sabiendo que AD=28 y AE=35, determinar el área del triángulo$ -------------------- Estudiante Ingeniería Civil Matemática - UFRO 09 Ex Alumna Instituto Victoria - IV° A 08

Versuchung Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 5 2008, 11:56 PM Publicado: #2
Dios Matemático Grupo: Usuario FMAT Mensajes: 399 Registrado: 14-August 07 Desde: Temuco Miembro Nº: 8.739 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	se me olvidaba lo mas notable Pistas (la q mas sirve es la del 5) Pista P1. Los catetos del triangulo deben ser iguales. Pista P2. Plantear una ecuacion cuya incognita sea el radio de la circunferencia. Pista P3. Si 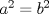$TEX: $a^{2} = b^{2}$$ , entonces a = b o a = -b. Pista P4. El area de un triangulo rectangulo puede calcularse como la mitad del producto de sus catetos. Pista P5. Dar rienda suelta a la creatividad personal... -------------------- Estudiante Ingeniería Civil Matemática - UFRO 09 Ex Alumna Instituto Victoria - IV° A 08

Versuchung Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 7 2008, 10:11 PM Publicado: #3
Dios Matemático Grupo: Usuario FMAT Mensajes: 399 Registrado: 14-August 07 Desde: Temuco Miembro Nº: 8.739 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Problema 4 $TEX: \[<br />\begin{gathered}<br /> x^4 - 6x^2 + 9 = (x + 1)^2 \hfill \\<br /> (x^2 - 3)^2 = (x + 1)^2 /\sqrt . \hfill \\<br /> x^2 - 3 = \pm (x + 1) \hfill \\ <br />\end{gathered} <br />\]$ $TEX: \[<br />\begin{gathered}<br /> x^2 - 3 = + (x + 1) \hfill \\<br /> x^2 - x - 4 = 0 \hfill \\<br /> x = \frac{{1 \pm \sqrt {1 - ( - 16)} }}<br />{2} \hfill \\<br /> x = \frac{{1 \pm \sqrt {17} }}<br />{2} \hfill \\<br /> \boxed{x_1 = \frac{{1 + \sqrt {17} }}<br />{2}} \hfill \\<br /> \boxed{x_2 = \frac{{1 - \sqrt {17} }}<br />{2}} \hfill \\ <br />\end{gathered} <br />\]<br />$ $TEX: \[<br />\begin{gathered}<br /> x^2 - 3 = - (x + 1) \hfill \\<br /> x^2 - x - 2 = 0 \hfill \\<br /> x = \frac{{1 \pm \sqrt {1 - ( - 8)} }}<br />{2} \hfill \\<br /> x = \frac{{1 \pm \sqrt 9 }}<br />{2} \hfill \\<br /> \boxed{x_3 = \frac{{1 + 3}}<br />{2} = 2} \hfill \\<br /> \boxed{x_4 = \frac{{1 - 3}}<br />{2} = - 1} \hfill \\ <br />\end{gathered} <br />\]<br />$ -------------------- Estudiante Ingeniería Civil Matemática - UFRO 09 Ex Alumna Instituto Victoria - IV° A 08

supermantematico Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 11 2008, 11:54 PM Publicado: #4
Principiante Matemático Grupo: Usuario FMAT Mensajes: 3 Registrado: 12-May 07 Desde: Chillán Miembro Nº: 5.804 Nacionalidad: Sexo:	CITA(Versuchung @ Jul 7 2008, 11:01 PM) Problema 4 $TEX: \[<br />\begin{gathered}<br /> x^4 - 6x^2 + 9 = (x + 1)^2 \hfill \\<br /> (x^2 - 3)^2 = (x + 1)^2 /\sqrt . \hfill \\<br /> x^2 - 3 = \pm (x + 1) \hfill \\ <br />\end{gathered} <br />\]$ $TEX: \[<br />\begin{gathered}<br /> x^2 - 3 = + (x + 1) \hfill \\<br /> x^2 - x - 4 = 0 \hfill \\<br /> x = \frac{{1 \pm \sqrt {1 - ( - 16)} }}<br />{2} \hfill \\<br /> x = \frac{{1 \pm \sqrt {17} }}<br />{2} \hfill \\<br /> \boxed{x_1 = \frac{{1 + \sqrt {17} }}<br />{2}} \hfill \\<br /> \boxed{x_2 = \frac{{1 - \sqrt {17} }}<br />{2}} \hfill \\ <br />\end{gathered} <br />\]<br />$ $TEX: \[<br />\begin{gathered}<br /> x^2 - 3 = - (x + 1) \hfill \\<br /> x^2 - x - 2 = 0 \hfill \\<br /> x = \frac{{1 \pm \sqrt {1 - ( - 8)} }}<br />{2} \hfill \\<br /> x = \frac{{1 \pm \sqrt 9 }}<br />{2} \hfill \\<br /> \boxed{x_3 = \frac{{1 + 3}}<br />{2} = 2} \hfill \\<br /> \boxed{x_4 = \frac{{1 - 3}}<br />{2} = - 1} \hfill \\ <br />\end{gathered} <br />\]<br />$ -(x+1)=-x-1 y al pasar a la izquierda te queda: x^2 +x+1=0 y los resultados serían -2 y 1.

Versuchung Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 14 2008, 05:10 PM Publicado: #5
Dios Matemático Grupo: Usuario FMAT Mensajes: 399 Registrado: 14-August 07 Desde: Temuco Miembro Nº: 8.739 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	me había equivocado en las 2 ultimas soluciones quedaría $TEX: \[<br />\begin{gathered}<br /> x^2 - 3 = - (x + 1) \hfill \\<br /> x^2 - 3 = - x - 1 \hfill \\<br /> x^2 + x - 2 = 0 \hfill \\<br /> x = \frac{{ - 1 \pm \sqrt 9 }}<br />{2} \hfill \\<br /> \boxed{x_1 = \frac{{ - 1 + 3}}<br />{2} = 1} \hfill \\<br /> \boxed{x_2 = \frac{{ - 1 - 3}}<br />{2} = - 2} \hfill \\ <br />\end{gathered} <br />\]<br />$ -------------------- Estudiante Ingeniería Civil Matemática - UFRO 09 Ex Alumna Instituto Victoria - IV° A 08

Soul_Hunter Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 15 2008, 05:50 PM Publicado: #6
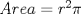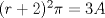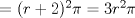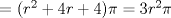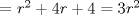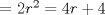Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 665 Registrado: 12-June 07 Desde: the city of the fallen angels Miembro Nº: 6.649 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(House M.D. 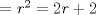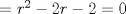@ Jul 15 2008, 03:37 PM) P2 $TEX: $Area = r^2\pi$$ $TEX: $(r + 2)^2\pi = 3A$$ $TEX: = $(r + 2)^2\pi = 3r^2\pi$$ $TEX: = $(r^2 + 4r + 4)\pi = 3r^2\pi$$ $TEX: = $r^2 + 4r + 4 = 3r^2$$ $TEX: = $2r^2 = 4r + 4$$ $TEX: = $r^2 = 2r + 2$$ $TEX: = $r^2 - 2r - 2 = 0$$ Ahora llevamos esto a 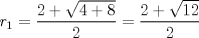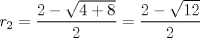$TEX: $r_1 = \dfrac{2 + \sqrt{4 + 8}}{2} = \dfrac{2 + \sqrt{12}}{2}$$ $TEX: $r_2 = \dfrac{2 - \sqrt{4 + 8}}{2} = \dfrac{2 - \sqrt{12}}{2}$$ Recordar que un radio no puede ser negativo, por lo tanto r2 no sirve como solución --------------------

jka_dark28 Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 15 2008, 08:33 PM Publicado: #7
Dios Matemático Grupo: Usuario FMAT Mensajes: 295 Registrado: 3-March 08 Desde: Concepción Miembro Nº: 16.154 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	P4 aquì -------------------- -------------------- Licencias Kaspersky Internet Security 2011 Comerciales para 1 equipo, 1 año. http://www.udec.cl/~juanjtroncoso

Naxoo Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 2 2008, 05:36 PM Publicado: #8
Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	pregunta 5: fg.png ( 6.43k ) Número de descargas: 1 $TEX: \[<br />\begin{gathered}<br /> {\text{En el dibujo los segmentos JE y EI son perpendiculares a AB y AC respectivamente}}{\text{.}} \hfill \\<br /> {\text{Como AE es bisectriz}} \Rightarrow \measuredangle JAE = \measuredangle EAI = \measuredangle IEA = \measuredangle AEJ \Rightarrow JEAI{\text{ es un cuadrado}} \hfill \\<br /> {\text{cuya diagonal es AE}}{\text{, por lo tanto sus lados miden }}\frac{{{\text{35}}\sqrt {\text{2}} }}<br />{{\text{2}}}.{\text{ Notese lo siguiente:}} \hfill \\<br /> \hfill \\<br /> ()EH + HI = \frac{{{\text{35}}\sqrt {\text{2}} }}<br />{{\text{2}}} \wedge AH + HD = 28 \hfill \\<br /> \hfill \\<br /> \vartriangle EDH \sim \vartriangle AIH \Rightarrow \frac{{ED}}<br />{{DH}} = \frac{{AI}}<br />{{IH}} \wedge \frac{{EH}}<br />{{AH}} = \frac{{ED}}<br />{{AI}} \hfill \\<br /> {\text{Por estas proporciones y reemplazando valores se tiene que:}} \hfill \\<br /> \hfill \\<br /> IH = \frac{{{\text{35}}\sqrt {\text{2}} }}<br />{{\text{2}}}k \wedge DH = 21k \hfill \\<br /> AH = \frac{{{\text{35}}\sqrt {\text{2}} }}<br />{{\text{2}}}K \wedge EH = 21K \hfill \\<br /> \hfill \\<br /> {\text{Ahora por () se forma el siguiente sistema de ecuaciones}} \hfill \\ <br />\end{gathered} <br />\]<br />$ $TEX: \[<br />\begin{gathered}<br /> \left. {\underline {\, <br /> \begin{gathered}<br /> 21K + \frac{{{\text{35}}\sqrt {\text{2}} }}<br />{{\text{2}}}k = \frac{{{\text{35}}\sqrt {\text{2}} }}<br />{{\text{2}}} \hfill \\<br /> \frac{{{\text{35}}\sqrt {\text{2}} }}<br />{{\text{2}}}K + 21k = 28 \hfill \\ <br />\end{gathered} \,}}\! \right\| \hfill \\<br /> \hfill \\<br /> {\text{Desarrollando se llega a que }}k = \frac{1}<br />{7} \Rightarrow DH = 3.{\text{ Notemos que }}\vartriangle {\text{EDH}} \sim \vartriangle {\text{ADC}} \Rightarrow \hfill \\<br /> \frac{{{\text{ED}}}}<br />{{{\text{DH}}}} = \frac{{AD}}<br />{{DC}} \Leftrightarrow \frac{{21}}<br />{3} = \frac{{28}}<br />{{DC}} \Leftrightarrow DC = 4 \hfill \\<br /> \hfill \\<br /> {\text{Y por euclides:}} \hfill \\<br /> BD \cdot DC = AD^2 \Leftrightarrow BD \cdot 4 = 28^2 \Leftrightarrow BD = 196 \hfill \\<br /> \hfill \\<br /> \therefore A\vartriangle ABC = \frac{{\left( {BD + DC} \right) \cdot AD}}<br />{2} = \frac{{\left( {196 + 4} \right) \cdot 28}}<br />{2} \Leftrightarrow \boxed{A\vartriangle ABC = 2800} \hfill \\<br /> \hfill \\ <br />\end{gathered} <br />\]<br />$ saludos -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti $TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />$

SanTix Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 2 2008, 07:37 PM Publicado: #9
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 800 Registrado: 13-December 07 Miembro Nº: 13.852 Nacionalidad: Sexo:	otra solución al 5 dp5.PNG ( 3.79k ) Número de descargas: 0 $TEX: \[<br />\begin{gathered}<br /> {\text{por el teo}}{\text{. de euclides:}} \hfill \\<br /> 28^2 = x\left( {y + 21} \right) \Rightarrow \left( {y + 21} \right) = \frac{{28^2 }}<br />{x}{\text{ (1)}} \hfill \\<br /> b^2 = x\left( {x + y + 21} \right) \Rightarrow \left( {x + y + 21} \right) = \frac{{b^2 }}<br />{x}{\text{ (2)}} \hfill \\<br /> c^2 = \left( {y + 21} \right)\left( {x + y + 21} \right){\text{ (3)}} \hfill \\<br /> \hfill \\<br /> {\text{reemplazando (1) y (2) en (3)}} \hfill \\<br /> \frac{{c^2 }}<br />{{b^2 }} = \frac{{28^2 }}<br />{{x^2 }} \Rightarrow \frac{c}<br />{b} = \frac{{28}}<br />{x}{\text{ }}{\text{, pero por el teo}}{\text{. de apolonio tenemos }}\frac{b}<br />{{x + 21}} = \frac{c}<br />{y} \hfill \\<br /> {\text{entonces}}{\text{, }}\frac{{28}}<br />{x} = \frac{y}<br />{{x + 21}} \Rightarrow xy = 28 \cdot \left( {x + 21} \right){\text{, por (1) sabemos que }}xy = 28^2 - 21x \hfill \\<br /> x = 4 \wedge y = 175 \hfill \\<br /> {\text{Area }}\Delta ABC = \frac{{\left( {175 + 21 + 4} \right) \cdot 28}}<br />{2} = 2800 \hfill \\ <br />\end{gathered} <br />\]<br />$

« Posterior · Cuarta Fecha · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 6th March 2025 - 09:41 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.