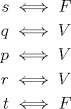Control Recuperativo 2008/1 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad de Chile > Introducción al Álgebra

2 Páginas:

1 2 >

Reply to this topic

Start new topic

Control Recuperativo 2008/1, Hasta Grupos y morfismos

Ictio Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 5 2008, 07:33 PM Publicado: #1
Dios Matemático Grupo: Usuario FMAT Mensajes: 309 Registrado: 28-July 07 Desde: Copiapó-Santiago Miembro Nº: 7.899 Nacionalidad: Universidad: Sexo:	$TEX: \begin{center}<br />\bfseries Control Recuperativo<br />\end{center}<br />Escoja 4 de las siguientes 5 preguntas:\\<br /><br />\noindent \textbf{P1)} Determine los valores de verdad de las proposiciones p, q, r, s, t sabiendo que: $$[(p\Leftrightarrow q) \wedge \overline{(r \Rightarrow s)} \wedge \overline{t}] \Rightarrow [s\vee (q \Rightarrow s)]$$ es falsa.\\<br /><br />\noindent \textbf{P2)} Calcule, adaptándola a una sumatoria telescópica, la siguiente sumatoria $$S=\displaystyle \sum_{k=1}^{n} \dfrac{k\cdot 2^k}{(k+2)!}$$<br /><br />\noindent \textbf{P3)} Considere la sucesión de reales $\{u_n \}_{n\in \mathbb{N}}$ definida por:<br />\begin{equation}<br />\begin{aligned}<br />u_0 &= 2\\<br />u_1 &= 3\\<br />u_n &= 3u_{n-1} -2u_{n-2}<br />\end{aligned}<br />\end{equation}<br />Demuestre que $\forall n \in \mathbb{N},\quad u_n=2^n+1$.\\<br /><br />\noindent \textbf{P4)} Considere el conjunto $A=\{ f:\mathbb{N} \to \mathbb{N} \ \|\ \text{f es función} \}$. Se define en $A$ la relación $\Omega$ por $$f\Omega g \iff f(n) \leq g(n), \qquad \forall n \in \mathbb{N}$$<br />Pruebq eue $\Omega$ es una relación de orden y decida (justificando) si es de orden total o parcial.\\<br /><br />\noindent \textbf{P5)} Sea el conjunto $S=\mathbb{R}\backslash \{-1 \}$. Se define en $S$ la l.c.i $$ como: $$ab=a+b+ab,\qquad \forall a,b \in S$$<br />\begin{enumerate}<br />\item{Sabiendo que $(S,)$ es un grupo abeliano (no lo pruebe), determine el neutro $e \in S$ y el inverso de un elemento $a\in S$ en términos de $a$}<br />\item{Pruebe que $f:(S,)\to (\mathbb{R}\backslash \{0 \},\cdot)$ definida por $$f(x)=x+1$$ es un isomorfismo}<br />\item{Pruebe que $(\mathbb{Q} \backslash \{-1 \},)$ es un subgrupo de $(S,)$}<br />\end{enumerate}$ 1:15 para su resolución motivense pu Saludos. --------------------

Naxoo Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 6 2008, 03:23 PM Publicado: #2
Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Aca va la 2 $TEX: \[<br />\sum\limits_{k = 1}^n {\frac{{k \cdot 2^k }}<br />{{\left( {k + 2} \right)!}}} = \sum\limits_{k = 1}^n {\frac{{\left( {k + 2 - 2} \right) \cdot 2^k }}<br />{{\left( {k + 2} \right)!}} = \sum\limits_{k = 1}^n {\frac{{\left( {k + 2} \right) \cdot 2^k }}<br />{{\left( {k + 2} \right)!}} - \frac{{2 \cdot 2^k }}<br />{{\left( {k + 2} \right)!}}} = \sum\limits_{k = 1}^n {\frac{{2^k }}<br />{{\left( {k + 1} \right)!}} - \frac{{2^{k + 1} }}<br />{{\left( {k + 2} \right)!}}} } <br />\]<br />$ y ahi es clara la suma telescopica -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti $TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />$

"G-ZX" "G-ZX" Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 6 2008, 05:35 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.954 Registrado: 8-March 07 Miembro Nº: 4.393	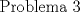$TEX: Problema 3$ Lo demostraremos por inducción: Caso base 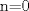$TEX: n=0$ Por lo tanto: 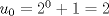$TEX: $u_0 = 2^0 + 1=2$$ Lo cual es verdadero: 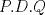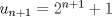$TEX: $P.D.Q$$ $TEX: $ u_{n+1} = 2^{n+1} + 1$$ Usando 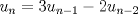$TEX: $u_n = 3u_{n-1} - 2u_{n-2}$$ Podemos deducir que: 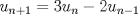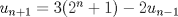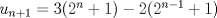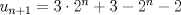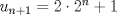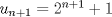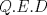$TEX: $u_{n+1}= 3u_n - 2u_{n-1}$$ $TEX: $u_{n+1} = 3(2^n +1) - 2u_{n-1}$$ $TEX: $u_{n+1} = 3(2^n +1) - 2(2^{n-1}+1)$$ $TEX: $u_{n+1} = 3 \cdot 2^{n} + 3 - 2^n -2$$ $TEX: $u_{n+1} = 2\cdot2^n + 1$$ $TEX: $u_{n+1} = 2^{n+1}+1$$ $TEX: $Q.E.D$$ Mensaje modificado por "G-ZX" el Jul 6 2008, 07:54 PM

Ictio Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 6 2008, 06:28 PM Publicado: #4
Dios Matemático Grupo: Usuario FMAT Mensajes: 309 Registrado: 28-July 07 Desde: Copiapó-Santiago Miembro Nº: 7.899 Nacionalidad: Universidad: Sexo:	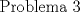CITA("G-ZX @ Jul 6 2008, 06:26 PM) $TEX: Problema 3$ Lo demostraremos por inducción: Caso base 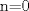$TEX: n=0$ Por lo tanto: 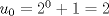$TEX: $u_0 = 2^0 + 1=2$$ Lo cual es verdadero: 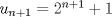$TEX: $P.D.Q$$ $TEX: $ u_{n+1} = 2^{n+1} + 1$$ Usando 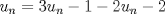$TEX: $u_n = 3u_n-1 - 2u_n-2$$ Podemos deducir que: 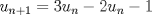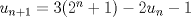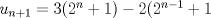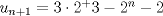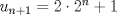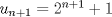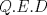$TEX: $u_{n+1}= 3u_n - 2u_n-1$$ $TEX: $u_{n+1} = 3(2^n +1) - 2u_n-1$$ $TEX: $u_{n+1} = 3(2^n +1) - 2(2^{n-1}+1$$ $TEX: $u_{n+1} = 3\cdot2^+ 3 - 2^n -2$$ $TEX: $u_{n+1} = 2\cdot2^n + 1$$ $TEX: $u_{n+1} = 2^{n+1}+1$$ $TEX: $Q.E.D$$ Alguien podría corroborar mi solución ? Correcta la solución aunque tienes demasiados errores de tipeo xD Saludos --------------------

Ictio Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 6 2008, 06:42 PM Publicado: #5
Dios Matemático Grupo: Usuario FMAT Mensajes: 309 Registrado: 28-July 07 Desde: Copiapó-Santiago Miembro Nº: 7.899 Nacionalidad: Universidad: Sexo:	Aquí les dejo mi aporte CITA(Ictio @ Jul 5 2008, 08:23 PM) $TEX: <br />\noindent \textbf{P1)} Determine los valores de verdad de las proposiciones p, q, r, s, t sabiendo que: $$[(p\Leftrightarrow q) \wedge \overline{(r \Rightarrow s)} \wedge \overline{t}] \Rightarrow [s\vee (q \Rightarrow s)]$$ es falsa.$ Es directo del enunciado que: $TEX: <br />\begin{equation}<br />\begin{aligned}<br />\left[ s\vee (q \Rightarrow s) \right] &\iff F\\<br />[s\vee \overline{q} \vee s] &\iff F<br />\end{aligned}<br />\end{equation}<br />De ahí es directo que:\\<br />$s\iff F\\q\iff V$<br />$ $TEX: Además claramente: $$[(p\Leftrightarrow q) \wedge \overline{(r \Rightarrow s)} \wedge \overline{t}] \iff V$$<br />De donde obtenemos que:\\<br />$(p\Leftrightarrow q) \iff V\\<br />¬ (r \Rightarrow s) \iff V\\<br />\overline{t} \iff V$\\<br /><br />Como q era verdadera, concluimos que\\<br />$p\iff V$\\<br />De lo segundo se tiene<br />$$¬ (r \Rightarrow s) \iff ¬(\overline{r} \vee s) \iff ¬(\overline{r} \vee F) \iff \overline{\overline{r}} \iff r \iff V$$ Para concluir, de lo tercero se obtiene que $t\iff F$$ Por tanto nuestros valores son: $TEX: \begin{equation}<br />\begin{aligned}<br />s\iff F\\<br />q\iff V\\<br />p\iff V\\<br />r\iff V\\<br />t\iff F<br />\end{aligned}<br />\end{equation}$ Cualquier error avisen Saludos. Mensaje modificado por Ictio el Jul 6 2008, 06:42 PM --------------------

"G-ZX" "G-ZX" Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 6 2008, 07:49 PM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.954 Registrado: 8-March 07 Miembro Nº: 4.393	CITA(Ictio @ Jul 6 2008, 09:18 PM) Correcta la solución aunque tienes demasiados errores de tipeo xD Saludos Ya está editado ! cualquier error avisar.. Estimado ojalá no se aburra de subir los controles , al sitio , ya que es un gran aporte a la comunidad ! Mensaje modificado por "G-ZX" el Jul 6 2008, 07:50 PM

Rattlehead_ Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 6 2008, 10:22 PM Publicado: #7
Dios Matemático Grupo: Usuario FMAT Mensajes: 428 Registrado: 19-July 07 Desde: Ñuñoa Miembro Nº: 7.679 Nacionalidad: Universidad: Sexo:	CITA(Ictio @ Jul 5 2008, 10:23 PM) $TEX: <br /><br />\noindent \textbf{P5)} Sea el conjunto $S=\mathbb{R}\backslash \{-1 \}$. Se define en $S$ la l.c.i $$ como: $$ab=a+b+ab,\qquad \forall a,b \in S$$<br />\begin{enumerate}<br />\item{Sabiendo que $(S,)$ es un grupo abeliano (no lo pruebe), determine el neutro $e \in S$ y el inverso de un elemento $a\in S$ en términos de $a$}<br />\item{Pruebe que $f:(S,)\to (\mathbb{R}\backslash \{0 \},\cdot)$ definida por $$f(x)=x+1$$ es un isomorfismo}<br />\item{Pruebe que $(\mathbb{Q} \backslash \{-1 \},)$ es un subgrupo de $(S,)$}<br />\end{enumerate}<br />$ $TEX: <br /><br />\noindent 1<br /><br />\noindent Neutro: Demostremos que $0 \in S$ es neutro para operacion , Sean $0,a \in S$<br /><br />$$a0=a+0+a0=a$$<br />$$0a=0+a+0a=a$$<br /><br />\noindent Entonces se cumple que:<br /><br />$$a0=0a=a$$ <br /><br />\noindent $\therefore$ 0 es neutro para operacion en S. \\<br /><br />\noindent Elementos inversos: Sea $a, -a(1+a)^{-1} \in S$ (notar que $-a(1+a)^{-1}$ esta correctamente definido para S, pues $a \in \mathbb{R} - \left\{{-1}\right\} $) \\<br /><br />$$a-a(1+a)^{-1}=a+-a(1+a)^{-1}+a \cdot -a(1+a)^{-1}=0$$<br />$$-a(1+a)^{-1}a=-a(1+a)^{-1}+a+a(1+a)^{-1} \cdot a=0$$ \\<br /><br /><br />\noindent Luego: $a-a(1+a)^{-1}=-a(1+a)^{-1}a=0$ \\<br /><br /><br />\noindent $\therefore$ $-a(1+a)^{-1}$ es neutro de un a cualquiera en S, en terminos de si mismo<br /><br /><br />$ $TEX: <br /><br />\noindent 2 \\<br /><br />\noindent Demostremos primero que es un morfismo, sean $a,b \in S$ <br /><br />$$ f(ab)=f(a+b+ab)=a+b+ab+1=(a+1) \cdot (b+1) = f(a)\cdot f(b)$$<br /><br />\noindent $\therefore f:(S,) \rightarrow (\mathbb{R} - \left\{{-1}\right\}, \cdot )$ es un morfismo \\<br /><br />\noindent Ahora veamos que es un isomorfismo, es decir que f es funcion biyectiva. \\<br /><br />\noindent Inyectividad: Sean $x,y \in S$:<br /><br />$$ f(x)=f(y) \Leftrightarrow x+1=y+1 \Rightarrow x=y$$<br /><br />\noindent Por lo tanto, f es inyectiva. \\<br /><br />\noindent Sobreyectividad: Sea $x=(y-1) \in S$:<br /><br />$$f(x)=y-1+1=y+0=y$$<br /><br />\noindent Hemos encontrado un $x \in S$ que cumple la sobreyectividad, es decir<br /><br /><br />$$\left( {\forall y \in \mathbb{R} - \left\{ { - 1} \right\}} \right)\left( {\exists x \in S} \right)f(x) = y$$ \\<br /><br />\noindent Como f es inyectiva y sobreyectiva, entonces es sobreyectiva \\<br /><br />\noindent $\therefore$ f es isomorfismo<br /><br /><br /><br />$ PD: Despues sigo Mensaje modificado por Metal Militia el Jul 6 2008, 10:42 PM -------------------- "Las Matematicas son el alfabeto con el cual Dios ha escrito el universo"

Ictio Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 6 2008, 10:29 PM Publicado: #8
Dios Matemático Grupo: Usuario FMAT Mensajes: 309 Registrado: 28-July 07 Desde: Copiapó-Santiago Miembro Nº: 7.899 Nacionalidad: Universidad: Sexo:	CITA(Ictio @ Jul 5 2008, 08:23 PM) $TEX: <br />\noindent \textbf{P5)} Sea el conjunto $S=\mathbb{R}\backslash \{-1 \}$. Se define en $S$ la l.c.i $$ como: $$ab=a+b+ab,\qquad \forall a,b \in S$$<br />\begin{enumerate}<br />\item{Sabiendo que $(S,)$ es un grupo abeliano (no lo pruebe), determine el neutro $e \in S$ y el inverso de un elemento $a\in S$ en términos de $a$}<br />\item{Pruebe que $f:(S,)\to (\mathbb{R}\backslash \{0 \},\cdot)$ definida por $$f(x)=x+1$$ es un isomorfismo}<br />\item{Pruebe que $(\mathbb{Q} \backslash \{-1 \},)$ es un subgrupo de $(S,)$}<br />\end{enumerate}$ Motivao. $TEX: \fbox{Solución P5. b}\\<br />Dejaremos al esforzado lector la difícil tarea de comprobar que $f(x)$ es biyectiva\\<br />Resta probar que: $f(xy)=f(x)\cdot f(y)\qquad \forall x,y \in S$<br />\begin{equation}<br />\begin{aligned}<br />f(xy) &= f(x+y+xy)\\<br />&= x+y+xy+1\\<br />&= x+1+y(1+x)\\<br />&= (x+1)(1+y)\\<br />&= f(x)f(y)<br />\end{aligned}<br />\end{equation}<br /><br />Por tanto, $f$ es un isomorfismo$ Así era la cos acierto? xD Mensaje modificado por Ictio el Jul 6 2008, 10:29 PM --------------------

doble_f Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 7 2008, 03:16 PM Publicado: #9
Matemático Grupo: Usuario FMAT Mensajes: 31 Registrado: 14-October 07 Desde: Stgo Miembro Nº: 11.300 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	asi parece y la biyeccion es clara jaja --------------------

andresfh Ver Perfil del Miembro Ver los mensajes de este miembro	May 20 2009, 11:35 PM Publicado: #10
Principiante Matemático Grupo: Usuario FMAT Mensajes: 1 Registrado: 19-May 09 Miembro Nº: 51.716 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA("G-ZX @ Jul 6 2008, 06:35 PM) $TEX: Problema 3$ . . . $TEX: $u_{n+1} = 3(2^n +1) - 2u_{n-1}$$ $TEX: $u_{n+1} = 3(2^n +1) - 2(2^{n-1}+1)$$ en ese paso no se estará usando lo que se quería demostrar?.. ya que la H.I dice que se cumple para algún "n", pero no necesariamente para "n-1"..

« Posterior · Introducción al Álgebra · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 25th April 2025 - 11:52 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.