Triángulo rectángulo conocidísimo

Reglamento Sector de Consultas

Para un correcto uso de este foro debes leer estas reglas:

Este Sector es donde pueden plantear sus dudas de Nivel PSU.
- NO se debe usar el Banco de Problemas Resueltos para consultar.
Hacer UNA CONSULTA por TEMA, ya que asi es mas facil enfocarse solo a la pregunta.
- Si desean hacer varias preguntas, tendran que crear un tema para cada una.
Respecto al TITULO, tratar de ser lo mas claro posible de que trata la consulta.
- Ejemplo de lo que no se debe hacer: "ayuda porfis" ó "Heeeeeelp!"
Después de que el autor del tema haya quedado satisfecho con las respuestas, debera escribir "resuelto" en el título del tema o en la descripción de la discusión.
Usuario que no cumpla estas reglas, sera advertido (en el mismo post o via MP).
- En caso que incurra nuevamente a faltar al reglamento, sera amonestado.

Staff FMAT

Triángulo rectángulo conocidísimo, quizás sea la pregunta que vayas a hacer

_Felipe_ Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 20 2008, 03:36 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.179 Registrado: 4-January 08 Desde: La Florida Miembro Nº: 14.344 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \[<br />\begin{gathered}<br /> En{\text{ }}un{\text{ }}triangulo{\text{ }}ABC{\text{ }}isoceles{\text{ }}rec\tan gulo{\text{ }}en{\text{ }}B,{\text{ }}si{\text{ }}BC = 2{\text{ }}cm{\text{ }}y{\text{ }}O{\text{ }}es{\text{ }}el{\text{ }}centro \hfill \\<br /> del{\text{ }}semicirculo{\text{ }}inscrito,{\text{ }}cuya{\text{ }}area{\text{ }}es. \hfill \\<br /> \hfill \\<br /> A){\text{ }}2\pi \left( {2\sqrt 2 - 2} \right)^2 cm^2 \hfill \\<br /> B){\text{ }}2\pi \left( {2\sqrt 2 + 2} \right)^2 cm^2 \hfill \\<br /> C){\text{ }}2\pi \left( {2\sqrt 3 - 2} \right)^2 cm^2 \hfill \\<br /> D){\text{ }}2\pi \left( {\sqrt 2 + 1} \right)^2 cm^2 \hfill \\<br /> E){\text{ }}2\pi \left( {\sqrt 2 - 1} \right)^2 cm^2 \hfill \\ <br />\end{gathered} <br />\]<br />$

Ussop Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 20 2008, 05:01 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.349 Registrado: 8-October 07 Desde: Quilicura Miembro Nº: 11.057 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	como AC es tangente a la semi circunferencia, OE es perpendicular a AC $TEX: \[<br />\begin{gathered}<br /> \overline {AC} = 2\sqrt 2 \hfill \\<br /> \overline {AE} = \overline {AB} \hfill \\<br /> \overline {AE} = 2 \hfill \\<br /> \overline {EC} = \overline {OE} \hfill \\<br /> \overline {EC} = 2\sqrt 2 - 2 \hfill \\<br /> \overline {OE} = r \hfill \\<br /> \boxed{r = 2\sqrt 2 - 2} \hfill \\<br /> Area = \frac{1}<br />{2}\pi \left( {2\sqrt 2 - 2} \right)^2 \hfill \\<br /> Area = \frac{1}<br />{2}\pi \left( {2\left( {\sqrt 2 - 1} \right)} \right)^2 \hfill \\<br /> Area = \frac{1}<br />{2}\pi \cdot 4\left( {\sqrt 2 - 1} \right)^2 \hfill \\<br /> \boxed{Area = 2\pi \left( {\sqrt 2 - 1} \right)^2 } \hfill \\ <br />\end{gathered} <br />\]$ Archivo(s) Adjunto(s) 2595324913_b1a456161e.jpg ( 8.1k ) Número de descargas: 67 -------------------- Plan Comun Ingenieria USM 2009 Santiago Ingenieria Civil Electrica Usm 2010 Santiago

_Felipe_ Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 20 2008, 05:11 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.179 Registrado: 4-January 08 Desde: La Florida Miembro Nº: 14.344 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	me queda una duda como concluyes que EC=OE

Ussop Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 20 2008, 05:26 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.349 Registrado: 8-October 07 Desde: Quilicura Miembro Nº: 11.057 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	el angulo ACB mide 45º y AO es bisectriz del Angulo CAB nos queda que el triangulo ABO es congruente con el triangulo AEO El triangulo CEO es isosceles rectangulo en E Mensaje modificado por max_734 el Jun 20 2008, 05:30 PM -------------------- Plan Comun Ingenieria USM 2009 Santiago Ingenieria Civil Electrica Usm 2010 Santiago

_Felipe_ Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 20 2008, 05:30 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.179 Registrado: 4-January 08 Desde: La Florida Miembro Nº: 14.344 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(max_734 @ Jun 20 2008, 06:17 PM) el angulo ACB mide 45º y AO es bisectriz del Angulo CAB nos queda que el triangulo ABO es congruente con el triangulo AEO te pasaste =)

Naxoo Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 27 2009, 06:23 PM Publicado: #6
Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Posteare un par de ideas más de solución para que no quede duda, lo esencial es encontrar el radio de la semicircunferencia Definamos a D como el punto de tangencia de la segmento AC 1-. Por áreas: Calcular las áreas, en función del radio, de los triángulos ABO, AOD, y ODC, sumándolas notamos que son igual al área del triángulo ABC 2-. Por poncelet: refljar el triangulo con respecto a BC y notar que se forma un triángulo rectángulo isoceles, y luego aplicamos poncelet, o sea: 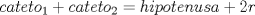$TEX: $cateto_1+cateto_2=hipotenusa+2r$$ donde r es el radio de la circunferencia inscrita al triángulo rectángulo 3_. Por el teorema de la tangente secante: Sea BE diametro de la semicircunferencia, entonces se cumple 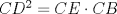$TEX: $CD^2=CE \cdot CB$$ y CE se puede obtener gracias al desarrollo de FelipeAcr Conocía otra solución, pero en estos momentos no la recuerdo, así que están invitados a encontrarla y postearla Espero que les sirva Saludos -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti $TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />$

Link_wnD Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 2 2009, 02:07 PM Publicado: #7
Dios Matemático Grupo: Usuario FMAT Mensajes: 300 Registrado: 23-April 09 Desde: asdasdfa Miembro Nº: 49.234 Nacionalidad: Sexo:	CITA(naxoobkn @ Jun 27 2009, 07:23 PM) Conocía otra solución, pero en estos momentos no la recuerdo, así que están invitados a encontrarla y postearla Espero que les sirva Saludos Con semejanza, si se define E como el punto de tangencia con AC de inmediato salta a la vista 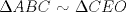$TEX: $·ABC$ $\sim$ $·CEO$$ por lo que $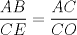TEX: $\dfrac{AB}{CE} = \dfrac{AC}{CO}$$ , de donde se despeja el radio y saludos!

luuchiitoo Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 11 2009, 07:29 PM Publicado: #8
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.832 Registrado: 26-October 07 Desde: concepción Miembro Nº: 11.853 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(naxoobkn @ Jun 27 2009, 07:23 PM) Posteare un par de ideas más de solución para que no quede duda, lo esencial es encontrar el radio de la semicircunferencia Definamos a D como el punto de tangencia de la segmento AC 1-. Por áreas: Calcular las áreas, en función del radio, de los triángulos ABO, AOD, y ODC, sumándolas notamos que son igual al área del triángulo ABC 2-. Por poncelet: refljar el triangulo con respecto a BC y notar que se forma un triángulo rectángulo isoceles, y luego aplicamos poncelet, o sea: $TEX: $cateto_1+cateto_2=hipotenusa+2r$$ donde r es el radio de la circunferencia inscrita al triángulo rectángulo 3_. Por el teorema de la tangente secante: Sea BE diametro de la semicircunferencia, entonces se cumple $TEX: $CD^2=CE \cdot CB$$ y CE se puede obtener gracias al desarrollo de FelipeAcr Conocía otra solución, pero en estos momentos no la recuerdo, así que están invitados a encontrarla y postearla Espero que les sirva Saludos la otra solución es copiar el triangulo para el ladoBC, tal que tengamos un nuevo triangulo isóceles, y sacamos el radio de la circunferencia recordando que: el área del trianguolo es igual al semiperímetro por el inradio. ahí salé facil el área, con los cuidados pertinentes obviamente -------------------- -la inteligencia no es un privilegio, sino un don en benefio de los hermanos... -un gran don conlleva una gran responzabilidad... -un libro puede saber más que un estudiante, pero es mejor el estudiante, ya que el estudiante es capaz de razonar y pensar (fuera de lo espiritual que también es importante)... Paz y Bien...=)

Naxoo Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 12 2009, 10:02 PM Publicado: #9
Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Ya tenemos muchas soluciones al problema Así que si uds ven que otra persona postee esta pregunta, lo asesinan!! xD Saludos P.D: podrían buscarle más soluciones al problema del cuadrado, que también lo marqué como destacado -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti $TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />$

Alonso Metal Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 30 2009, 11:17 PM Publicado: #10
Principiante Matemático Grupo: Usuario FMAT Mensajes: 6 Registrado: 8-August 07 Desde: maipú Miembro Nº: 8.384 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	ese triángulo deberian saberselo de memoría a mi me salio en la PSU de mi generación la del 2006 admisión 2007 la clave es saber tangentes y algo de semejanza de triángulos saludos -------------------- Estudiante de Ingeniería Comercial Universidad de Chile

« Posterior · Consultas de la Semana · Anterior »

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):