|
|
|
|
|
|
|
  |
 Jun 11 2008, 03:26 AM Jun 11 2008, 03:26 AM
Publicado:
#1
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Aca les dejo otro Material de Colección, con problemas muy lindos para cabecearse su buen rato (de mi particular gusto es el Problema 4). Por supuesto deben primero haber pasado por los Materiales que he publicado en los niveles previos.
Que les sea de Gran Provecho para su Entrenamiento, se viene la Clasificacion para la Olimpiada Nacional en unos 2 Meses, asi que hay que ponerle empeño.  Entrenamiento_N_6.pdf ( 33.54k )
Número de descargas: 450
Entrenamiento_N_6.pdf ( 33.54k )
Número de descargas: 450A entrenar -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jun 12 2008, 12:23 AM Jun 12 2008, 12:23 AM
Publicado:
#2
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Ni un agradecimiento
La motivacion para seguir subiendo es que agradezcan y expongan sus soluciones Seguire esperando... Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jun 12 2008, 12:38 AM Jun 12 2008, 12:38 AM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.605 Registrado: 25-June 05 Miembro Nº: 123 Colegio/Liceo:  Universidad:  Sexo:  |
Yo doy las gracias
-------------------- |
|
|
|
 Jun 12 2008, 01:04 AM Jun 12 2008, 01:04 AM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 665 Registrado: 12-June 07 Desde: the city of the fallen angels Miembro Nº: 6.649 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Me sumo a los agradecimientos. Espero algún día tener la habilidad (y el tiempo) para resolverlo...
Salu2 --------------------     |
|
|
|
 Jun 12 2008, 10:34 AM Jun 12 2008, 10:34 AM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
Muchisimas gracias, estan muy bonitos los problemitas (dificiles eso si xD), si sale algo compartire la/s solucion/es. Ademas el PDF esta implecable muy bien presentado
Saludos |
|
|
|
 Jun 12 2008, 02:33 PM Jun 12 2008, 02:33 PM
Publicado:
#6
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 159 Registrado: 7-July 06 Miembro Nº: 1.572 Nacionalidad:  Universidad:  Sexo:  |
Problema 2:
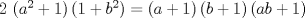 . .Fijamos 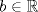 , y resolvemos para , y resolvemos para  donde, donde,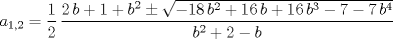 Donde 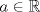 si y solo si si y solo si 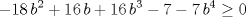 Note que: 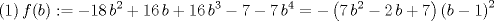 Donde se verifica que 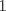 es la única raíz ( doble ) real de la expresión anterior como ecuación para es la única raíz ( doble ) real de la expresión anterior como ecuación para  . .Ahora bien, derivando (1) como función de  , obtenemos , obtenemos  y haciendo y haciendo 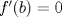 nuevamente 1, es la única raiz real para aquella ecuación. Esto es, 1 es el unico punto critico para (1). nuevamente 1, es la única raiz real para aquella ecuación. Esto es, 1 es el unico punto critico para (1). Luego, 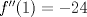 . Así, 1 es un máximo absoluto para . Así, 1 es un máximo absoluto para 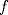 . Evaluando . Evaluando 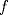 en 1 obtenemos en 1 obtenemos 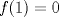 , entonces , entonces 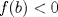 , para , para 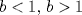 . .Por lo tanto, si  se tiene que se tiene que 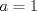 , esto es, el par , esto es, el par 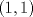 es el único par que satisface la ecuación inicial propuesta. es el único par que satisface la ecuación inicial propuesta.-------------------- ¿El conjunto de todos los conjuntos es un conjunto?  |
|
|
|
 Aug 18 2011, 12:48 PM Aug 18 2011, 12:48 PM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
242 descargas, y app 3 agradecimientos... xD
Gracias. -------------------- Me voy, me jui.
|
|
|
|
 Aug 18 2011, 12:58 PM Aug 18 2011, 12:58 PM
Publicado:
#8
|
|
 Principiante Matemático Grupo: Usuario FMAT Mensajes: 2 Registrado: 29-July 11 Miembro Nº: 92.361 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Graciaaas =)
|
|
|
|
 Nov 28 2011, 05:35 PM Nov 28 2011, 05:35 PM
Publicado:
#9
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 2 Registrado: 27-November 11 Miembro Nº: 97.845 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
gracias
|
|
|
|
 Nov 28 2011, 06:01 PM Nov 28 2011, 06:01 PM
Publicado:
#10
|
|
 Dios Matemático Grupo: Moderador Mensajes: 269 Registrado: 30-August 10 Desde: Santiago, Chile Miembro Nº: 76.269 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Gracias Profesor, se agradece el aporte
Saludos -------------------- Estudiante Instituto Nacional General José Miguel Carrera IV Medio(2013) 17 años. Estaba Jesús predicando en el monte Sinaí y dijo a sus discípulos: y = ax² + bx + c ¿Y eso qué es? Dijo uno de los discípulos. A lo que Jesús respondió: ¡Una parábola !  |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 09:57 PM |










