Entrenamiento Algebra v2.0

Foro fmat.cl > Sector Preparación Olimpiadas > Sector PreOlímpico > Álgebra > Material de Entrenamiento

6 Páginas:

« < 4 5 6

Entrenamiento Algebra v2.0, [Medio]

Opciones

GoChuck Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 29 2009, 06:06 PM Publicado: #51
Dios Matemático Grupo: Usuario FMAT Mensajes: 400 Registrado: 27-October 09 Desde: ¡Qué te importa! Miembro Nº: 61.057 Universidad: Sexo:	Problema 43. Llegué a la solución Bueno.. Partamos por el siguiente hecho.. 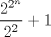$TEX: $\displaystyle \frac{2^{2^n}}{2^2}+1$$ es lo mismo que el enunciado.. Ahora, por el hecho, de que un impar se puede expresar de la forma $TEX: $2x+1$$ Bien, ahora por tanto, según el enunciado, deberíamos tener (recordar que los números primos son todos impartes, por tanto, para satisfacer la necesidad de que sea primo, primero debe ser impar): 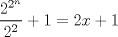$TEX: $\displaystyle \frac{2^{2^n}}{2^2}+1=2x+1$$ Restamos los 1 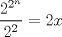$TEX: $\displaystyle \frac{2^{2^n}}{2^2}=2x$$ Multiplicamos por 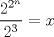$TEX: $\frac{1}{2}$$ $TEX: $\displaystyle \frac{2^{2^n}}{2^3}=x$$ Por tanto 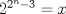$TEX: $2^{{2^n}-3}=x$$ Y sea cual sea el n (mayor que 2), nos daría una potencia de dos, y una potencia de dos es par.. Y es sabido que los primos tienen que ser impares. ! Edit: Damn.. Lo que hice está mal XD.. Sólo me da que el número x es par.. La verdad esque sé que cuando es una potencia de 2, y se le suma 1, tiene que ser divisible por 3, o por 5, pero no tengo ni idea de cómo expresarlo algebraicamente.. Lo dejo como dato por si alguien más quiere hacerlo xD Mensaje modificado por GoChuck el Dec 4 2009, 03:52 PM

Newtype Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 30 2009, 03:37 PM Publicado: #52
Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad: Sexo:	podrian darme un hint para el p 28? -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos

GoChuck Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 30 2009, 04:33 PM Publicado: #53
Dios Matemático Grupo: Usuario FMAT Mensajes: 400 Registrado: 27-October 09 Desde: ¡Qué te importa! Miembro Nº: 61.057 Universidad: Sexo:	... No se me ocurren muchas ideas.. Hasta ahora lo mejor me parecería reducir los números con potencia, a bases primas.. Te saldría más fácil la multiplicación, y también la simplificación.. Pero más que eso, no =/.

El Geek Ver Perfil del Miembro Ver los mensajes de este miembro	May 21 2011, 08:33 AM Publicado: #54
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Está realmente bueno el material. Me gustó que al principio tuviera la fucktorizaciones y luego ejercicios y ejercicios. Excelente, me servirá mucho para ayudar en unos talleres. Saludos. -------------------- Me voy, me jui.

master_c	May 21 2011, 10:19 AM Publicado: #55
Invitado	CITA(Hamon @ Nov 30 2009, 04:37 PM) podrian darme un hint para el p 28? considera $TEX: $x^4 + 4 \cdot 3^4 = \left( {x^2 - 6x + 18} \right)\left( {x^2 + 6x + 18} \right)$$

master_c	May 21 2011, 10:20 AM Publicado: #56
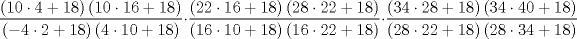Invitado	$TEX: $$<br />\frac{{\left( {10 \cdot 4 + 18} \right)\left( {10 \cdot 16 + 18} \right)}}<br />{{\left( { - 4 \cdot 2 + 18} \right)\left( {4 \cdot 10 + 18} \right)}} \cdot \frac{{\left( {22 \cdot 16 + 18} \right)\left( {28 \cdot 22 + 18} \right)}}<br />{{\left( {16 \cdot 10 + 18} \right)\left( {16 \cdot 22 + 18} \right)}} \cdot \frac{{\left( {34 \cdot 28 + 18} \right)\left( {34 \cdot 40 + 18} \right)}}<br />{{\left( {28 \cdot 22 + 18} \right)\left( {28 \cdot 34 + 18} \right)}}<br />$$$ $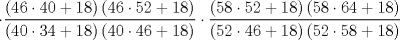TEX: $$<br /> \cdot \frac{{\left( {46 \cdot 40 + 18} \right)\left( {46 \cdot 52 + 18} \right)}}<br />{{\left( {40 \cdot 34 + 18} \right)\left( {40 \cdot 46 + 18} \right)}} \cdot \frac{{\left( {58 \cdot 52 + 18} \right)\left( {58 \cdot 64 + 18} \right)}}<br />{{\left( {52 \cdot 46 + 18} \right)\left( {52 \cdot 58 + 18} \right)}}<br />$$$ $TEX: $$<br /> = \frac{{\left( {58 \cdot 64 + 18} \right)}}<br />{{\left( { - 4 \cdot 2 + 18} \right)}} = \frac{{3730}}<br />{{10}} = 373<br />$$$ Mensaje modificado por master_c el May 21 2011, 10:39 AM

Kreator Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 11 2011, 10:41 PM Publicado: #57
Dios Matemático Grupo: Super Moderador Mensajes: 261 Registrado: 12-February 11 Miembro Nº: 83.790 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Bueno, de partida, estan muy buenos los problemas, he podido hacer varios $TEX: Solución Problema 27<br /><br />Probar que:<br />\[<br />\frac{1}{{\sqrt 1 + \sqrt 2 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }} + \frac{1}{{\sqrt 3 + \sqrt 4 }}... + \frac{1}{{\sqrt {99} + \sqrt {100} }}=S<br />\]<br /><br />Bueno, se puede hacer de varias formas, pero yo lo haré con Sumatorias; entonces, si al enunciado anterior le ponemos S:<br /><br /><br />\[<br />\sum\limits_{n = 1}^{99} {\frac{1}{{\sqrt n + \sqrt {n + 1} }}} = S<br />\]<br /><br />Pero, notamos que:<br />\[<br />1 = n + 1 - n<br />\] De ahí podemos truculentamente factorizar como una suma por su diferencia:<br /><br />\[<br />n + 1 - n = \left( {\sqrt {n + 1} - \sqrt n } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)<br />\]<br /><br />Reemplazando esto en la sumatoria:<br /><br />\[<br />\sum\limits_{n = 1}^{99} {\frac{1}{{\sqrt n + \sqrt {n + 1} }}} = \sum\limits_{n = 1}^{99} {\frac{{\left( {\sqrt {n + 1} - \sqrt n } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)}}{{\sqrt n + \sqrt {n + 1} }}} = \sum\limits_{n = 1}^{99} {\left( {\sqrt {n + 1} - \sqrt n } \right)} <br />\]<br /><br />Entonces, aplicando la propiedad telescópica de las sumatorias:<br /><br />\[<br />\sum\limits_{n = 1}^{99} {\left( {\sqrt {n + 1} - \sqrt n } \right)} = \sqrt {100} - \sqrt 1 = 10 - 1 = 9<br />\]<br /><br />Espero que este bien <img src="style_emoticons/default/smile.gif" style="vertical-align:middle" emoid=":)" border="0" alt="smile.gif" /><br />$ --------------------

Rebo Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 17 2014, 09:41 PM Publicado: #58
Maestro Matemático Grupo: Usuario FMAT Mensajes: 82 Registrado: 22-July 13 Desde: Puerto Montt Miembro Nº: 120.709 Nacionalidad: Sexo:	Algun hint para el P35?

« Posterior · Material de Entrenamiento · Anterior »

6 Páginas:

« < 4 5 6

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 03:19 PM