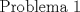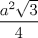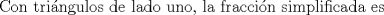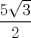|
|
|
|
|
|
|
  |
 Jun 7 2008, 10:29 PM Jun 7 2008, 10:29 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 665 Registrado: 12-June 07 Desde: the city of the fallen angels Miembro Nº: 6.649 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
--------------------     |
|
|
|
 Jun 8 2008, 01:13 AM Jun 8 2008, 01:13 AM
Publicado:
#2
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
-------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jun 8 2008, 07:18 PM Jun 8 2008, 07:18 PM
Publicado:
#3
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 75 Registrado: 10-May 07 Desde: Los Angeles - Chile Miembro Nº: 5.744 Nacionalidad:  Colegio/Liceo:  Sexo:  |
hola... ayer en una fiesta estaba pensando este problema i no se me ocurria xD!!!
y no soi de este nivel pro un amio me dijo este problema i io dije ooo q bkn deve aver una forma.. pro era imposible hacerlo xD emmm... segun lo que creo.. todos los numeros naturlaes tienen una factorizacion prima...i la combinacion de multiplicaciones ntre esos numeros de las factorizaciones primas.. son los determinados N... si esos 66666..n veces estan hechos por una factorizacion prima determinada tal que se puedan formar todos los numeros.... cuando el numero ya s mui grande.. la factorizacion prima va creciendo... osea que el nuero cada vez va teniendo nuevos valores en la factorizacion prima... entonces mas combinaciones de numeros se pueden hacer.... como los numeros primos son los problematicos... ya que ellos mismo son los primos.. pudiera se que estos numeros primos vallan saliendo en ese numero a medida que el numero va creciendo.. ya que los numeros no primos creo q no son mucho problema ya que se pueden hacer de diversas combinaciones de numeros primos... ? Mensaje modificado por Zeok el Jun 8 2008, 07:29 PM |
|
|
|
 Jun 8 2008, 08:44 PM Jun 8 2008, 08:44 PM
Publicado:
#4
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 122 Registrado: 6-October 06 Desde: VIII Región Miembro Nº: 2.438 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
|
|
|
|
 Jun 8 2008, 10:37 PM Jun 8 2008, 10:37 PM
Publicado:
#5
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 264 Registrado: 11-January 08 Desde: Concepcion Miembro Nº: 14.558 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
   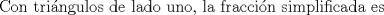 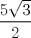
Razón de edición: Te edite los errores del Latex (debes poner solo un $ al principio y otro al final)
Archivo(s) Adjunto(s)
|
|
|
|
 Jun 8 2008, 10:55 PM Jun 8 2008, 10:55 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 665 Registrado: 12-June 07 Desde: the city of the fallen angels Miembro Nº: 6.649 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
--------------------     |
|
|
|
 Jun 9 2008, 12:19 AM Jun 9 2008, 12:19 AM
Publicado:
#7
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
hola... ayer en una fiesta estaba pensando este problema i no se me ocurria xD!!! y no soi de este nivel pro un amio me dijo este problema i io dije ooo q bkn deve aver una forma.. pro era imposible hacerlo xD emmm... segun lo que creo.. todos los numeros naturlaes tienen una factorizacion prima...i la combinacion de multiplicaciones ntre esos numeros de las factorizaciones primas.. son los determinados N... si esos 66666..n veces estan hechos por una factorizacion prima determinada tal que se puedan formar todos los numeros.... cuando el numero ya s mui grande.. la factorizacion prima va creciendo... osea que el nuero cada vez va teniendo nuevos valores en la factorizacion prima... entonces mas combinaciones de numeros se pueden hacer.... como los numeros primos son los problematicos... ya que ellos mismo son los primos.. pudiera se que estos numeros primos vallan saliendo en ese numero a medida que el numero va creciendo.. ya que los numeros no primos creo q no son mucho problema ya que se pueden hacer de diversas combinaciones de numeros primos... ? El problema es ¿Porque aparecen todos los primos posibles en sus factorizaciones primas? ¿Y si se salta alguno? ¿Y si no siguieran creciendo los primos que intervienen? No basta con que los números crezcan. De hecho, si la secuencia fuera otra, por ejemplo 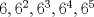 ,etc... estos valores van creciendo, pero en sus factorizaciones primas solo se usan el 2 y el 3. ,etc... estos valores van creciendo, pero en sus factorizaciones primas solo se usan el 2 y el 3.Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jun 9 2008, 03:34 PM Jun 9 2008, 03:34 PM
Publicado:
#8
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 75 Registrado: 10-May 07 Desde: Los Angeles - Chile Miembro Nº: 5.744 Nacionalidad:  Colegio/Liceo:  Sexo:  |
hola... emmm no se si el señor kenshin dejo esta solución como un gran hint o dejo la respuesta abierta para que podamos ver el porque =) ... o tal vez esa es la solucion y no hay que ver el porque y toi dando jugo xD
bueno emm... hay muuuchos numeros de la forma 6666.... ( N ) y si encontramos ese tal N es divisible por alguno de esos ya lo encontramos... pero si no al ser los restos de la forma ( 1, 2, 3 ....... N - 1 ) por lo tanto dentro de los N numeros hay 2 que tienen el mismo resto al ser divididos por n... creo que se llama palomar.... entonces tenemos 2 numeros de la forma 6666.... que dejan el mismo resto al dividir por n pero.. porque si se restan son divisibles por n??? creo que es prque si tenemos un numero que es congruente a ese resto modulo n y tenemos otro numero que es congruente al mismo resto modulo n... si los restamos quedaria congruente a 0 modulo n y seria divisible por n.... ahora ese numero nos sirve porque la resta va a ser de la forma 666....6000.....0 ya que si tenemos dos numeros ejemplo 666666-6666 = 660000 ya que se van restando la unidad con la unidad decena con decena centena con centena etc entoces quedara de la forma 666.....6000...0 por lo tanto si existe ese numero que al ser multiplicado por el numero natural nos de un numero hecho de puros 6's o 0's y 6's =) Mensaje modificado por Zeok el Jun 9 2008, 04:57 PM |
|
|
|
 Jun 9 2008, 03:50 PM Jun 9 2008, 03:50 PM
Publicado:
#9
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
Kenshin ya dio la solucion al P3, ahora quizas tu la dejaste mas clara xD (por lo menos yo entendi las dos soluciones). Aqui hay un problema que se resuelve con la misma idea.
Saludos |
|
|
|
 Jun 9 2008, 04:09 PM Jun 9 2008, 04:09 PM
Publicado:
#10
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 75 Registrado: 10-May 07 Desde: Los Angeles - Chile Miembro Nº: 5.744 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Kenshin ya dio la solucion al P3, ahora quizas tu la dejaste mas clara xD (por lo menos yo entendi las dos soluciones). Aqui hay un problema que se resuelve con la misma idea. Saludos ucha creia que el señor kenshin la avia dejado abierta pq avian unas preguntas asi " porque? " tonc crei que habia que responderlas nosotros.. |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 02:53 PM |





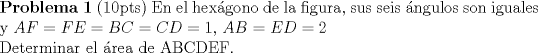

![TEX: <br />\noindent \textbf{Problema 2} (10pts) Considerar un $\triangle ABC$ con $\measuredangle ACB = \measuredangle ABD$, donde D es un punto en el lado AC tal que $AD=4$ y $DC=5$. Determinar la longitud de AB\\[5mm] \textbf{Problema 3} (10pts) Se tiene que $7 \times 858=6006$ y $12 \times 5 =60$. Demostrar que para cualquier número entero positivo N, existe un número entero positivo m tal que el producto $N \times m$ se escribe sólo con dígitos 6 y 0.](./tex/e0b420ae38078f0dd7693a29d0acb5dd.png)






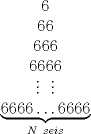
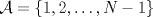 , por lo cual hay dos de ellos que tienen el mismo resto al ser divididos por N. La resta de estos dos números sera divisible por N (¿Porque?).
, por lo cual hay dos de ellos que tienen el mismo resto al ser divididos por N. La resta de estos dos números sera divisible por N (¿Porque?).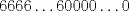 , o sea un número compuesto con sólo seis y ceros. (¿Porque?)
, o sea un número compuesto con sólo seis y ceros. (¿Porque?)

![TEX: <br />\[<br />\begin{array}{l}<br /> {\rm Tenemos\ los\ }\Delta BGA,\ {\rm }\Delta GFA,\ {\rm }\Delta CDH{\rm\ y\ }\Delta DEH{\rm\ que\ son\ congruentes\ por} \\ <br /> {\rm criterio\ A}{\rm .L}{\rm .A}{\rm .\ Ademas\ estos\ triangulos\ son\ 30 - 60 - 90}{\rm .\ Por\ lo\ que\ }\overline {{\rm AG}} = \frac{1}{2}{\rm\ y } \\ <br /> \overline {{\rm BG}} = \frac{{\sqrt 3 }}{2}.{\rm Luego }\left( {{\rm BGA}} \right) = \frac{{\sqrt 3 }}{8}{\rm\ y\ }\left( {{\rm BCHG}} \right) = \sqrt 3 \\ <br /> \left( {ABCDEF} \right) = 4\cdot\frac{{\sqrt 3 }}{8} + \sqrt 3 = \frac{{5\sqrt 3 }}{2} \\ <br /> \end{array}<br />\]<br />](./tex/011a544ade78beb12d6e7fb9467d8a7a.png)