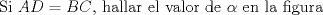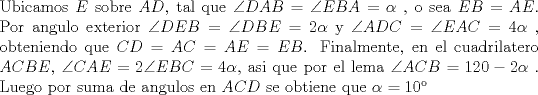Maraton Preolímpica - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Sector PreOlímpico > Otros > Problemas Propuestos

5 Páginas:

« < 2 3 4 5 >

Closed Topic

Start new topic

Maraton Preolímpica, A Resolver!!!

CyedqD Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 20 2008, 09:41 PM Publicado: #31
Coordinador General Gran Maraton PSU Final 2008 Grupo: Moderador Mensajes: 1.607 Registrado: 11-June 07 Desde: Peñalolen, Stgo Miembro Nº: 6.641 Nacionalidad: Universidad: Sexo:	$TEX: Si $AD=BC$, hallar el valor de $\alpha$ en la figura$ 2e.PNG ( 8.62k ) Número de descargas: 1 --------------------

pelao_malo Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 20 2008, 11:27 PM Publicado: #32
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: \noindent Sea $P\in{BD}$ tal que $CD=DP$. Como $\angle BDC=180-4x\Rightarrow \angle DCP=\angle DPC=2x\Rightarrow BP=CP=AD=AB$. Copiamos el $\triangle ABD$ sobre el lado $AC$ tal que $A\to X$. Por la transformaci\'on tenemos $AD=XC=AX=AB$, $\angle XAD=4x$ por lo tanto $PD\|\|XA$ y como $XD=AP$ tenemos que $AXDP$ es un trapecio is\'osceles, por lo tanto $PX=AD$ (diagonales iguales) y de eso y se deduce que $PX=XC=CP$ por lo tanto $\triangle XPC$ es equil\'atero. Pero como $AX=XC$ tenemos $\angle DCX=4x$ entonces $\angle PCX=60=6x\Rightarrow x=10$.$ salu2 -------------------- $TEX: $\sqrt{5}=41$$

CyedqD Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 21 2008, 12:43 AM Publicado: #33
Coordinador General Gran Maraton PSU Final 2008 Grupo: Moderador Mensajes: 1.607 Registrado: 11-June 07 Desde: Peñalolen, Stgo Miembro Nº: 6.641 Nacionalidad: Universidad: Sexo:	CITA(pelao_malo @ Jun 21 2008, 12:18 AM) $TEX: \noindent Sea $P\in{BD}$ tal que $CD=DP$. Como $\angle BDC=180-4x\Rightarrow \angle DCP=\angle DPC=2x\Rightarrow BP=CP=AD=AB$. Copiamos el $\triangle ABD$ sobre el lado $AC$ tal que $A\to X$. Por la transformaci\'on tenemos $AD=XC=AX=AB$, $\angle XAD=4x$ por lo tanto $PD\|\|XA$ y como $XD=AP$ tenemos que $AXDP$ es un trapecio is\'osceles, por lo tanto $PX=AD$ (diagonales iguales) y de eso y se deduce que $PX=XC=CP$ por lo tanto $\triangle XPC$ es equil\'atero. Pero como $AX=XC$ tenemos $\angle DCX=4x$ entonces $\angle PCX=60=6x\Rightarrow x=10$.$ salu2 bonita solucion, la mia: Lema: ( el segundo) En el problema asdweee.PNG ( 16.32k ) Número de descargas: 0 $TEX: \noindent Ubicamos $E$ sobre $AD$, tal que $\angle DAB = \angle EBA = \alpha$ , o sea $EB=AE$. Por angulo exterior $\angle DEB = \angle DBE = 2\alpha$ y $\angle ADC =\angle EAC = 4\alpha$ , obteniendo que $CD = AC = AE = EB$. Finalmente, en el cuadrilatero $ACBE$, $\angle CAE = 2 \angle EBC = 4\alpha$, asi que por el lema $\angle ACB = 120 - 2\alpha$ . Luego por suma de angulos en $ACD$ se obtiene que $\alpha = 10º$$ --------------------

pelao_malo Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 21 2008, 01:25 AM Publicado: #34
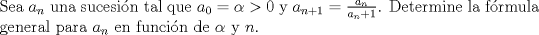
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: \noindent Sea $a_n$ una sucesi\'on tal que $a_0=\alpha>0$ y $a_{n+1}=\frac{a_n}{a_n+1}$. Determine la f\'ormula general para $a_n$ en funci\'on de $\alpha$ y $n$.$ -------------------- $TEX: $\sqrt{5}=41$$

caf_tito Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 21 2008, 12:02 PM Publicado: #35
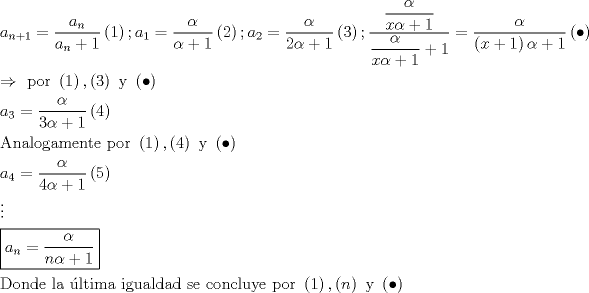
Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.605 Registrado: 25-June 05 Miembro Nº: 123 Colegio/Liceo: Universidad: Sexo:	$TEX: $\begin{gathered}<br /> a_{n + 1} = \frac{{a_n }}<br />{{a_n + 1}}\left( 1 \right);a_1 = \dfrac{\alpha }<br />{{\alpha + 1}}\left( 2 \right);a_2 = \dfrac{\alpha }<br />{{2\alpha + 1}}\left( 3 \right);\dfrac{{\dfrac{\alpha }<br />{{x\alpha + 1}}}}<br />{{\dfrac{\alpha }<br />{{x\alpha + 1}} + 1}} = \dfrac{\alpha }<br />{{\left( {x + 1} \right)\alpha + 1}}\left( \bullet \right) \hfill \\<br /> \Rightarrow {\text{ por }}\left( 1 \right),\left( 3 \right){\text{ y }}\left( \bullet \right) \hfill \\<br /> a_3 = \frac{\alpha }<br />{{3\alpha + 1}}\left( 4 \right) \hfill \\<br /> {\text{Analogamente por }}\left( 1 \right),\left( 4 \right){\text{ y }}\left( \bullet \right) \hfill \\<br /> a_4 = \frac{\alpha }<br />{{4\alpha + 1}}\left( 5 \right) \hfill \\<br /> \vdots \hfill \\<br /> \boxed{a_n = \frac{\alpha }<br />{{n\alpha + 1}}} \hfill \\<br /> {\text{Donde la última igualdad se concluye por }}\left( 1 \right),\left( n \right){\text{ y }}\left( \bullet \right) \hfill \\ <br />\end{gathered}$$ --------------------

pelao_malo Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 21 2008, 02:12 PM Publicado: #36
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad: Colegio/Liceo: Sexo:	Respuesta correcta por caf master mi solucion $TEX: \noindent Probaremos que la f\'ormula es $a_n=\frac{\alpha}{n\alpha+1}$ por inducci\'on.\\<br />El caso $n=0$ es el enunciado, as\'i que podemos asumir que existe un $k\in\mathbb{N}$ tal que $a_k=\frac{\alpha}{k\alpha+1}$. Entonces tenemos $$a_{k+1}=\frac{a_k}{a_k+1}=\dfrac{\frac{\alpha}{k\alpha+1}}{\frac{\alpha}{k\alpha+1}+1}=\frac{\alpha}{(k+1)\alpha+1}\ \ \ \blacksquare$$$ -------------------- $TEX: $\sqrt{5}=41$$

caf_tito Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 21 2008, 05:14 PM Publicado: #37
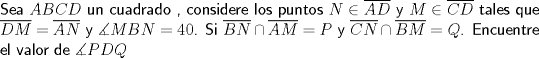Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.605 Registrado: 25-June 05 Miembro Nº: 123 Colegio/Liceo: Universidad: Sexo:	$TEX: \noindent \textsf{Sea $ABCD$ un cuadrado , considere los puntos $N \in \overline{AD}$ y $M \in \overline{CD}$ tales que $\overline{DM}=\overline{AN}$ y $\measuredangle MBN=40$. Si $\overline{BN} \cap \overline{AM}=P$ y $\overline{CN} \cap \overline{BM}=Q$. Encuentre el valor de $\measuredangle PDQ$}$ --------------------

pelao_malo Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 21 2008, 05:37 PM Publicado: #38
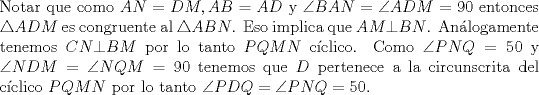
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: \noindent Notar que como $AN=DM,AB=AD$ y $\angle BAN=\angle ADM=90$ entonces $\triangle ADM$ es congruente al $\triangle ABN$. Eso implica que $AM\bot BN$. An\'alogamente tenemos $CN\bot BM$ por lo tanto $PQMN$ c\'iclico. Como $\angle PNQ=50$ y $\angle NDM=\angle NQM=90$ tenemos que $D$ pertenece a la circunscrita del c\'iclico $PQMN$ por lo tanto $\angle PDQ=\angle PNQ=50$.$ -------------------- $TEX: $\sqrt{5}=41$$

caf_tito Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 21 2008, 05:44 PM Publicado: #39
Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.605 Registrado: 25-June 05 Miembro Nº: 123 Colegio/Liceo: Universidad: Sexo:	Excelente Sr pelao_malo era exactamente la solución que esperaba. --------------------

pelao_malo Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 21 2008, 05:47 PM Publicado: #40
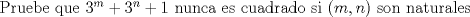Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: \noindent Pruebe que $3^m+3^n+1$ nunca es cuadrado si $(m,n)$ son naturales$ -------------------- $TEX: $\sqrt{5}=41$$

« Posterior · Problemas Propuestos · Anterior »

5 Páginas:

« < 2 3 4 5 >

Closed Topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Versión Lo-Fi

Fecha y Hora actual: 9th April 2025 - 07:12 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.