|
|
|
|
|
|
|
  |
 Jun 8 2008, 08:23 PM Jun 8 2008, 08:23 PM
Publicado:
#11
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
No se si esta bien, pero lo que hice fue lo siguiente: ![TEX: \[<br />\begin{gathered}<br /> x^2 + (x + 1)^2 = y^2 \hfill \\<br /> x^2 + x^2 + 2x + 1 = y^2 \hfill \\<br /> 2x^2 + 2x + 1 = y^2 \hfill \\<br /> {\text{De este podemos decir que }}a = 2,b = 2 \wedge c = 1,{\text{luego}} \hfill \\<br /> \frac{{ - b \pm \sqrt {b^2 - 4ac} }}<br />{{2a}} \to \frac{{ - 2 \pm \sqrt {2^2 - 4 \bullet 2 \bullet 1} }}<br />{{2 \bullet 2}} \hfill \\<br /> \frac{{ - 2 \pm \sqrt {4 - 8} }}<br />{4} = \frac{{ - 2 \pm \sqrt { - 4} }}<br />{4} \hfill \\ <br />\end{gathered} <br />\]](./tex/9515062aeffd75f78818d98708d3435d.png) Llego hasta ahi, pero luego de esa raiz, en el numerador me pierdo. Si alguien me puede ayudar. Saludos Lo que tu tratas de hacer aqui es despejar a x, fijate que la formula que tu ocupas para despejar x es en la ecuacion 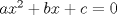 , pero aqui el lado derecho es , pero aqui el lado derecho es 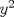 (no siempre es 0). Tu idea es sacar x, pero fijate que te piden demostrar que la ecuacion tiene infinitas soluciones, asi que yo no haria lo que tu estas haciendo, porlomenos (esa formula es muy psu xD, yo no haria eso). Cuidado que si una ecuacion tiene infinitas soluciones, no quiere decir que siempre tenga soluciones. (no siempre es 0). Tu idea es sacar x, pero fijate que te piden demostrar que la ecuacion tiene infinitas soluciones, asi que yo no haria lo que tu estas haciendo, porlomenos (esa formula es muy psu xD, yo no haria eso). Cuidado que si una ecuacion tiene infinitas soluciones, no quiere decir que siempre tenga soluciones.Saludos |
|
|
|
 Jun 8 2008, 09:37 PM Jun 8 2008, 09:37 PM
Publicado:
#12
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 817 Registrado: 28-May 06 Desde: maipú, santiago. Miembro Nº: 1.210 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
No se si esta bien, pero lo que hice fue lo siguiente: ![TEX: \[<br />\begin{gathered}<br /> x^2 + (x + 1)^2 = y^2 \hfill \\<br /> x^2 + x^2 + 2x + 1 = y^2 \hfill \\<br /> 2x^2 + 2x + 1 = y^2 \hfill \\<br /> {\text{De este podemos decir que }}a = 2,b = 2 \wedge c = 1,{\text{luego}} \hfill \\<br /> \frac{{ - b \pm \sqrt {b^2 - 4ac} }}<br />{{2a}} \to \frac{{ - 2 \pm \sqrt {2^2 - 4 \bullet 2 \bullet 1} }}<br />{{2 \bullet 2}} \hfill \\<br /> \frac{{ - 2 \pm \sqrt {4 - 8} }}<br />{4} = \frac{{ - 2 \pm \sqrt { - 4} }}<br />{4} \hfill \\ <br />\end{gathered} <br />\]](./tex/9515062aeffd75f78818d98708d3435d.png) Llego hasta ahi, pero luego de esa raiz, en el numerador me pierdo. Si alguien me puede ayudar. Saludos Lo que tu tratas de hacer aqui es despejar a x, fijate que la formula que tu ocupas para despejar x es en la ecuacion 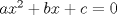 , pero aqui el lado derecho es , pero aqui el lado derecho es 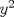 (no siempre es 0). Tu idea es sacar x, pero fijate que te piden demostrar que la ecuacion tiene infinitas soluciones, asi que yo no haria lo que tu estas haciendo, porlomenos (esa formula es muy psu xD, yo no haria eso). Cuidado que si una ecuacion tiene infinitas soluciones, no quiere decir que siempre tenga soluciones. (no siempre es 0). Tu idea es sacar x, pero fijate que te piden demostrar que la ecuacion tiene infinitas soluciones, asi que yo no haria lo que tu estas haciendo, porlomenos (esa formula es muy psu xD, yo no haria eso). Cuidado que si una ecuacion tiene infinitas soluciones, no quiere decir que siempre tenga soluciones.Saludos El método que usa 69___ permite llegar a una solución (lo que es prueba de que es un problema que no requiere muchos conocimientos), aunque quizá no sea la única forma de hacerlo. El dilema es que no se está aplicando la fórmula de la cuadrática correctamente, pues como dice felipe el lado derecho es 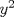 . Sin embargo esto tiene un arreglo bastante fácil, y es que dejar un cero al lado derecho es simplemente una cuestión algebraica. Luego sólo basta establecer ciertas condiciones necesarias y el problema sale solito. . Sin embargo esto tiene un arreglo bastante fácil, y es que dejar un cero al lado derecho es simplemente una cuestión algebraica. Luego sólo basta establecer ciertas condiciones necesarias y el problema sale solito.Edito: rectifico pues al formar la sucesión de soluciones no me percate de que era periódica, y por tanto no sirve. Sin embargo, era una buena forma de empezar a afrontar el problema. -------------------- Estudiante de 5º año de Ingeniería Civil Industrial en la U. de Chile
|
|
|
|
 Jun 9 2008, 03:20 AM Jun 9 2008, 03:20 AM
Publicado:
#13
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Yo creo que al menos como yo la estoy viendo, al menos requiere manejarse un poco con Ecuaciones de Pell.
Esto pues la Ecuación se puede escribir como  Como ya es sabido, la ecuaciones de Pell 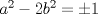 tienen infinitas soluciones tienen infinitas soluciones 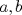 enteras (de hecho son las mas clásicas), y no es dificil notar que "a" debe ser impar, por lo que se puede hacer una relacion directa entre las soluciones de una y otra ecuación. enteras (de hecho son las mas clásicas), y no es dificil notar que "a" debe ser impar, por lo que se puede hacer una relacion directa entre las soluciones de una y otra ecuación.No creo que sea tan simple el propuesto para Nivel Preolimpico (ojala haya una solución mas agradable que no use Pell) Saludos PD: Lamentablemente para el que no sabe del tema, probablemente lo que escribi recien es chino Por eso dejo unos links para los que sepan Ingles http://mathworld.wolfram.com/PellEquation.html PD: Ademas le agregue un adjunto  Ecuaci_n_de_Pell.pdf ( 106.77k )
Número de descargas: 87
Ecuaci_n_de_Pell.pdf ( 106.77k )
Número de descargas: 87PD: Y los que quieran calcular una Solucion Fundamental para la Ecuación de Pell http://frontend.bioinfo.rpi.edu/zukerm/cgi-bin/dq.html -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jun 9 2008, 11:37 AM Jun 9 2008, 11:37 AM
Publicado:
#14
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad:  Colegio/Liceo:  Sexo:  |
yo lo hice de la misma manera jjajajaja
me parece que pell es como muy directo aqui pero pense que iba a ver otra solucion xD asi que kenshin, postee el siguiente propuesto --------------------  |
|
|
|
 Jun 10 2008, 04:34 PM Jun 10 2008, 04:34 PM
Publicado:
#15
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Dado que Kenshin esta muy ocupado, postearé yo el siguiente problema
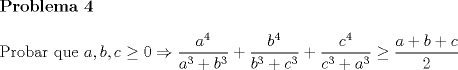 salu2 --------------------  |
|
|
|
 Jun 10 2008, 09:34 PM Jun 10 2008, 09:34 PM
Publicado:
#16
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Dado que Kenshin esta muy ocupado, postearé yo el siguiente problema 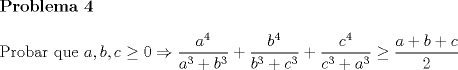 salu2 La condicion deberia ser 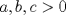 o algo que impida que los denominadores puedan ser cero. Una sutileza pero vale la pena hacer el alcance. Por cierto se puede usar una tecnica aprendida en "Tecnicas de Resolución de Problemas" este Verano ^^ o algo que impida que los denominadores puedan ser cero. Una sutileza pero vale la pena hacer el alcance. Por cierto se puede usar una tecnica aprendida en "Tecnicas de Resolución de Problemas" este Verano ^^Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jun 11 2008, 08:18 PM Jun 11 2008, 08:18 PM
Publicado:
#17
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.429 Registrado: 6-October 07 Miembro Nº: 10.987 |
Intente realizarla, y no me convence mucho, asi que para que me la corrijan.
![TEX: \[<br />\begin{gathered}<br /> \Pr imero{\text{ }}que{\text{ }}todo,{\text{ }}probare{\text{ }}que \hfill \\<br /> a,b,c \geqslant 0 \hfill \\<br /> a,b,c \geqslant 0/()^n \hfill \\<br /> a^n ,b^n ,c^n \geqslant 0^n \hfill \\<br /> a^n ,b^n ,c^n \geqslant 0 \hfill \\<br /> \Rightarrow \boxed{a,b,c \geqslant 0} \hfill \\<br /> Ahora,la{\text{ }}2da{\text{ }}desigualdad. \hfill \\<br /> \frac{{a^4 }}<br />{{a^3 + b^3 }} + \frac{{b^4 }}<br />{{b^3 + c^3 }} + \frac{{c^4 }}<br />{{c^3 + a^3 }} \geqslant \frac{{a + b + c}}<br />{2} \hfill \\<br /> \frac{{a^4 }}<br />{{a^3 + b^3 }} + \frac{{b^4 }}<br />{{b^3 + c^3 }} + \frac{{c^4 }}<br />{{c^3 + a^3 }} \geqslant \frac{{a + b + c}}<br />{2}/ \bullet 2 \hfill \\<br /> \frac{{2a^4 }}<br />{{2a^3 + 2b^3 }} + \frac{{2b^4 }}<br />{{2b^3 + 2c^3 }} + \frac{{2c^4 }}<br />{{2c^3 + 2a^3 }} \geqslant \frac{{2a + 2b + 2c}}<br />{{2 \bullet 2}} \hfill \\<br /> \frac{{2a^4 }}<br />{{2(a^3 + b^3 )}} + \frac{{2b^4 }}<br />{{2(b^3 + c^3 )}} + \frac{{2c^4 }}<br />{{2(c^3 + a^3 )}} \geqslant \frac{{2(a + b + c)}}<br />{4}/:2 \hfill \\<br /> \Rightarrow \boxed{\frac{{a^4 }}<br />{{a^3 + b^3 }} + \frac{{b^4 }}<br />{{b^3 + c^3 }} + \frac{{c^4 }}<br />{{c^3 + a^3 }} \geqslant \frac{{a + b + c}}<br />{2}}\blacktriangle \hfill \\ <br />\end{gathered} <br />\]](./tex/ad9adbf9a1f9afe9dbf5bdad9033e87b.png) Me imagino que ![TEX: \[<br />a,b,c \in \mathbb{R}<br />\]](./tex/94ca7e8d70e8397ef4e9dbb80bfc1a10.png) No me tengo mucha fe, pero igual. Saludos Edit:Me equivoque de puro....en una estupida suma.xD Mensaje modificado por 69___ el Jun 11 2008, 08:42 PM -------------------- CHAO.
|
|
|
|
 Jun 11 2008, 08:45 PM Jun 11 2008, 08:45 PM
Publicado:
#18
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
Intente realizarla, y no me convence mucho, asi que para que me la corrijan. ![TEX: \[<br />\begin{gathered}<br /> \Pr imero{\text{ }}que{\text{ }}todo,{\text{ }}probare{\text{ }}que{\text{ }} \hfill \\<br /> a,b,c \geqslant 0/()^n \hfill \\<br /> a^n ,b^n ,c^n \geqslant 0^n \hfill \\<br /> a^n ,b^n ,c^n \geqslant 0 \hfill \\<br /> \Rightarrow \boxed{a,b,c \geqslant 0} \hfill \\<br /> Ahora,probare{\text{ }}que \hfill \\<br /> \frac{{a^4 }}<br />{{a^3 + b^3 }} + \frac{{b^4 }}<br />{{b^3 + c^3 }} + \frac{{c^4 }}<br />{{c^3 + a^3 }} \geqslant \frac{{a + b + c}}<br />{2}/ \bullet 2 \hfill \\<br /> \frac{{2a^4 }}<br />{{2a^3 + 2b^3 }} + \frac{{2b^4 }}<br />{{2b^3 + 2c^3 }} + \frac{{2c^4 }}<br />{{2c^3 + 2a^3 }} \geqslant \frac{{2a + 2b + 2c}}<br />{{2 \bullet 2}} \hfill \\<br /> \frac{{2a^4 }}<br />{{2(a^3 + b^3 )}} + \frac{{2b^4 }}<br />{{2(b^3 + c^3 )}} + \frac{{2c^4 }}<br />{{2(c^3 + a^3 )}} \geqslant \frac{{2(a + b + c)}}<br />{4}/:2 \hfill \\<br /> \frac{{a^4 }}<br />{{a^3 + b^3 }} + \frac{{b^4 }}<br />{{b^3 + c^3 }} + \frac{{c^4 }}<br />{{c^3 + a^3 }} \geqslant \frac{{a + b + c}}<br />{2} \hfill \\<br /> \frac{{a^4 + b^4 + c^4 }}<br />{{a^3 + b^3 + b^3 + c^3 + c^3 + a^3 }} \geqslant \frac{{a + b + c}}<br />{2} \hfill \\<br /> \frac{{a^4 + b^4 + c^4 }}<br />{{2a^3 + 2b^3 + 2c^3 }} \geqslant \frac{{a + b + c}}<br />{2} \hfill \\<br /> \Rightarrow \boxed{\frac{{a^4 }}<br />{{a^3 + b^3 }} + \frac{{b^4 }}<br />{{b^3 + c^3 }} + \frac{{c^4 }}<br />{{c^3 + a^3 }} \geqslant \frac{{a + b + c}}<br />{2}}\blacktriangle \hfill \\ <br />\end{gathered} <br />\]](./tex/f9d9a8361742210f8abac658c6896946.png) Me imagino que ![TEX: \[<br />a,b,c \in \mathbb{R}<br />\]](./tex/ce2309abcc74ea00b4739f7a504fdd2a.png) No me tengo mucha fe, pero igual. Saludos Disculpame que te lo diga, pero tu demostracion esta completamente rara (por no decir otra cosa). Partiste de a,b,c>0 para llegar a a,b,c>0, osea, llegaste a donde partiste  . Es absurdo no crees?. Seria refacil si fuese asi... . Es absurdo no crees?. Seria refacil si fuese asi...Saludos Mensaje modificado por Felipe_ambuli el Jun 11 2008, 08:50 PM |
|
|
|
 Jun 13 2008, 11:31 PM Jun 13 2008, 11:31 PM
Publicado:
#19
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Un hint para los que se han cabesiado nomas!
salu2 Mensaje modificado por pelao_malo el Jun 13 2008, 11:36 PM --------------------  |
|
|
|
 Jun 13 2008, 11:54 PM Jun 13 2008, 11:54 PM
Publicado:
#20
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 170 Registrado: 25-July 07 Miembro Nº: 7.812 |
mmmm... sumatoria simétrica.
¿¿¿Se podría usar Muirhead??? |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 04:24 PM |










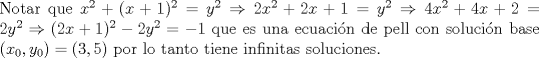
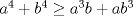 (pruebelo usted mismo, pero no sea bruto =D)
(pruebelo usted mismo, pero no sea bruto =D)