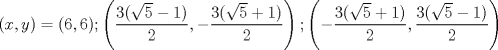|
|
|
|
|
|
|
  |
 Mar 20 2006, 11:29 PM Mar 20 2006, 11:29 PM
Publicado:
#1
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
 Suerte -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Apr 16 2006, 10:37 AM Apr 16 2006, 10:37 AM
Publicado:
#2
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 73 Registrado: 13-April 06 Miembro Nº: 841 |
Idea:
|
|
|
|
 Jan 6 2008, 06:47 PM Jan 6 2008, 06:47 PM
Publicado:
#3
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 82 Registrado: 7-March 07 Desde: Más allá del arcoiris xD Miembro Nº: 4.362 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Ayer soñé con este ejercicio
 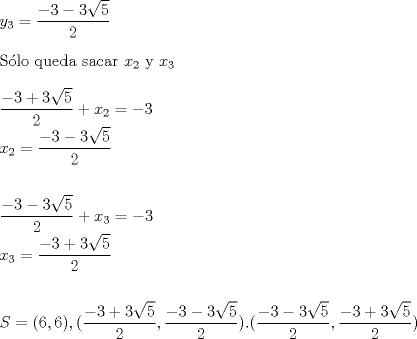
-------------------- Cada persona ha tenido momentos y episodios en su vida que más le valdría no haber superado (Goethe)
|
|
|
|
 Feb 18 2008, 08:50 AM Feb 18 2008, 08:50 AM
Publicado:
#4
|
|
|
Dios Matemático Grupo: Team Ensayos FMAT Mensajes: 311 Registrado: 24-April 07 Miembro Nº: 5.425 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Creo que la respuesta está incorrecta.
Si analizamos el despeje de la primera ecuación, debería quedar: xy (y+x) = 12xy Así, x+y = 12 De esta forma, nos queda que 36=xy lo que tiene infinitas soluciones |
|
|
|
 Feb 18 2008, 11:12 AM Feb 18 2008, 11:12 AM
Publicado:
#5
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 4.857 Registrado: 2-January 08 Miembro Nº: 14.268 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
![TEX: \[<br />\begin{gathered}<br /> a{\text{ ver yo lo hice asi }}{\text{, pero me dio el resultado de las sumas de las incognitas :}} \hfill \\<br /> \frac{{x^2 }}<br />{y} + \frac{{y^2 }}<br />{x} = 12 \Rightarrow \frac{{x^3 + y^3 }}<br />{{xy}} = 12 \Rightarrow \frac{{(x + y)(x^2 - xy + y^2 )}}<br />{{xy}} = 12 \hfill \\<br /> \frac{1}<br />{x} + \frac{1}<br />{y} = \frac{1}<br />{3} \Rightarrow \frac{{x + y}}<br />{{xy}} = \frac{1}<br />{3} \Rightarrow 3(x + y) = xy/()^2 \Rightarrow x^2 + 2xy + y^2 = \frac{{\left( {xy} \right)^2 }}<br />{9} \hfill \\<br /> {\text{reemplazamos lo que nos dio en la segunda ecuacion en la primera}} \hfill \\<br /> {\text{quedandonos:}} \hfill \\<br /> \frac{{(x + y)(x^2 - xy + y^2 )}}<br />{{xy}} = 12 \Rightarrow \frac{{(x + y)(x^2 - xy + y^2 )}}<br />{{3(x + y)}} = 12 \Rightarrow \frac{{x^2 - xy + y^2 }}<br />{1} = 36 \hfill \\<br /> \Leftrightarrow x^2 - xy + y^2 = 36 \Rightarrow x^2 + 2xy + y^2 = 36 + 3xy \Rightarrow (x + y)^2 = 36 + 3xy \hfill \\<br /> reemplazando:xy = 3(x + y) \hfill \\<br /> queda: \hfill \\<br /> (x + y)^2 = 36 + 9(x + y) \Rightarrow (x + y)^2 - 9(x + y) - 36 = 0 \hfill \\<br /> \Leftrightarrow ((x + y) - 12)((x + y) + 3) = 0 \hfill \\<br /> \therefore \left( {x + y} \right)_1 = 12 \wedge (x + y)_2 = - 3 \hfill \\<br /> \hfill \\<br /> \hfill \\<br /> saludos \hfill \\ <br />\end{gathered} <br />\]](./tex/8a26135db6103a252a3c1fcb6fd38ba1.png)
-------------------- Candidato a doctor en Cs. De la ingeniería mención modelamiento matemático, DIM. Universidad de Chile
Magíster en ciencias mención matemática, Profesor de estado en matemáticas y computación, Licenciado en educación matemáticas y computación, USACH |
|
|
|
 Feb 18 2008, 11:46 AM Feb 18 2008, 11:46 AM
Publicado:
#6
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 283 Registrado: 1-July 07 Desde: vallenar Miembro Nº: 7.202 Nacionalidad:  Universidad:  Sexo:  |
 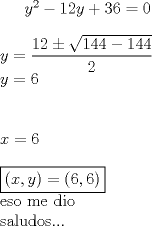
-------------------- |
|
|
|
 Apr 12 2010, 08:04 PM Apr 12 2010, 08:04 PM
Publicado:
#7
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 400 Registrado: 27-October 09 Desde: ¡Qué te importa! Miembro Nº: 61.057 Universidad:  Sexo:  |
Yo creo que tengo una :$
Jajaja.. Dice así.. Si estoy mal, no me pifeen tanto, jajajaja. En la segunda ecuación multiplicamos por 36.. nos queda 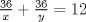 Igualamos en la primera 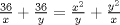 Dejamos 0 a un lado 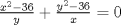 Amplificamos por xy 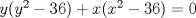 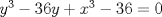 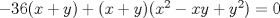 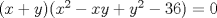 De lo cual se sacan dos ecuaciones nuevas 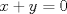 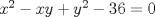 Y.. Bueno, no sé cómo proseguir.. Se me acaba la imaginación, y no tengo herramientas pa' seguir.. |
|
|
|
 Oct 19 2010, 02:12 PM Oct 19 2010, 02:12 PM
Publicado:
#8
|
|
|
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 16 Registrado: 7-June 09 Desde: Osorno, Chile Miembro Nº: 53.342 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Yo obtuve los mismos resultados que virtualivan =)
GoChuck lo dejaste casi listo. Te dejo una pista para que sigas mira tu ultima expresion x2-xy+y2=36 eso escribelo como (x+y)2 -3xy=36 y luego vuelve a las primeras dos ecuaciones que da el problema para reemplazar el -3xy por una expresion equivalente en (x+y).... Despues despeja el valor de (x+y), te recomiendo que utilices a= (x+y) para facilitar el calculo... |
|
|
|
 Jan 13 2015, 11:53 PM Jan 13 2015, 11:53 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 579 Registrado: 17-April 11 Miembro Nº: 87.233 Colegio/Liceo:  Universidad:  Sexo:  |
Otra forma:
Saludos |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 26th April 2025 - 12:12 AM |










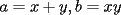
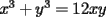
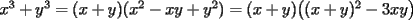
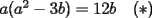
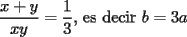
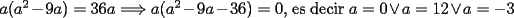

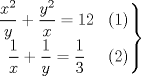
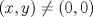
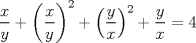
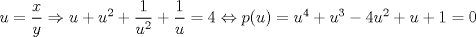
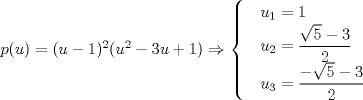
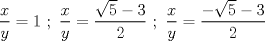
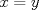 , la cuál reemplazando en
, la cuál reemplazando en 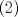 llegamos a que
llegamos a que 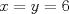 .
.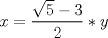 , reemplazando en
, reemplazando en 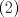 tenemos:
tenemos: 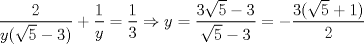
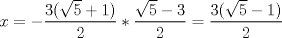 .
.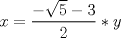 , reemplazando en
, reemplazando en 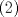 tenemos:
tenemos: 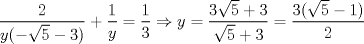
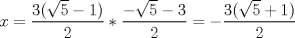 .
.