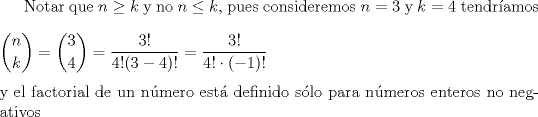|
|
|
|
|
|
|
  |
 Mar 18 2006, 12:21 AM Mar 18 2006, 12:21 AM
Publicado:
#1
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 228 Registrado: 8-August 05 Desde: Santiago de Chile Miembro Nº: 194 |
  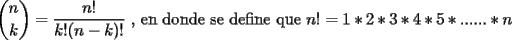 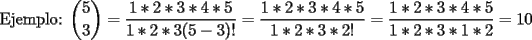 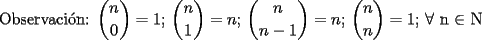 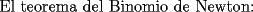 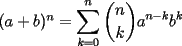 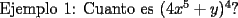 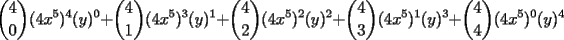 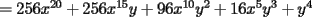 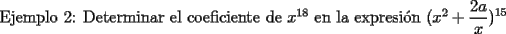 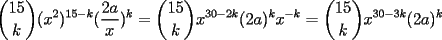 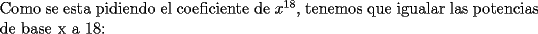 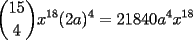 SALU Mensaje modificado por Rurouni Kenshin el Jul 17 2008, 05:22 AM |
|
|
|
 Jul 22 2007, 09:32 PM Jul 22 2007, 09:32 PM
Publicado:
#2
|
|
 Puntaje Nacional PSU Matemáticas Admisión 2010 Grupo: Colaborador Gold Mensajes: 390 Registrado: 22-July 07 Desde: la granja Miembro Nº: 7.754 Nacionalidad:  Colegio/Liceo:  Sexo:  |
al fin entendi lo q queria decir arancibia
-------------------- ...
|
|
|
|
 Sep 1 2007, 10:13 PM Sep 1 2007, 10:13 PM
Publicado:
#3
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 170 Registrado: 25-July 07 Miembro Nº: 7.812 |
Yo conozco otra forma que está en función de lo anterior para desarrollar
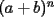 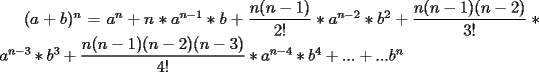 La idea es que el siguiente coeficiente de  y y 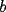 sigan esa lógica. sigan esa lógica.Si 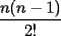 es el cofeciente de es el cofeciente de  y y 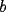 . El siguiente coeficiente será la misma expresión agregándole . El siguiente coeficiente será la misma expresión agregándole  y y 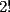 pasa a ser pasa a ser 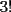 . Al siguiente coeficiente le debo agregar . Al siguiente coeficiente le debo agregar  y y 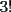 pasa a ser pasa a ser 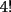 , y así sucesivamente. , y así sucesivamente.Respecto a qué número están elevados  y y 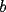 . Los exponentes de ellos deben sumar . Los exponentes de ellos deben sumar  , de manera que al ir desarrollando la expresión, uno exponente va subiendo y el otro exponente va bajando una unidad. Y debe seguir esa lógica. , de manera que al ir desarrollando la expresión, uno exponente va subiendo y el otro exponente va bajando una unidad. Y debe seguir esa lógica. Además si tuviésemos 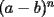 , será el mismo desarrollo. Pero, cuando , será el mismo desarrollo. Pero, cuando 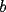 esté elevado a un número impar, la expresión de la que forma parte ese esté elevado a un número impar, la expresión de la que forma parte ese 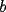 , pasará restando. , pasará restando.
Mensaje modificado por Chaparrón el Sep 2 2007, 07:23 PM |
|
|
|
 Sep 2 2007, 01:56 PM Sep 2 2007, 01:56 PM
Publicado:
#4
|
|
 Maestro Matemático Grupo: Colaborador Silver Mensajes: 128 Registrado: 30-June 06 Desde: En Rio de Janeiro, Brasil Miembro Nº: 1.477 Nacionalidad:  Universidad: .png) Sexo:  |
-------------------- _______________________________________________________________
"La primera regla de la enseñanza es saber lo que se debe enseñar. La segunda, es saber un poco más de aquello que se debe enseñar". George Polya Eu sou uma estudante da UFRJ. |
|
|
|
 Jan 23 2008, 08:27 PM Jan 23 2008, 08:27 PM
Publicado:
#5
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 170 Registrado: 25-July 07 Miembro Nº: 7.812 |
Este teromea es muy útil para no tener que hacer toooooo....oodo el desarrollo
|
|
|
|
 Jan 29 2008, 07:21 PM Jan 29 2008, 07:21 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 752 Registrado: 15-August 07 Desde: Santiago Miembro Nº: 8.770 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
|
|
|
|
 Mar 30 2008, 02:45 PM Mar 30 2008, 02:45 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 4.874 Registrado: 19-January 07 Desde: Mathematics!! Miembro Nº: 3.830 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
--------------------  "... Lo veo, pero no puedo creerlo ... se trata de mostrar que las superficies, los volúmenes e incluso las variedades continuas de n dimensiones pueden ponerse en correspondencia unívoca con curvas continuas, o sea, con variedades de una sola dimensión, y que por consiguiente, las superficies, los volúmenes y las variedades de n dimensiones tienen también la misma potencia que las curvas ..." G. Cantor. Las Matemáticas son el lenguaje de la naturaleza, todo lo que nos rodea se puede representar y entender mediante números. Si se hace un gráfico con los números de un sistema, se forman modelos; éstos modelos están por todas partes en la naturaleza. Max Cohen.  Licenciado en Matemática (2021). Universidad de Concepción, Chile. |
|
|
|
 Jul 16 2008, 11:08 PM Jul 16 2008, 11:08 PM
Publicado:
#8
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 8 Registrado: 20-June 08 Miembro Nº: 27.790 Nacionalidad:  Sexo:  |
|
|
|
|
 Jul 19 2008, 04:13 PM Jul 19 2008, 04:13 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 745 Registrado: 1-October 07 Miembro Nº: 10.754 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
 --------------------  |
|
|
|
 Aug 10 2008, 10:36 PM Aug 10 2008, 10:36 PM
Publicado:
#10
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 55 Registrado: 17-July 07 Desde: Donde nadie mas llega Miembro Nº: 7.619 Nacionalidad:  |
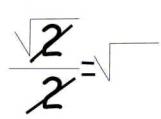
A mi cuando estaba en IV medio, me enseñaron una forma que en la universidad no me la enseñaron y es valida para
N e RACIONALES DISCULPADME ME HE LEIDO UNA Y OTRA VEZ EL LATEX Y AUN NO LO ENTIENDO, ASI QUE OCUPARE EL LENGUAJE DE UN CAS. (a+b)^(p/q) = SUM(conv(n,k)*a^(n-i)*b^i, i , p/q)) Tal que: conv(n,k)=(n(n-1)(n-2)...(n-k+1))/(1*2*3...*k) Hay que tener ojo, ya que para aproximar raices hay que tener experiencia en el tema, me explico: RAIZ(2) = (1+1)^(1/2) Pero cuidado que aveces cuando el a es una raiz o el b es una raiz no siempre es igual. Notese que este desarrollo es infinito, pues veran... i va desde 1 a n pero n es 0,5 entonces i toma los siguientes valores: 1, 2, 3, 4, 5, 6, ... , n cuando n = 0,5 1, 2, 3, 4, 5, 6, ... , (0,5) Aun que paresca absurdo asi es; bueno el n ahora no solo puede ser un natural, si no un racional. SE QUE PARECE COMPLICADO DE ENTENDER QUE UNA SUMATORIA VALLA DE N=1 HASTA UN RACIONAL O INCLUSO UN NEGATIVO!!!!! Y MAS AUN UNA CONVINATORIA CUANDO EL FACTORIAL ESTA DEFINIDO EN |N Y 0, ASI QUE OS DEJO EJEMPLOS EJEMPLO 1 RAIZ(1,01)= (1+0,01)^(1/2) se acuerdan que les dije que el a y el b no pueden ser cualquier numero??? bueno sustituyan a por 0,01 y b=1 y os dara otro resultado erroneo. Segun binomio... (1+10^-2)^(1/2) = 1+(1/2*10^-2)-(1/8*10^-4)+(1/10*10^-6)... = 1+0,005-0,0000125+0,0000000625-0,0000000003905+...= RESPUESTA SEGUN BINOMIO: 1,00498756211... RESPUESTA SEGUN CALCULADORA: 1,00498756211... Nuestro resultado fue muy presiso pero no exacto, ya que tiene una aproximacion, pues si ubiece hecho la suma con los tres primeros numeros me daba: 1,0049875... Y con 4 sumandos... 1,0049875625... Ahi tienen, tambien sirve para numeros negativos DISCULPADME POR NO USAR LATEX, PUES NO ENTIENDO NADA DEL CODIGO, NI CON MANUALES Y TODO, NO ENTIENDO NADA XDDDD, Y TAMBIEN POR QUE ESTA MATERIA ME LA PASARON EN IV MEDIO PLAN DIFERENCIADO, PERO COMO VI EL PRIMER POST CON SUMATORIAS PUES ENTONCES NO SE A QUE NIVEL ESTAN LOS SECUNDARIOS AHORA; PERO LO CURIOSO ES QUE ESTA APLICACION NO ME LA PASARON EN ALGEBRA ELEMENTAL Y SUPERIOR XDDDDDDDDDDD --------------------      |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 10:39 AM |