Sumatorias - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa de Enseñanza Media > 2º Medio > Contenidos 2º Medio

2 Páginas:

1 2 >

Reply to this topic

Start new topic

Sumatorias, lo + básico

tt14123 Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 17 2006, 06:50 PM Publicado: #1
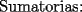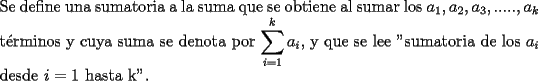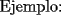Dios Matemático Grupo: Usuario FMAT Mensajes: 228 Registrado: 8-August 05 Desde: Santiago de Chile Miembro Nº: 194	$TEX: Sumatorias:$ $TEX: \noindent Se define una sumatoria a la suma que se obtiene al sumar los $a_1, a_2, a_3, ....., a_k$ t\'erminos y cuya suma se denota por $\displaystyle\sum_{i=1}^{k}a_i$, y que se lee "sumatoria de los $a_i$ desde $i=1$ hasta k".$ $TEX: Ejemplo:$ $TEX: \noindent La expresi\'on $\displaystyle\sum_{i=1}^{30}10i$ nos indica la suma de los m\'ultiplos de 10, desde 10 hasta 300, y es la suma de los 30 sumandos formados por $10+20+30+40+50+ ............. 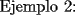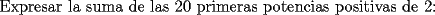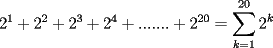+300$$ $TEX: Ejemplo 2:$ $TEX: Expresar la suma de las 20 primeras potencias positivas de 2:$ $TEX: $2^1+2^2+2^3+2^4+ ....... 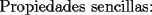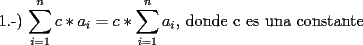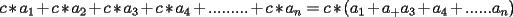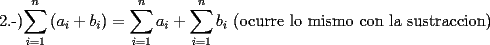+2^{20} = \displaystyle\sum_{k=1}^{20}2^k$$ $TEX: Propiedades sencillas:$ $TEX: 1.-) $\displaystyle\sum_{i=1}^{n}{ca_i} = c\displaystyle\sum_{i=1}^{n}a_i $, donde c es una constante$ $TEX: $ca_1+ca_2+ca_3+ca_4+.........+ca_n = c(a_1+a_+a_3+a_4+......a_n)$$ $TEX: 2.-)$ \displaystyle\sum_{i=1}^{n}{(a_i+b_i)} = \sum_{i=1}^{n}a_i + \displaystyle\sum_{i=1}^{n}b_i$ (ocurre lo mismo con la sustraccion)$ $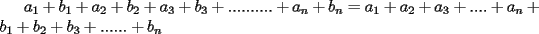TEX: \noindent $a_1+b_1+a_2+b_2+a_3+b_3+..........+a_n+b_n = a_1+a_2+a_3+....+a_n+b_1+b_2+b_3+......+b_n$$ $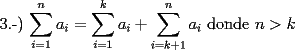TEX: 3.-) $\displaystyle\sum_{i=1}^{n}{a_i} = \displaystyle\sum_{i=1}^{k}{a_i}+\sum_{i=k+1}^{n}{a_i}$ donde $n>k$$ $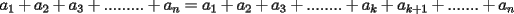TEX: $a_1+a_2+a_3+.........+a_n = a_1+a_2+a_3+........+a_k+a_{k+1}+.......+a_n$$ $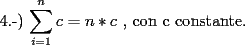TEX: 4.-) $\displaystyle\sum_{i=1}^{n}{c} = nc$ , con c constante.$ $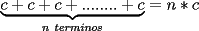TEX: $\underbrace{c+c+c+........+c}_{{n}\ t\'erminos} = nc$$ $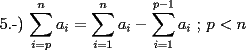TEX: 5.-) $\displaystyle\sum_{i=p}^{n}{a_i} = \displaystyle\sum_{i=1}^{n}{a_i}-\displaystyle\sum_{i=1}^{p-1}{a_i}$ ; $p<n$$ $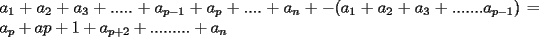TEX: \noindent $a_1+a_2+a_3+.....+a_{p-1}+a_p+....+a_n+-(a_1+a_2+a_3+.......a_{p-1}) = a_p+a{p+1}+a_{p+2}+.........+a_n $$ SALUDOS

tt14123 Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 17 2006, 07:15 PM Publicado: #2
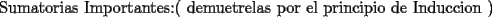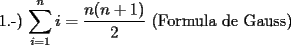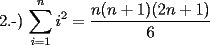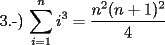Dios Matemático Grupo: Usuario FMAT Mensajes: 228 Registrado: 8-August 05 Desde: Santiago de Chile Miembro Nº: 194	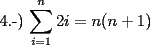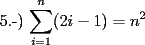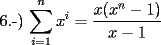$TEX: Sumatorias Importantes:( demuetrelas por el principio de Induccion )$ $TEX: 1.-) $\displaystyle\sum_{i=1}^{n}i = \displaystyle\frac{n(n+1)}{2}$ (Formula de Gauss)$ $TEX: 2.-) $\displaystyle\sum_{i=1}^{n}i^2 = \displaystyle\frac{n(n+1)(2n+1)}{6}$$ $TEX: 3.-) $\displaystyle\sum_{i=1}^{n}i^3 = \displaystyle\frac{n^2(n+1)^2}{4}$$ $TEX: 4.-) $\displaystyle\sum_{i=1}^{n}2i = n(n+1)$$ $TEX: 5.-) $\displaystyle\sum_{i=1}^{n}(2i-1) = n^2$$ $TEX: 6.-) $\displaystyle\sum_{i=1}^{n}x^i = \displaystyle\frac{x(x^n-1)}{x-1}$$ $TEX: 7.-) $\displaystyle\sum_{i=1}^{n}[(i+1)^2-i^2] = (n+1)^2-1^2$ propiedad telescopica$ SALU

tt14123 Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 17 2006, 07:42 PM Publicado: #3
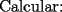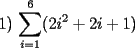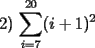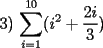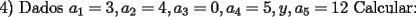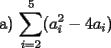Dios Matemático Grupo: Usuario FMAT Mensajes: 228 Registrado: 8-August 05 Desde: Santiago de Chile Miembro Nº: 194	$TEX: Calcular:$ $TEX: 1) $\displaystyle\sum_{i=1}^{6}(2i^2+2i+1)$$ $TEX: 2) $\displaystyle\sum_{i=7}^{20}(i+1)^2$$ $TEX: 3) $\displaystyle\sum_{i=1}^{10}(i^2+\displaystyle\frac{2i}{3})$$ $TEX: 4) Dados $a_1 = 3 , a_2 = 4 , a_3 = 0 , a_4 = 5 ,y , a_5 = 12$ Calcular:$ $TEX: a) $\displaystyle\sum_{i=2}^{5}(a_i^2-4a_i)$$ $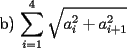TEX: b) $\displaystyle\sum_{i=1}^{4}\sqrt{a_i^2+a_{i+1}^2}$$ $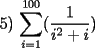TEX: 5) $\displaystyle\sum_{i=1}^{100}(\displaystyle\frac{1}{i^2+i})$$ $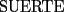TEX: SUERTE$

Guía Rojo Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 18 2006, 08:56 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 903 Registrado: 28-May 05 Desde: Santiago, Chile Miembro Nº: 69 Nacionalidad: Colegio/Liceo: Sexo:	CITA(tt14123 @ Mar 17 2006, 09:15 PM) $TEX: $\displaystyle\sum_{i=1}^{n}[(i+1)^2-i^2] = (n+1)^2-1^2$ propiedad telescopica$ Aquí discrepo contigo, en el punto en que ésta NO es la definición de la sumatoria telescópica... tú tomas un caso especial de la sumatoria... La definición es la siguiente: 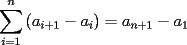$TEX: $\displaystyle\sum_{i=1}^n\left(a_{i+1}-a_i\right)=a_{n+1}-a_1$$ Lo que tú hiciste fue tomar 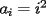$TEX: $a_i=i^2$$ , lo que no está mal, pero no es generalizable... Saludos... -------------------- Bachiller en Ciencias (ex) Estudiante de Medicina Estudiante de Ingeniería Civil de Industrias, diploma en Ingeniería Matemática Pontificia Universidad Católica de Chile "El espíritu del matemático busca la belleza del pensamiento, y esa va de la mano con la filosofía." - Héctor Hardy Pastén Vásquez "¿Qué te hace pensar que si tienes dos elementos de un conjunto con otros dos elementos de otro conjunto se origina uno nuevo con cuatro? Es sólo el sentido común, no te imaginas que los elementos aparecen de la nada, pero resulta que con el sólo hecho de cuestionar el sentido común, se podría afirmar que cuando juntas cuatro elementos aparecen miles de elementos más. Y si lo demuestras, todo se basa en la razón." - Alonso Duque Vega, razonador por excelencia $TEX: $S=1+dfrac{1}{2}+dfrac{1}{3}+dfrac{1}{4}+dfrac{1}{5}+ldots$$ Esta serie converge! He encontrado una maravillosa demostración de esto, pero no cabe en la estrechez de esta firma...

ginobili Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 19 2006, 11:49 AM Publicado: #5
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 178 Registrado: 28-May 05 Desde: Aca , alla , aca , alla Miembro Nº: 70 Nacionalidad: Universidad: Sexo:	Buena Guia gracias.... se me viene fuerte sumatorias en Algebra -------------------- Por un lado la matematica , lo mas importante , pero por el otro el basquetbol y ginobili lo mejor q hay!!!! Team Naranja!!! Apagando incendios xD

tt14123 Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 19 2006, 03:32 PM Publicado: #6
Dios Matemático Grupo: Usuario FMAT Mensajes: 228 Registrado: 8-August 05 Desde: Santiago de Chile Miembro Nº: 194	CITA(Guía Rojo @ Mar 18 2006, 09:56 PM) Aquí discrepo contigo, en el punto en que ésta NO es la definición de la sumatoria telescópica... tú tomas un caso especial de la sumatoria... La definición es la siguiente: 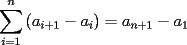$TEX: $\displaystyle\sum_{i=1}^n\left(a_{i+1}-a_i\right)=a_{n+1}-a_1$$ Lo que tú hiciste fue tomar 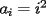$TEX: $a_i=i^2$$ , lo que no está mal, pero no es generalizable... Saludos... Tienes razón; yo lo puse más que nada como ejemplo de la propiedad telescópica y ademas para que practiquen con inducción. SALU

XxryurickxX Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 31 2006, 11:48 AM Publicado: #7
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 166 Registrado: 15-October 06 Desde: desde mi compu en temuco Miembro Nº: 2.532 Nacionalidad: Universidad: Sexo:	$TEX: weno hola$ miren yo no soy bueno con induccion nisiquiera me la pasaron en el cole y como soy medio duro de entendimiento esto es lo que kaxo en induccion: sabemos que eso es la suma de los numeros naturales osea 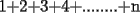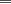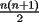$TEX: 1+2+3+4+........+n$ $TEX: =$ $TEX: $\frac{n(n+1)}{2}$$ ahora probemos si se cumple para 1 1=1(1+1)/2 1=1 si funciona ok entonces suponemos que funciona para N = K 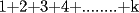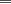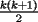$TEX: 1+2+3+4+........+k$ $TEX: =$ $TEX: $\frac{k(k+1)}{2}$$ y deveria cumplirse ok entonces de ahi vemos si se cumple para el siguiente osea 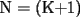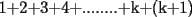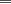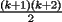$TEX: N = (K+1)$ $TEX: 1+2+3+4+........+k+(k+1)$ $TEX: =$ $TEX: $\frac{(k+1)(k+2)}{2}$$ entonces: 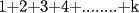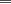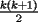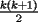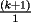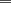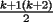$TEX: 1+2+3+4+........+k$ $TEX: =$ $TEX: $\frac{k(k+1)}{2}$$ $TEX: $\frac{k(k+1)}{2}$$ + $TEX: $\frac{(k+1)}{1}$$ $TEX: =$ $TEX: $\frac{(k+1)(k+2)}{2}$$ entonces igualamos denominadores: 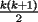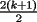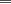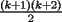$TEX: $\frac{k(k+1)}{2}$$ + $TEX: $\frac{2(k+1)}{2}$$ $TEX: =$ $TEX: $\frac{(k+1)(k+2)}{2}$$ sumamos las fraciones y obtenomos lo siguiente 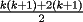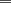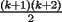$TEX: $\frac{k(k+1)+2(k+1)}{2}$$ $TEX: =$ $TEX: $\frac{(k+1)(k+2)}{2}$$ ahora suprimimos terminos semejantes y nos queda: 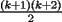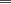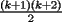$TEX: $\frac{(k+1)(k+2)}{2}$$ $TEX: =$ $TEX: $\frac{(k+1)(k+2)}{2}$$ eso seria corrijame plis por que es mejor equivocarse que no saber nada ok saludos xau -------------------- weno El hombre que en los mas hondo de su ser, duda de sí mismo, jamás encontrará quien lo acompañe [H. Keyserling.] Allí donde se hicieorn los caminos, o he perdido el mio.(XxryurickxX) Defiende tu derecho a pensar, porque incluso pensar en forma errónea es mejor que no pensar (Hipatia) Si buscas resultados distintos, no hagas siempre lo mismo (Albert Einstein)

XxryurickxX Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 31 2006, 12:12 PM Publicado: #8
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 166 Registrado: 15-October 06 Desde: desde mi compu en temuco Miembro Nº: 2.532 Nacionalidad: Universidad: Sexo:	weno por si acaso esos K+1 son factores van entre parentesis osea son (k+1) peor el latrex no me pesca ok -------------------- weno El hombre que en los mas hondo de su ser, duda de sí mismo, jamás encontrará quien lo acompañe [H. Keyserling.] Allí donde se hicieorn los caminos, o he perdido el mio.(XxryurickxX) Defiende tu derecho a pensar, porque incluso pensar en forma errónea es mejor que no pensar (Hipatia) Si buscas resultados distintos, no hagas siempre lo mismo (Albert Einstein)

XxryurickxX Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 31 2006, 03:03 PM Publicado: #9
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 166 Registrado: 15-October 06 Desde: desde mi compu en temuco Miembro Nº: 2.532 Nacionalidad: Universidad: Sexo:	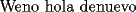$TEX: Weno hola denuevo$ vamos por la segunda patita: bueno creo que la siguiente sumatoria se trata de sumar los cuadrados ahi voy 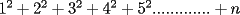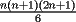$TEX: $1^2+2^2+3^2+4^2+5^2.............+n$$ = $TEX: $\frac{n(n+1)(2n+1)}{6}$$ veamos si se cumple para 1 : 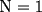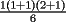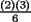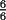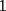$TEX: N = 1$ $TEX: $\frac{1(1+1)(2+1)}{6}$$ $TEX: $\frac{(2)(3)}{6}$$ $TEX: $\frac{6}{6}$$ $TEX: 1$ y vemos que se cumple entonces suponemos que se cumple para 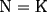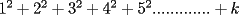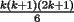$TEX: N = K$ : $TEX: $1^2+2^2+3^2+4^2+5^2.............+k$$ = $TEX: $\frac{k(k+1)(2k+1)}{6}$$ y volvemos a suponer, ahora que se cumple para N = (K+1) 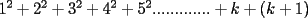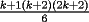$TEX: $1^2+2^2+3^2+4^2+5^2.............+k+(k+1)$$ = $TEX: $\frac{k+1(k+2)(2k+2)}{6}$$ sabemos que: 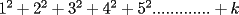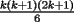$TEX: $1^2+2^2+3^2+4^2+5^2.............+k$$ = $TEX: $\frac{k(k+1)(2k+1)}{6}$$ entonces reducimos esta asi: 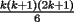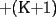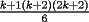$TEX: $\frac{k(k+1)(2k+1)}{6}$$ $TEX: +(K+1)$ = $TEX: $\frac{k+1(k+2)(2k+2)}{6}$$ entonces desarrolloamos la suma: 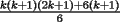$TEX: $\frac{k(k+1)(2k+1)+6(k+1)}{6}$$ [/tex]= $TEX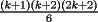: $\frac{(k+1)(k+2)(2k+2)}{6}$$ sumamos las fraciones y nos queda asi: 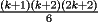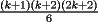$TEX: $\frac{(k+1)(k+2)(2k+2)}{6}$$ = $TEX: $\frac{(k+1)(k+2)(2k+2)}{6}$$ diganme si esta biem por fa un post no les cuesta nada por que creo haberme perdido ok eso seria mi respues ok saludos y si la tengo mala no duden en decirmelo saludos -------------------- weno El hombre que en los mas hondo de su ser, duda de sí mismo, jamás encontrará quien lo acompañe [H. Keyserling.] Allí donde se hicieorn los caminos, o he perdido el mio.(XxryurickxX) Defiende tu derecho a pensar, porque incluso pensar en forma errónea es mejor que no pensar (Hipatia) Si buscas resultados distintos, no hagas siempre lo mismo (Albert Einstein)

Zirou Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 31 2006, 03:25 PM Publicado: #10
Máquina que convierte café en teoremas Grupo: Colaborador Silver Mensajes: 1.665 Registrado: 18-August 05 Desde: Concepción Miembro Nº: 247 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	no estas mal, pero hay un pequeño gran detalle. Las inducciones que aqui piden son a travez de sumatorias y no asi como lo haces. Las soluciones que tu estas colocando mas bien deben ir en este tema que es donde realmente se pide lo que tu haces y aun no estan resueltos. Saludos -------------------- $TEX: $mathcal{Z}$ $imath$ $Re$ $varnothing$ $mho$$ Manual para subir imágenes y archivos a fmat (con servidor propio) Manual de latex Estilo Propio Lista de libros en fmat "Un Matemático es una máquina que trasforma café en teoremas"(Erdös) --- Consultas, sugerencias, reclamos via mp o a los correos mencionados.

« Posterior · Contenidos 2º Medio · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 4th April 2025 - 02:19 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.