Radicales Dobles - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa de Enseñanza Media > 3º Medio > Ejercicios 3º Medio

2 Páginas:

1 2 >

Reply to this topic

Start new topic

Radicales Dobles, Qieres aprender mas????

xdanielx Ver Perfil del Miembro Ver los mensajes de este miembro	May 25 2008, 05:59 PM Publicado: #1
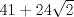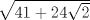Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617	Analizare un ejercicio tipico de diferenciado de 3ero medio.... Se llaman radicales dobles. Son de la forma $TEX: $\sqrt {x \pm \sqrt y }$$ Ejemplo, halle la raiz cuadrada de $TEX: ${41 + 24\sqrt 2 }$$ o sea nos piden hallar el valor numerico de $TEX: $\sqrt {41 + 24\sqrt 2 }$$ , si tienes experiencia podrias encontrar rapidamente una factorizacion en la cual sea un cuadrado de binomio y luego extraer la raiz cuadrada sin ningun problema, pero se presentan casos en que no es muy facil hallar la factorizacion...para ello la resolucion de este ejercicio qedara a cargo de la siguiennte formula: $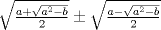TEX: $\sqrt {\frac{{a + \sqrt {a^2 - b} }}{2}} \pm \sqrt {\frac{{a - \sqrt {a^2 - b} }}{2}}$$ Donde a y b representan numeros reales.... Al aplicarla tenemos qe: 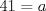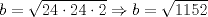$TEX: $41 = a$$ $TEX: $b = \sqrt {24 \cdot 24 \cdot 2} \Rightarrow b = \sqrt {1152}$$ pero solo nos centramos en la cantidad subradical, o sea lo qe va dentro de la raiz.... 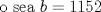$TEX: o sea $b = 1152$$ Al reemplazar los valores en nuestra formula, tenemos: 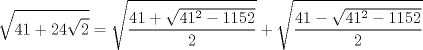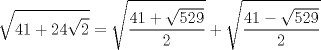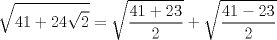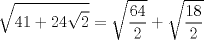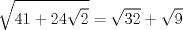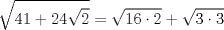$TEX: $$<br />\sqrt {41 + 24\sqrt 2 } = \sqrt {\frac{{41 + \sqrt {41^2 - 1152} }}<br />{2}} + \sqrt {\frac{{41 - \sqrt {41^2 - 1152} }}<br />{2}} <br />$$$ $TEX: $$<br />\sqrt {41 + 24\sqrt 2 } = \sqrt {\frac{{41 + \sqrt {529} }}<br />{2}} + \sqrt {\frac{{41 - \sqrt {529} }}<br />{2}} <br />$$$ $TEX: $$<br />\sqrt {41 + 24\sqrt 2 } = \sqrt {\frac{{41 + 23}}<br />{2}} + \sqrt {\frac{{41 - 23}}<br />{2}} <br />$$$ $TEX: $$<br />\sqrt {41 + 24\sqrt 2 } = \sqrt {\frac{{64}}<br />{2}} + \sqrt {\frac{{18}}<br />{2}} <br />$$$ $TEX: $$<br />\sqrt {41 + 24\sqrt 2 } = \sqrt {32} + \sqrt 9 <br />$$$ $TEX: $$<br />\sqrt {41 + 24\sqrt 2 } = \sqrt {16 \cdot 2} + \sqrt {3 \cdot 3} <br />$$$ por lo tanto 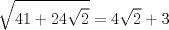$TEX: $$<br />\sqrt {41 + 24\sqrt 2 } = 4\sqrt 2 + 3<br />$$$ Comprobemos 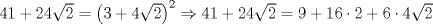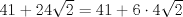$TEX: $41 + 24\sqrt 2 = \left( {3 + 4\sqrt 2 } \right)^2 \Rightarrow 41 + 24\sqrt 2 = 9 + 16 \cdot 2 + 6 \cdot 4\sqrt 2$$ $TEX: $41 + 24\sqrt 2 = 41 + 6 \cdot 4\sqrt 2 $$ Esta igualdad indica qe esta en lo correcto.....Ahora ustedes Halle la raiz cuadrada de 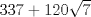$TEX: $337 + 120\sqrt 7$$ Saludos Mensaje modificado por xdanielx el Jan 22 2010, 01:06 PM

edhuardox Ver Perfil del Miembro Ver los mensajes de este miembro	May 29 2008, 12:10 AM Publicado: #2
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 29 Registrado: 26-May 08 Desde: Maipu Miembro Nº: 24.577 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	oooo wena.....no me sabia esa ecuacion pa sacar esas ****...vale men..a puro usarlas no mas --------------------

strange Ver Perfil del Miembro Ver los mensajes de este miembro	May 30 2008, 11:30 PM Publicado: #3
Matemático Grupo: Usuario FMAT Mensajes: 68 Registrado: 16-May 08 Desde: Curicó Miembro Nº: 23.366 Nacionalidad: Sexo:	[font="Courier New"][/font] ns falta todavia ver eso ...

lyonfunky Ver Perfil del Miembro Ver los mensajes de este miembro	May 31 2008, 12:05 AM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 17-February 08 Desde: Santiago Miembro Nº: 15.620 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \[<br />\begin{gathered}<br /> \sqrt {337 + 120\sqrt 7 } \hfill \\<br /> a = 337 \hfill \\<br /> b = 120 \cdot 120 \cdot 7 = 100800 \hfill \\<br /> \sqrt {\frac{{a + \sqrt {a^2 - b} }}<br />{2}} \pm \sqrt {\frac{{a - \sqrt {a^2 - b} }}<br />{2}} \hfill \\<br /> \sqrt {\frac{{337 + \sqrt {337^2 - 100800} }}<br />{2}} + \sqrt {\frac{{337 - \sqrt {337^2 - 100800} }}<br />{2}} \hfill \\<br /> \sqrt {\frac{{337 + \sqrt {12769} }}<br />{2}} + \sqrt {\frac{{337 - \sqrt {12769} }}<br />{2}} \hfill \\<br /> \sqrt {\frac{{337 + 113}}<br />{2}} + \sqrt {\frac{{337 - 113}}<br />{2}} \hfill \\<br /> \sqrt {\frac{{450}}<br />{2}} + \sqrt {\frac{{224}}<br />{2}} \hfill \\<br /> \sqrt {225} + \sqrt {112} \hfill \\<br /> 15 + \sqrt {112} \hfill \\<br /> \boxed{15 + 4\sqrt 7 } \hfill \\ <br />\end{gathered} <br />\]$ wena publikacion -------------------- Estudiante Ingeniería Pontificia Universidad Católica de Chile Admisión 2009 Ex-alumno Colegio Salesiano Oratorio Don Bosco Ex-alumno Preuniversitario Pedro de Valdivia "If this world is turning too fast for your head just remember how bad times can roll instead"

nicogc4 Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 2 2008, 04:51 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 740 Registrado: 9-February 07 Desde: Santiago Miembro Nº: 4.029 Nacionalidad: Universidad: Sexo:	esta muy bueno , no lo habia visto , muchas garcias vivanco --------------------

xdanielx Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 16 2010, 10:29 AM Publicado: #6
Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617	parte dos, alguien puede deducir alguna forma para los radicales del tipo $TEX: $\root 3 \of {x \pm \sqrt y }$$ yo tengo una pero sale de este curso, tiene que ver con ecuaciones cubicas que a veces es trivial resolverlas sabiendo una raiz por tanteo o bajo otros criterios, pero a veces es muy dificil hallarlas, eso ojala alguien se anime y asi podamos continuar con este tema de los radicales dobles saludos Mensaje modificado por xdanielx el Jan 16 2010, 12:32 PM

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 16 2010, 01:06 PM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: <br />$ $\\<br />Para establecer algo como eso hay que demostrar una cantidad bien grande de cosas antes, para lo que justamente esta fmat.\\<br />Seg\'un yo hay que demostrar dos lemitas:\\<br />$ $\\<br />\textbf{Lema 1}: Sean $Q,B,P,Q\in\mathbb{Q}$ tales que ni $B$ ni $Q$ son cuadrados perfectos.\\ <br />Si <br />\begin{eqnarray}<br />A+\sqrt{B}=P+\sqrt{Q}<br />\end{eqnarray}<br />entonces $A=P$ y $B=Q$.\\<br />$ $\\<br />\textbf{Lema 2}: En las hip\'otesis del lema (1).\\<br />Si <br />\begin{eqnarray}<br />A+\sqrt{B}=P+\sqrt{Q}<br />\end{eqnarray}<br />entonces<br />\begin{eqnarray}<br />A-\sqrt{B}=P-\sqrt{Q}<br />\end{eqnarray}<br />Y reci\'en despu\'es 4\textbf{demostrar} la f\'ormula expuesta por xdanielx<br />$ -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

MazTixer Ver Perfil del Miembro Ver los mensajes de este miembro	May 2 2010, 11:51 PM Publicado: #8
Principiante Matemático Grupo: Usuario FMAT Mensajes: 1 Registrado: 13-April 10 Miembro Nº: 68.580 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	La deducción de esta fórmula aparece en las páginas 487 y 488 del Álgebra de Baldor.

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	May 3 2010, 05:04 PM Publicado: #9
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	CITA(MazTixer @ May 2 2010, 11:51 PM) La deducción de esta fórmula aparece en las páginas 487 y 488 del Álgebra de Baldor. jaja ese libro xd puras deducciones de formulas y cero razonamiento -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

Newtype Ver Perfil del Miembro Ver los mensajes de este miembro	May 9 2010, 06:52 PM Publicado: #10
Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad: Sexo:	CITA(Kaissa @ May 3 2010, 06:04 PM) jaja ese libro xd puras deducciones de formulas y cero razonamiento +1 Si quieres aprender a deducir cualquier identidad interesante, lee Baldor, que no explica nada y hace todo para la memorizacion (puedes ver en el foro una demostracion erronea que hace al Teo de Tales), date cuenta de su metodologia, y haz justamente lo contrario... sigue el consejo de Kaissa, a la larga sera mejor, en especial si tiens ramos matematicos en la U, hay que saber pensar, entender de donde sale la idea, entonces tu podras sacar muchaas de estas formulas generales sin memorizarlas, teniendo una idea de como se llega a ella, y a la vez podras llegar a otras. Edit: PD: Igual se nota que no me gusta el Baldor XDD...de hecho pa esas tareas del colegio yo tenia la pauta el libro entero resuelto para copiarlos sin hacerlos XD asi que pesca mi opinion a medias pq es imparcial Mensaje modificado por Hamon el May 9 2010, 06:54 PM -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos

« Posterior · Ejercicios 3º Medio · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 10:27 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.