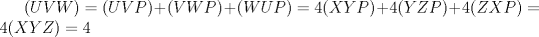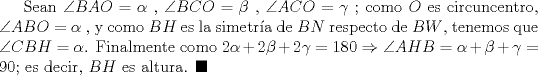|
|
|
|
|
|
|
  |
 May 24 2008, 11:10 PM May 24 2008, 11:10 PM
Publicado:
#1
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
19ª OLIMPIADA DE MATEMÁTICAS DEL CONO SUR Pucón y Lican-Ray, Chile, 2008 Primera Prueba: Martes 20 de mayo de 2008 Problema 1: Se define 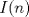 como el resultado de invertir los dígitos del número como el resultado de invertir los dígitos del número  . Por ejemplo, . Por ejemplo, 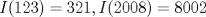 . Encuentre todos los enteros . Encuentre todos los enteros 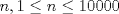 , para los cuales , para los cuales 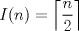 . .Nota:  denota el menor entero mayor o igual que denota el menor entero mayor o igual que  . Por ejemplo, . Por ejemplo, 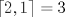 , , 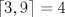 , ,  . .Problema 2: Sea 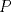 un punto en el interior del triángulo un punto en el interior del triángulo 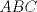 . Sean . Sean 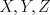 puntos en los lados puntos en los lados 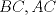 y y 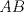 respectivamente, tales que respectivamente, tales que 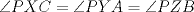 . Sean . Sean 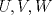 puntos en los lados puntos en los lados 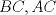 y y 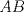 respectivamente, (o en sus extensiones, de ser necesario) con respectivamente, (o en sus extensiones, de ser necesario) con 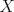 entre entre 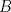 y y 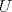 , , 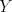 entre entre 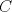 y y 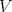 , y , y 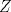 entre entre 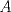 y y 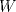 , tales que , tales que 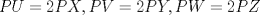 . Si el área del triángulo . Si el área del triángulo 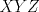 es es 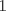 , determinar el área del triángulo , determinar el área del triángulo 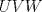 . .Problema 3: Dos amigos 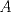 y y 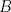 deben resolver el siguiente acertijo. Cada uno de ellos recibe un número del conjunto deben resolver el siguiente acertijo. Cada uno de ellos recibe un número del conjunto  pero no ve el número que recibió el otro. El objetivo es que cada amigo descubra el número del otro. El procedimiento que deben seguir es anunciar, por turnos, números enteros positivos no necesariamente distintos: primero pero no ve el número que recibió el otro. El objetivo es que cada amigo descubra el número del otro. El procedimiento que deben seguir es anunciar, por turnos, números enteros positivos no necesariamente distintos: primero 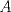 dice un número, luego dice un número, luego 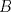 dice un número, a continuación nuevamente dice un número, a continuación nuevamente 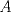 , etc., de modo que la suma de todos los números anunciados sea , etc., de modo que la suma de todos los números anunciados sea 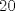 . Demuestre que existe una estrategia por la cual mediante un acuerdo previo . Demuestre que existe una estrategia por la cual mediante un acuerdo previo 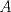 y y 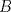 pueden lograr el objetivo, sin importar qué número reciba cada uno al comienzo del acertijo. pueden lograr el objetivo, sin importar qué número reciba cada uno al comienzo del acertijo.Segunda Prueba: Miércoles 21 de mayo de 2008 Problema 4: ¿Cuál es el mayor número de casillas que puede colorearse en un tablero de 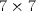 de manera que todo subtablero de de manera que todo subtablero de 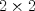 posea a lo más dos casillas coloreadas? posea a lo más dos casillas coloreadas?Problema 5: Sea 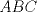 un triángulo isósceles de base un triángulo isósceles de base 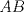 . Una semicircunferencia . Una semicircunferencia 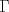 con centro en el segmento con centro en el segmento 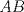 es tangente a los lados iguales es tangente a los lados iguales 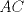 y y 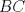 . Se considera una recta tangente a . Se considera una recta tangente a 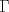 que corta los segmentos que corta los segmentos 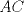 y y 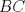 en en 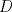 y y 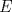 , respectivamente. Suponga que las rectas perpendiculares a , respectivamente. Suponga que las rectas perpendiculares a 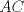 y y 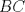 , trazadas respectivamente por , trazadas respectivamente por 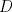 y y 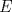 se cortan en un punto se cortan en un punto 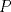 interior al triángulo interior al triángulo 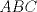 . Sea . Sea 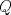 el pie de la perpendicular a la recta el pie de la perpendicular a la recta 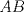 que pasa por que pasa por 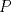 . Demuestre que . Demuestre que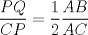 Problema 6: Decimos que un número es capicúa si al invertir el orden de sus c¡fras se obtiene el mismo número. Halle todos los números que tienen al menos un múltiplo que es capicúa. Resumen de soluciones -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 May 25 2008, 04:40 PM May 25 2008, 04:40 PM
Publicado:
#2
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Hints para el P5
Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 May 25 2008, 04:44 PM May 25 2008, 04:44 PM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
Algun hint para el 4
|
|
|
|
 May 25 2008, 04:51 PM May 25 2008, 04:51 PM
Publicado:
#4
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Algun hint para el 4 Hints para el P4 Saludos PD: Me gustaria ver la otra mitad de la prueba -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 May 25 2008, 06:23 PM May 25 2008, 06:23 PM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
Hints para el P4 Saludos PD: Me gustaria ver la otra mitad de la prueba Muchas gracias por los hints. Era algo parecido a lo que estaba intentando, pero ahora lo reflexione mas Solucion Problema 4:      Saludos Mensaje modificado por Felipe_ambuli el May 26 2008, 10:07 AM |
|
|
|
 May 26 2008, 07:55 PM May 26 2008, 07:55 PM
Publicado:
#6
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
Solucion Problema 1:
  Saludos |
|
|
|
 May 26 2008, 08:59 PM May 26 2008, 08:59 PM
Publicado:
#7
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 2: Sea 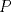 un punto en el interior del triángulo un punto en el interior del triángulo 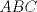 . Sean . Sean 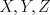 puntos en los lados puntos en los lados 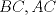 y y 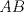 respectivamente, tales que respectivamente, tales que 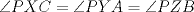 . Sean . Sean 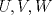 puntos en los lados puntos en los lados 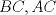 y y 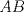 respectivamente, (o en sus extensiones, de ser necesario) con respectivamente, (o en sus extensiones, de ser necesario) con 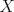 entre entre 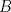 y y 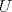 , , 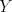 entre entre 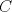 y y 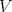 , y , y 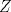 entre entre 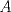 y y 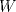 , tales que , tales que 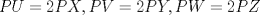 . Si el área del triángulo . Si el área del triángulo 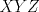 es es 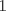 , determinar el área del triángulo , determinar el área del triángulo 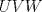 . .Solución al problema 2    Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 May 26 2008, 10:47 PM May 26 2008, 10:47 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
|
|
|
|
 May 27 2008, 01:41 AM May 27 2008, 01:41 AM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Solución P5:
Antes de demostrar el problema; demostraremos el siguiente Lema: Lema: "Al reflejar una altura del triángulo ABC, respecto a la bisectriz que pasa por el mismo vértice; se obtiene la recta que une el circuncentro de ABC con dicho vértice" Demostración:   Saludos |
|
|
|
 Sep 6 2008, 05:35 PM Sep 6 2008, 05:35 PM
Publicado:
#10
|
|
|
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 21 Registrado: 19-July 08 Miembro Nº: 30.254 Nacionalidad:  |
Vou fazer o problema 6, em português, perdão!
6)  Saludos a todos ! |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 09:03 PM |










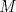 al centro de
al centro de 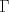 , noten que el Circuncentro del
, noten que el Circuncentro del 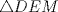 (llamemoslo
(llamemoslo 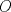 ) pertenece a la Circunferencia Circunscrita al
) pertenece a la Circunferencia Circunscrita al 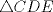 .
. y que
y que 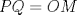 .
.
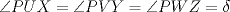 , se tiene que
, se tiene que 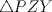 es semejante a
es semejante a 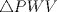 ;
; 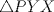 es semejante a
es semejante a 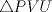 ;
; 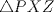 es semejante a
es semejante a 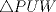 ; todos por criterio de
; todos por criterio de 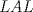 y la razón entre los lados en todos los casos es
y la razón entre los lados en todos los casos es 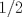 ; por lo tanto:
; por lo tanto: