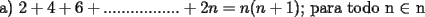|
|
|
|
|
|
|
  |
 Mar 16 2006, 05:14 PM Mar 16 2006, 05:14 PM
Publicado:
#1
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 228 Registrado: 8-August 05 Desde: Santiago de Chile Miembro Nº: 194 |
|
|
|
|
| Corecrasher |
 Mar 16 2006, 05:34 PM Mar 16 2006, 05:34 PM
Publicado:
#2
|
|
Invitado |
 Usaremos induccion , notemos que Usaremos induccion , notemos que 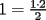 , para , para 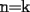 diremos que se cumple que diremos que se cumple que 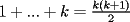 , para , para 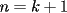 tenemos tenemos 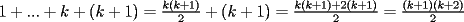 , multiplicando por , multiplicando por  a ambos lados de la igualdad la conclusion es directa a ambos lados de la igualdad la conclusion es directa |
|
|
|
 Mar 16 2006, 09:40 PM Mar 16 2006, 09:40 PM
Publicado:
#3
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 228 Registrado: 8-August 05 Desde: Santiago de Chile Miembro Nº: 194 |
CITA(Corecrasher @ Mar 16 2006, 06:34 PM) 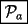 Usaremos induccion , notemos que Usaremos induccion , notemos que 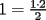 , para , para 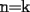 diremos que se cumple que diremos que se cumple que 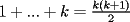 , para , para 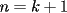 tenemos tenemos 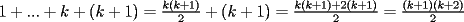 , multiplicando por , multiplicando por  a ambos lados de la igualdad la conclusion es directa a ambos lados de la igualdad la conclusion es directa Esta correcto, pero yo creo que seria mejor que demostraras la suma de los pares directamente por inducción y de manera más ordenada para que los que aun no comprenden bien el tema, puedan manejarse bien con inducción. SALUDOS |
|
|
|
 Mar 17 2006, 09:04 PM Mar 17 2006, 09:04 PM
Publicado:
#4
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 228 Registrado: 8-August 05 Desde: Santiago de Chile Miembro Nº: 194 |
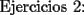  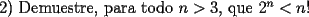 ![TEX: 3) Pruebe por inducci\'on que $[\displaystyle\frac{(n+1)}{n}]^n<n$, para todo $n>2$](./tex/47085.gif)  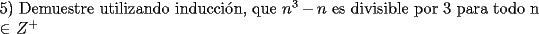 Eso es todo por ahora SALU |
|
|
|
 Nov 8 2007, 08:55 PM Nov 8 2007, 08:55 PM
Publicado:
#5
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 337 Registrado: 14-March 06 Desde: Osorno Miembro Nº: 625 Nacionalidad:  Sexo:  |
Yo vi eso en IVº y en mate electivo :S
-------------------- |
|
|
|
 May 29 2008, 11:22 PM May 29 2008, 11:22 PM
Publicado:
#6
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 260 Registrado: 17-July 07 Desde: por hay Miembro Nº: 7.609 Nacionalidad:  Universidad:  Sexo:  |
no lo sabia gracias
--------------------  |
|
|
|
 Jun 10 2009, 05:57 PM Jun 10 2009, 05:57 PM
Publicado:
#7
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 4 Registrado: 11-April 08 Miembro Nº: 19.777 Nacionalidad:  Colegio/Liceo:  Sexo:  |
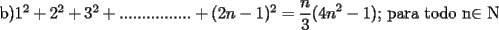 creo que este ejercicio te pide los numeros impares, y hay un par metido entremedio, creo que no debe ir ai sLdos --------------------  |
|
|
|
 Jun 20 2009, 05:18 PM Jun 20 2009, 05:18 PM
Publicado:
#8
|
|
|
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 19 Registrado: 1-May 09 Desde: La Florida Miembro Nº: 49.994 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Yo voy en el Instituto Nacional y me estan pasando demostracion de las propiedades de las potencias x induccion
con el profe Juan carlos Costa xdxdxdxdxd --------------------   |
|
|
|
 Dec 12 2009, 02:45 PM Dec 12 2009, 02:45 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
el primero no requiere mucho trabajo, 2+ 4+6+8....+2n, se puede escribir como 2(1) + 2(2) + 2(3) .... + 2(n), factorizando se obtiene 2(1+2+3+4+5...+n), que es lo mismo que 2(n(n+1)/2), y por reduccion se obtiene n(n+1).
Saludos -------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
 Dec 12 2009, 02:50 PM Dec 12 2009, 02:50 PM
Publicado:
#10
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 387 Registrado: 21-December 08 Desde: Maipu Miembro Nº: 41.103 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Yo voy en el Instituto Nacional y me estan pasando demostracion de las propiedades de las potencias x induccion con el profe Juan carlos Costa xdxdxdxdxd Un ídolo Papi Costa, además de albo de corazón ...xd -------------------- ¿¿¿¿ INTERESAD@ EN CLASES PARTICULARES "Preparación para la PSU" A BAJO COSTO ????
envíar mp " LA LICENCIATURA ES PARA VALIENTES, NO SE ADMITEN COBARDES "     |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 8th July 2025 - 03:29 AM |