Desafio - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Sector PreOlímpico > Álgebra > Problemas Resueltos

2 Páginas:

1 2 >

Reply to this topic

Start new topic

Desafio

Rurouni Kenshin Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 16 2006, 11:15 AM Publicado: #1
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad: Sexo:	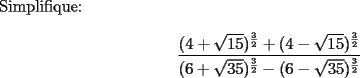$TEX: \noindent Simplifique:\\<br />$$\frac{(4+\sqrt{15})^{\frac{3}{2}}+(4-\sqrt{15})^{\frac{3}{2}}}{(6+\sqrt{35})^{\frac{3}{2}}-(6-\sqrt{35})^{\frac{3}{2}}}$$$ Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!) Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)

caf_tito Ver Perfil del Miembro Ver los mensajes de este miembro	May 14 2006, 11:18 AM Publicado: #2
Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.605 Registrado: 25-June 05 Miembro Nº: 123 Colegio/Liceo: Universidad: Sexo:	screen.width0.6) {this.resized=true; this.width=screen.width0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaÃ±o original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img367.imageshack.us/img367/4649/ecuacin4xt.jpg');}" /> $TEX: \[<br />\begin{gathered}<br /> \frac{{7\left( {\sqrt {4 + \sqrt {15} } + \sqrt {4 - \sqrt {15} } } \right)}}<br />{{13\left( {\sqrt {6 + \sqrt {35} } - \sqrt {6 - \sqrt {35} } } \right)}} \hfill \\<br /> \frac{{49\left[ {\left( {\sqrt {4 + \sqrt {15} } } \right)^2 + 2\left( {\sqrt {4 + \sqrt {15} } } \right)\left( {\sqrt {4 - \sqrt {15} } } \right) + \left( {\sqrt {4 - \sqrt {15} } } \right)^2 } \right]}}<br />{{169\left[ {\left( {\sqrt {6 + \sqrt {35} } } \right)^2 + 2\left( {\sqrt {6 + \sqrt {35} } } \right)\left( {\sqrt {6 - \sqrt {35} } } \right) + \left( {\sqrt {6 - \sqrt {35} } } \right)^2 } \right]}} \hfill \\<br /> \frac{{7\left[ {8 + 2\left( {\sqrt {16 - 15} } \right)} \right]}}<br />{{13\left[ {12 - 2\left( {\sqrt {36 - 35} } \right)} \right]}} \hfill \\<br /> \frac{{7 \cdot 10}}<br />{\begin{gathered}<br /> 13 \cdot 10 \hfill \\<br /> \frac{{7}}<br />{{13}} \hfill \\ <br />\end{gathered} } \hfill \\ <br />\end{gathered} <br />\]$ ahí está editado, ojalá esté bien ahora ahh y se me olvidaba algo, como elevé al cuadrado la fracción aohra extraigo raiz para que no me cambie el valor. $TEX: \[<br />\frac{7}<br />{{13}}<br />\]$ --------------------

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	May 14 2006, 12:54 PM Publicado: #3
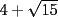Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	No voy a calificar la solución, para no revelar pistas. Pero yo considero que expresiones como $TEX: $4+\sqrt{15}$$ deben mirarse con cuidado para obtener una solución que no sea "mucho leseo" -------------------- Sebastián Elías Puelma Moya Administrador FMAT

hpoincare Ver Perfil del Miembro Ver los mensajes de este miembro	May 16 2006, 03:05 PM Publicado: #4
Maestro Matemático Grupo: Usuario FMAT Mensajes: 73 Registrado: 13-April 06 Miembro Nº: 841	Quizás pueda ayudar: $TEX: $(\sqrt{3}+\sqrt{5})^2=2(4+\sqrt{15})\qquad (\sqrt{5}+\sqrt{7})^2=2(6+\sqrt{35})$$

caf_tito Ver Perfil del Miembro Ver los mensajes de este miembro	May 16 2006, 04:22 PM Publicado: #5
Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.605 Registrado: 25-June 05 Miembro Nº: 123 Colegio/Liceo: Universidad: Sexo:	ahí lo edité, pero = sigo pensando que es musho leseo. --------------------

Gazoo Ver Perfil del Miembro Ver los mensajes de este miembro	May 16 2006, 04:56 PM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.112 Registrado: 21-December 05 Desde: El Bosque - Stgo Miembro Nº: 473 Colegio/Liceo: Universidad: Sexo:	Pero Bastante menos que en el anterior... quitándose una raiz de encima. Yo asi lo veo correcto, pero me gustaria leer el veredicto de Sebastián para enviarlo a resueltos. Saludos -------------------- "El sentido común es el conjunto de todos los prejuicios adquiridos antes de los 18 años" A. Einstein. Estudiante Ingeniería Civil Eléctrica - DIE USACH

「Krizalid」 Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 10 2006, 04:48 PM Publicado: #7
Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad: Sexo:	Notemos que: 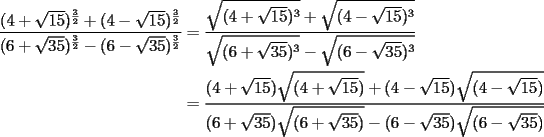$TEX: \begin{equation}<br />\begin{aligned}<br /> \frac{{(4 + \sqrt {15} )^{\frac{3}<br />{2}} + (4 - \sqrt {15} )^{\frac{3}<br />{2}} }}<br />{{(6 + \sqrt {35} )^{\frac{3}<br />{2}} - (6 - \sqrt {35} )^{\frac{3}<br />{2}} }} &= \frac{{\sqrt {(4 + \sqrt {15} )^3 } + \sqrt {(4 - \sqrt {15} )^3 } }}<br />{{\sqrt {(6 + \sqrt {35} )^3 } - \sqrt {(6 - \sqrt {35} )^3 } }} \\ <br /> &= \frac{{(4 + \sqrt {15} )\sqrt {(4 + \sqrt {15} )} + (4 - \sqrt {15} )\sqrt {(4 - \sqrt {15} )} }}<br />{{(6 + \sqrt {35} )\sqrt {(6 + \sqrt {35} )} - (6 - \sqrt {35} )\sqrt {(6 - \sqrt {35} )} }} \\ <br />\end{aligned}<br />\end{equation}$ Ahora bien: 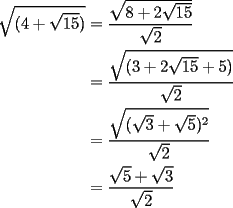$TEX: \begin{equation}<br />\begin{aligned}<br /> \sqrt {(4 + \sqrt {15} )} &= \frac{{\sqrt {8 + 2\sqrt {15} } }}<br />{{\sqrt 2 }} \\ <br /> &= \frac{{\sqrt {(3 + 2\sqrt {15} + 5)} }}<br />{{\sqrt 2 }} \\ <br /> &= \frac{{\sqrt {(\sqrt 3 + \sqrt 5 )^2 } }}<br />{{\sqrt 2 }} \\ <br /> &= \frac{{\sqrt 5 + \sqrt 3 }}<br />{{\sqrt 2 }} \\ <br />\end{aligned}<br />\end{equation}$ Análogamente: 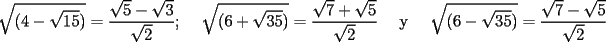$TEX: $$\sqrt {(4 - \sqrt {15} )} = \frac{{\sqrt 5 - \sqrt 3 }}<br />{{\sqrt 2 }}{\text{; \quad }}\sqrt {(6 + \sqrt {35} )} = \frac{{\sqrt 7 + \sqrt 5 }}<br />{{\sqrt 2 }}{\text{ \quad y \quad }}\sqrt {(6 - \sqrt {35} )} = \frac{{\sqrt 7 - \sqrt 5 }}<br />{{\sqrt 2 }}$$$ Finalmente: 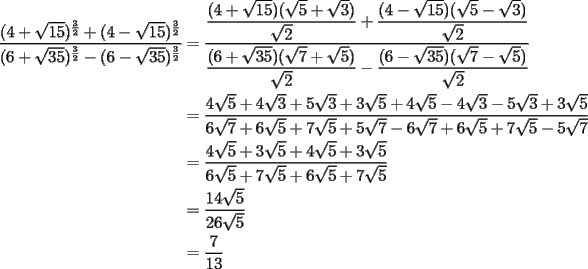$TEX: \begin{equation}<br />\begin{aligned}<br /> \frac{{(4 + \sqrt {15} )^{\frac{3}<br />{2}} + (4 - \sqrt {15} )^{\frac{3}<br />{2}} }}<br />{{(6 + \sqrt {35} )^{\frac{3}<br />{2}} - (6 - \sqrt {35} )^{\frac{3}<br />{2}} }} &= \dfrac{{\dfrac{{(4 + \sqrt {15} )(\sqrt 5 + \sqrt 3 )}}<br />{{\sqrt 2 }} + \dfrac{{(4 - \sqrt {15} )(\sqrt 5 - \sqrt 3 )}}<br />{{\sqrt 2 }}}}<br />{{\dfrac{{(6 + \sqrt {35} )(\sqrt 7 + \sqrt 5 )}}<br />{{\sqrt 2 }} - \dfrac{{(6 - \sqrt {35} )(\sqrt 7 - \sqrt 5 )}}<br />{{\sqrt 2 }}}} \\ <br /> &= \frac{{4\sqrt 5 + 4\sqrt 3 + 5\sqrt 3 + 3\sqrt 5 + 4\sqrt 5 - 4\sqrt 3 - 5\sqrt 3 + 3\sqrt 5 }}<br />{{6\sqrt 7 + 6\sqrt 5 + 7\sqrt 5 + 5\sqrt 7 - 6\sqrt 7 + 6\sqrt 5 + 7\sqrt 5 - 5\sqrt 7 }} \\ <br /> &= \frac{{4\sqrt 5 + 3\sqrt 5 + 4\sqrt 5 + 3\sqrt 5 }}<br />{{6\sqrt 5 + 7\sqrt 5 + 6\sqrt 5 + 7\sqrt 5 }} \\ <br /> &= \frac{{14\sqrt 5 }}<br />{{26\sqrt 5 }} \\ <br /> &= \frac{7}<br />{{13}} \\ <br />\end{aligned}<br />\end{equation}$

picosenotheta Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 14 2007, 10:38 AM Publicado: #8
Dios Matemático Supremo Grupo: Moderador Mensajes: 765 Registrado: 25-November 05 Desde: Algun lugar de la V region Miembro Nº: 415 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Krizalid @ Nov 10 2006, 02:48 PM) Notemos que: $TEX: \begin{equation}<br />\begin{aligned}<br /> \frac{{(4 + \sqrt {15} )^{\frac{3}<br />{2}} + (4 - \sqrt {15} )^{\frac{3}<br />{2}} }}<br />{{(6 + \sqrt {35} )^{\frac{3}<br />{2}} - (6 - \sqrt {35} )^{\frac{3}<br />{2}} }} &= \frac{{\sqrt {(4 + \sqrt {15} )^3 } + \sqrt {(4 - \sqrt {15} )^3 } }}<br />{{\sqrt {(6 + \sqrt {35} )^3 } - \sqrt {(6 - \sqrt {35} )^3 } }} \\ <br /> &= \frac{{(4 + \sqrt {15} )\sqrt {(4 + \sqrt {15} )} + (4 - \sqrt {15} )\sqrt {(4 - \sqrt {15} )} }}<br />{{(6 + \sqrt {35} )\sqrt {(6 + \sqrt {35} )} - (6 - \sqrt {35} )\sqrt {(6 - \sqrt {35} )} }} \\ <br />\end{aligned}<br />\end{equation}$ Ahora bien: $TEX: \begin{equation}<br />\begin{aligned}<br /> \sqrt {(4 + \sqrt {15} )} &= \frac{{\sqrt {8 + 2\sqrt {15} } }}<br />{{\sqrt 2 }} \\ <br /> &= \frac{{\sqrt {(3 + 2\sqrt {15} + 5)} }}<br />{{\sqrt 2 }} \\ <br /> &= \frac{{\sqrt {(\sqrt 3 + \sqrt 5 )^2 } }}<br />{{\sqrt 2 }} \\ <br /> &= \frac{{\sqrt 5 + \sqrt 3 }}<br />{{\sqrt 2 }} \\ <br />\end{aligned}<br />\end{equation}$ Análogamente: $TEX: $$\sqrt {(4 - \sqrt {15} )} = \frac{{\sqrt 5 - \sqrt 3 }}<br />{{\sqrt 2 }}{\text{; \quad }}\sqrt {(6 + \sqrt {35} )} = \frac{{\sqrt 7 + \sqrt 5 }}<br />{{\sqrt 2 }}{\text{ \quad y \quad }}\sqrt {(6 - \sqrt {35} )} = \frac{{\sqrt 7 - \sqrt 5 }}<br />{{\sqrt 2 }}$$$ Finalmente: $TEX: \begin{equation}<br />\begin{aligned}<br /> \frac{{(4 + \sqrt {15} )^{\frac{3}<br />{2}} + (4 - \sqrt {15} )^{\frac{3}<br />{2}} }}<br />{{(6 + \sqrt {35} )^{\frac{3}<br />{2}} - (6 - \sqrt {35} )^{\frac{3}<br />{2}} }} &= \dfrac{{\dfrac{{(4 + \sqrt {15} )(\sqrt 5 + \sqrt 3 )}}<br />{{\sqrt 2 }} + \dfrac{{(4 - \sqrt {15} )(\sqrt 5 - \sqrt 3 )}}<br />{{\sqrt 2 }}}}<br />{{\dfrac{{(6 + \sqrt {35} )(\sqrt 7 + \sqrt 5 )}}<br />{{\sqrt 2 }} - \dfrac{{(6 - \sqrt {35} )(\sqrt 7 - \sqrt 5 )}}<br />{{\sqrt 2 }}}} \\ <br /> &= \frac{{4\sqrt 5 + 4\sqrt 3 + 5\sqrt 3 + 3\sqrt 5 + 4\sqrt 5 - 4\sqrt 3 - 5\sqrt 3 + 3\sqrt 5 }}<br />{{6\sqrt 7 + 6\sqrt 5 + 7\sqrt 5 + 5\sqrt 7 - 6\sqrt 7 + 6\sqrt 5 + 7\sqrt 5 - 5\sqrt 7 }} \\ <br /> &= \frac{{4\sqrt 5 + 3\sqrt 5 + 4\sqrt 5 + 3\sqrt 5 }}<br />{{6\sqrt 5 + 7\sqrt 5 + 6\sqrt 5 + 7\sqrt 5 }} \\ <br /> &= \frac{{14\sqrt 5 }}<br />{{26\sqrt 5 }} \\ <br /> &= \frac{7}<br />{{13}} \\ <br />\end{aligned}<br />\end{equation}$ $TEX: <br /><br />hola <br /><br />aqui va otro metodo <br /><br /><br />Sea <br />\bigskip<br />Z=$\dfrac{(4+\sqrt{15})^{\frac{3}{2}}+(4-\sqrt{15})^{\frac{3}{2}}}{(6+\sqrt{35})^{\frac{3}{2}}-(6-\sqrt{35})^{\frac{3}{2}}}$<br /><br />amplificando por 2 <br />\bigskip<br /><br />Z=$\dfrac{(8+2\sqrt{15})^{\frac{3}{2}}+(8-2\sqrt{15})^{\frac{3}{2}}}{(12+2\sqrt{35})^{\frac{3}{2}}-(12-2\sqrt{35})^{\frac{3}{2}}}$<br /><br />ademas<br /><br /><br />$(8\pm 2\sqrt{15})$ $=(\sqrt{5}\pm \sqrt{3})^{2}$<br /><br />$(12\pm 2\sqrt{35})=(\sqrt{7}\pm \sqrt{5})^{2}$<br /> <br />\bigskip<br /><br /> reemplazando y arreglando exponentes <br /> <br />Z=$\dfrac{(\sqrt{5}+\sqrt{3})^{3}+(\sqrt{5}-\sqrt{3})^{3}}{(\sqrt{7}+\sqrt{5})^{3}-(\sqrt{7}-\sqrt{5})^{3}}$<br /><br />\bigskip <br /><br />desarrollando los cubos de binomio y simplificando <br /><br />Z=$\dfrac{28\sqrt{5}}{52\sqrt{5}}=\allowbreak \dfrac{7}{13}$<br /><br /><br />$ espero comentarios amigos , alguna otra solucion ?? salu2 Mensaje modificado por picosenotheta el Feb 6 2007, 03:23 PM

xdanielx Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 18 2010, 09:17 AM Publicado: #9
Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617	a pedido de picosenotheta notemos que tanto como el numerado y denominador son factorizables 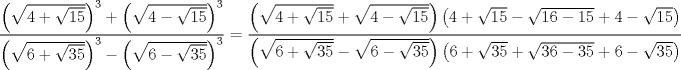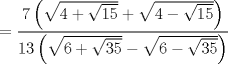$TEX: $$<br />\frac{{\left( {\sqrt {4 + \sqrt {15} } } \right)^3 + \left( {\sqrt {4 - \sqrt {15} } } \right)^3 }}<br />{{\left( {\sqrt {6 + \sqrt {35} } } \right)^3 - \left( {\sqrt {6 - \sqrt {35} } } \right)^3 }} = \frac{{\left( {\sqrt {4 + \sqrt {15} } + \sqrt {4 - \sqrt {15} } } \right)\left( {4 + \sqrt {15} - \sqrt {16 - 15} + 4 - \sqrt {15} } \right)}}<br />{{\left( {\sqrt {6 + \sqrt {35} } - \sqrt {6 - \sqrt {35} } } \right)\left( {6 + \sqrt {35} + \sqrt {36 - 35} + 6 - \sqrt {35} } \right)}}<br />$$$ $TEX: $$<br /> = \frac{{7\left( {\sqrt {4 + \sqrt {15} } + \sqrt {4 - \sqrt {15} } } \right)}}<br />{{13\left( {\sqrt {6 + \sqrt {35} } - \sqrt {6 - \sqrt {35} } } \right)}}<br />$$$ hacemos uso de lo siguiente http://www.fmat.cl/index.php?showtopic=228...mp;#entry408242 quedandonos 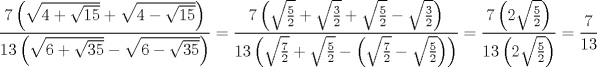$TEX: $$<br />\frac{{7\left( {\sqrt {4 + \sqrt {15} } + \sqrt {4 - \sqrt {15} } } \right)}}<br />{{13\left( {\sqrt {6 + \sqrt {35} } - \sqrt {6 - \sqrt {35} } } \right)}} = \frac{{7\left( {\sqrt {\frac{5}<br />{2}} + \sqrt {\frac{3}<br />{2}} + \sqrt {\frac{5}<br />{2}} - \sqrt {\frac{3}<br />{2}} } \right)}}<br />{{13\left( {\sqrt {\frac{7}<br />{2}} + \sqrt {\frac{5}<br />{2}} - \left( {\sqrt {\frac{7}<br />{2}} - \sqrt {\frac{5}<br />{2}} } \right)} \right)}} = \frac{{7\left( {2\sqrt {\frac{5}<br />{2}} } \right)}}<br />{{13\left( {2\sqrt {\frac{5}<br />{2}} } \right)}} = \frac{7}<br />{{13}}<br />$$$ no lo habia notado mi solucion es muy parecida a la de caftito Mensaje modificado por xdanielx el Jan 18 2010, 09:19 AM

Tela Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 18 2010, 11:42 AM Publicado: #10
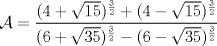Dios Matemático Supremo Grupo: Colaborador Platinum Mensajes: 1.032 Registrado: 25-March 09 Desde: Quinta Normal Miembro Nº: 46.018 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Una solución un "poco" distinta: $TEX: $\displaystyle \mathcal{A} = \frac{(4+\sqrt{15})^{\frac{3}{2}} + (4-\sqrt{15})^{\frac{3}{2}}}{(6+\sqrt{35})^{\frac{3}{2}} - (6-\sqrt{35})^{\frac{3}{2}}}$$ $TEX: Elevamos al cuadrado:$ $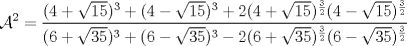TEX: $\displaystyle \mathcal{A}^2 = \frac{(4+\sqrt{15})^{3} + (4-\sqrt{15})^3 + 2(4+\sqrt{15})^{\frac{3}{2}}(4-\sqrt{15})^{\frac{3}{2}}}{(6+\sqrt{35})^{3} + (6-\sqrt{35})^3 - 2(6+\sqrt{35})^{\frac{3}{2}}(6-\sqrt{35})^{\frac{3}{2}}}$$ $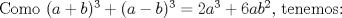TEX: Como $(a+b)^3 + (a-b)^3 = 2a^3 + 6ab^2$, tenemos:$ $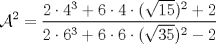TEX: $\displaystyle \mathcal{A}^2 = \frac{2 \cdot 4^3 + 6 \cdot 4 \cdot (\sqrt{15})^2 + 2}{2 \cdot 6^3 + 6 \cdot 6 \cdot (\sqrt{35})^2 - 2}$$ $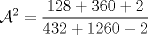TEX: $\displaystyle \mathcal{A}^2 = \frac{128+360+2}{432+1260-2}$$ $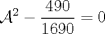TEX: $\displaystyle \mathcal{A}^2 - \frac{490}{1690} = 0$$ $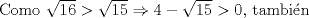TEX: Como $\sqrt{16} > \sqrt{15} \Rightarrow 4 - \sqrt{15} > 0$, también$ $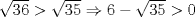TEX: $\sqrt{36} > \sqrt{35} \Rightarrow 6 - \sqrt{35} > 0$$ $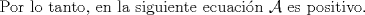TEX: Por lo tanto, en la siguiente ecuación $\mathcal{A}$ es positivo.$ $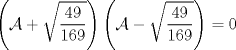TEX: $\displaystyle \left (\mathcal{A} + \sqrt{\frac{49}{169}} \right ) \left (\mathcal{A} - \sqrt{\frac{49}{169}} \right )=0$$ $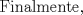TEX: Finalmente,$ $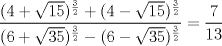TEX: $\displaystyle \frac{(4+\sqrt{15})^{\frac{3}{2}} + (4-\sqrt{15})^{\frac{3}{2}}}{(6+\sqrt{35})^{\frac{3}{2}} - (6-\sqrt{35})^{\frac{3}{2}}} = \frac{7}{13}$$

« Posterior · Problemas Resueltos · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 04:06 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.