Aprendiendo Inducción - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Apuntes y Guías

Reply to this topic

Start new topic

Aprendiendo Inducción

tt14123 Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 14 2006, 04:27 PM Publicado: #1
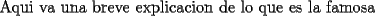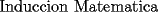Dios Matemático Grupo: Usuario FMAT Mensajes: 228 Registrado: 8-August 05 Desde: Santiago de Chile Miembro Nº: 194	$TEX: Saludos$ $TEX: Aqui va una breve explicacion de lo que es la famosa$ $TEX: Induccion Matematica$ : $TEX: \noindent Primero que nada hay que saber que la Induccion Matematica es un metodo que se ocupa en la demostracion de formulas. 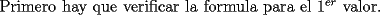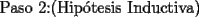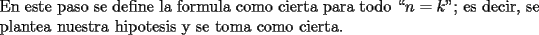Este metodo se basa en la idea de que si la formula se pude realizar para un cierto ``$n$", entonces tiene que ser valida para ``$n+1$", si esto se cumple, entonces la fomula es valida para cualquier valor.$ $TEX: Paso 1:$ $TEX: Primero hay que verificar la formula para el $1^{er}$ valor.$ $TEX: Paso 2:(Hip\'otesis Inductiva)$ $TEX: \noindent En este paso se define la formula como cierta para todo ``$n = k$"; es decir, se plantea nuestra hipotesis y se toma como cierta.$ $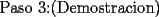TEX: Paso 3:(Demostracion)$ $TEX: \noindent En este paso se busca demostrar que la formula es cierta para todo \mbox{``$n=k+1$"}, pero hay que tener cuidado; en este caso no se parte tomando la formula como cierta para $n = k+1$, sino que hay que tratar de llegar a formula.<br />En este paso se utiliza la hipotesis inductiva para llegar al resultado.$ $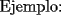TEX: Ejemplo:$ $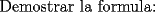TEX: Demostrar la formula:$ $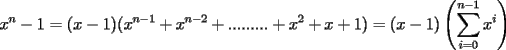TEX: $\displaystyle x^n-1 = (x-1)(x^{n-1}+x^{n-2}+.........+x^2+x+1) = (x-1)\left(\sum_{i=0}^{n-1}x^i\right)$$ $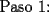TEX: Paso 1:$ $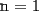TEX: n = 1$ $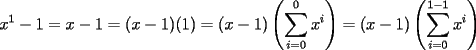TEX: $\displaystyle x^1-1 = x-1 = (x-1)(1) = (x-1)\left(\sum_{i=0}^{0}x^i\right) = (x-1)\left(\sum_{i=0}^{1-1}x^i\right)$$ $TEX: Paso 2:$ $TEX: $n = k$$ $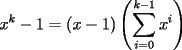TEX: $\displaystyle x^k-1 = (x-1)\left(\sum_{i=0}^{k-1}x^i\right)$$ $TEX: Paso 3:$ $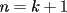TEX: $n = k+1$$ $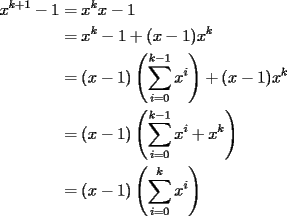TEX: \begin{equation}<br />\begin{aligned}<br />x^{k+1}-1 &= x^kx-1\\ <br />&= x^k-1+(x-1)x^k\\<br />&= (x-1)\left(\sum_{i=0}^{k-1}x^i\right)+(x-1)x^k\\<br />&= (x-1)\left(\sum_{i=0}^{k-1}x^i+x^k\right)\\<br />&= (x-1)\left(\sum_{i=0}^{k}x^i\right)<br />\end{aligned}<br />\end{equation}<br />$ $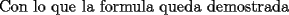TEX: Con lo que la formula queda demostrada$

Corecrasher	Mar 14 2006, 07:08 PM Publicado: #2
Invitado	Buena guia, tal vez tambien seria bueno postear la generalizacion de $TEX: $x_1^n-x_2^n$$

Guía Rojo Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 19 2006, 07:57 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 903 Registrado: 28-May 05 Desde: Santiago, Chile Miembro Nº: 69 Nacionalidad: Colegio/Liceo: Sexo:	Con respecto a la generalización pedida por Corecrasher... pondré lo mío... Caso 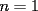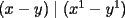$TEX: $n=1$$ $TEX: $\left(x-y\right)\mid \left(x^1-y^1\right)$$ Se cumple... 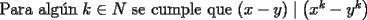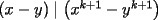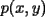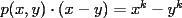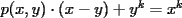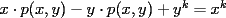Hipótesis de inducción: $TEX: Para alg\'un $k\in N$ se cumple que $\left(x-y\right)\mid \left(x^k-y^k\right)$$ Por demostrar que: $TEX: $\left(x-y\right)\mid \left(x^{k+1}-y^{k+1}\right)$$ Por la hipótesis sabemos que existe un polinomio $TEX: $p(x,y)$$ tal que: $TEX: $p(x,y)\cdot (x-y)=x^k-y^k$$ $TEX: $p(x,y)\cdot (x-y)+y^k=x^k$$ $TEX: $x\cdot p(x,y)-y\cdot p(x,y)+y^k=x^k$$ $TEX: $x\left[x\cdot p(x,y)-y\cdot p(x,y)+y^k\right]=x^{k+1}$$ $TEX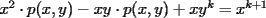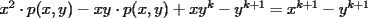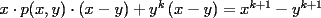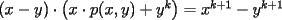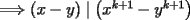: $x^2\cdot p(x,y)-xy\cdot p(x,y)+xy^k=x^{k+1}$$ $TEX: $x^2\cdot p(x,y)-xy\cdot p(x,y)+xy^k-y^{k+1}=x^{k+1}-y^{k+1}$$ $TEX: $x\cdot p(x,y)\cdot \left(x-y\right)+y^k\left(x-y\right)=x^{k+1}-y^{k+1}$$ $TEX: $\left(x-y\right)\cdot \left(x\cdot p(x,y)+y^k\right)=x^{k+1}-y^{k+1}$$ $TEX: $\Longrightarrow (x-y)\mid \left(x^{k+1}-y^{k+1}\right)$$ Demostrando lo pedido... Y probando la generalización pedida por Corecrasher... Saludos... -------------------- Bachiller en Ciencias (ex) Estudiante de Medicina Estudiante de Ingeniería Civil de Industrias, diploma en Ingeniería Matemática Pontificia Universidad Católica de Chile "El espíritu del matemático busca la belleza del pensamiento, y esa va de la mano con la filosofía." - Héctor Hardy Pastén Vásquez "¿Qué te hace pensar que si tienes dos elementos de un conjunto con otros dos elementos de otro conjunto se origina uno nuevo con cuatro? Es sólo el sentido común, no te imaginas que los elementos aparecen de la nada, pero resulta que con el sólo hecho de cuestionar el sentido común, se podría afirmar que cuando juntas cuatro elementos aparecen miles de elementos más. Y si lo demuestras, todo se basa en la razón." - Alonso Duque Vega, razonador por excelencia $TEX: $S=1+dfrac{1}{2}+dfrac{1}{3}+dfrac{1}{4}+dfrac{1}{5}+ldots$$ Esta serie converge! He encontrado una maravillosa demostración de esto, pero no cabe en la estrechez de esta firma...

pancho1901 Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 22 2009, 05:09 PM Publicado: #4
Matemático Grupo: Usuario FMAT Mensajes: 30 Registrado: 31-May 08 Desde: Región de Valparaíso Miembro Nº: 25.298 Nacionalidad: Sexo:	bastante bueno...gracias

« Posterior · Apuntes y Guías · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Versión Lo-Fi

Fecha y Hora actual: 9th April 2025 - 10:02 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.