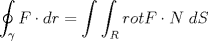|
|
|
|
|
|
|
  |
 Feb 25 2006, 11:51 PM Feb 25 2006, 11:51 PM
Publicado:
#1
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
 Solucion:  Solucion:  Solucion:(Pendiente) 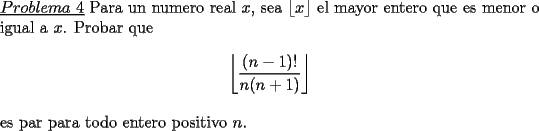 Solucion: 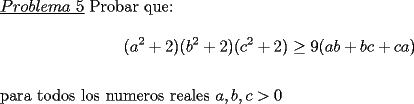 Primera Solucion: Segunda Solucion: Tercera Solucion(Una Desigualdad mas Potente): -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Oct 20 2006, 12:54 PM Oct 20 2006, 12:54 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
-------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Oct 20 2006, 12:58 PM Oct 20 2006, 12:58 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
-------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Nov 17 2009, 07:35 PM Nov 17 2009, 07:35 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo:  Universidad:  Sexo:  |
-------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 20th October 2025 - 06:08 AM |








![TEX: \[<br />\left\lfloor {\frac{{(n - 1)!}}<br />{{n(n + 1)}}} \right\rfloor <br />\]](./tex/69548.gif) para
para  , y en todos los casos obtenemos el valor 0, que es par.
, y en todos los casos obtenemos el valor 0, que es par.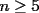 , distinguimos tres casos:
, distinguimos tres casos:![TEX: \[<br />\begin{gathered}<br /> (n - 1)! \equiv n - 1\;(\bmod \;n) \hfill \\<br /> (n - 1)! = nk + n - 1 \hfill \\ <br />\end{gathered} <br />\]](./tex/69551.gif)
 y
y 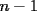 lo son.
lo son.![TEX: \[<br />\begin{gathered}<br /> \frac{{(n - 1)!}}<br />{{n(n + 1)}} = \frac{{(n - 2)!}}<br />{n}\left( {\frac{{n - 1}}<br />{{n + 1}}} \right) = \frac{{(n - 2)!}}<br />{n}\left( {(n - 1) - \frac{{n(n - 1)}}<br />{{n + 1}}} \right) \hfill \\<br /> = \frac{{(n - 1)!}}<br />{n} - \frac{{(n - 1)!}}<br />{{n + 1}} = \frac{{nk + n - 1}}<br />{n} - \frac{{(n - 1)!}}<br />{{n + 1}} = k - \frac{{(n - 1)!}}<br />{{n + 1}} + 1 - \frac{1}<br />{n} \hfill \\ <br />\end{gathered} <br />\]](./tex/69554.gif)
![TEX: \[<br />\frac{{(n - 1)!}}<br />{{n + 1}}<br />\]](./tex/69555.gif)
![TEX: \[<br />\left. {\frac{{(n - 1)!}}<br />{{n + 1}}} \right|_{n = 5} = \frac{{24}}<br />{6} = 4<br />\]](./tex/69556.gif) es verdadero
es verdadero![TEX: \[<br />\frac{{(n - 1)!}}<br />{{n + 1}} \cdot \frac{{n \cdot (n + 1) \cdot (n + 1)}}<br />{{n + 3}} = \frac{{(n + 1)!}}<br />{{n + 3}}<br />\]](./tex/69557.gif)
![TEX: \[<br />\frac{{\overbrace {(n - 1)!}^{2 \cdot 2^{m - 1} \cdot \ldots }}}<br />{{\underbrace {n + 1}_{2 \cdot \ldots }}} \cdot \frac{{n \cdot \overbrace {(n + 1)}^{2 \cdot \ldots } \cdot \overbrace {(n + 1)}^{2 \cdot \ldots }}}<br />{{\underbrace {n + 3}_{2^m \cdot \ldots }}}<br />\]](./tex/69558.gif)
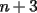 debe ser divisible por alguna potencia de 2 mayor que 2,
debe ser divisible por alguna potencia de 2 mayor que 2,  debe incluir a
debe incluir a 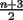 y a 2, luego es divisible por 2.
y a 2, luego es divisible por 2.![TEX: \[<br />\frac{{\overbrace {(n - 1)}^{2^{k - 1} \cdot \ldots }!}}<br />{{\underbrace {n + 1}_{2^k \cdot \ldots }}} \cdot \frac{{n \cdot \overbrace {(n + 1)}^{2^k \cdot \ldots } \cdot \overbrace {(n + 1)}^{2^k \cdot \ldots }}}<br />{{\underbrace {n + 3}_{2 \cdot \ldots }}}<br />\]](./tex/69562.gif)
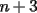 no puede ser divisible por 4, y
no puede ser divisible por 4, y  debe incluir a
debe incluir a 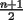 ; luego también es múltiplo de 2 para el caso n+2.
; luego también es múltiplo de 2 para el caso n+2.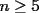
![TEX: \[<br />k - \frac{{(n - 1)!}}<br />{{n + 1}} + 1 - \frac{1}<br />{n}<br />\]](./tex/69567.gif)
![TEX: \[<br />\frac{{n!}}<br />{{(n + 1)(n + 2)}}<br />\]](./tex/69568.gif) es de la forma nº par + nº positivo menor que 1.
es de la forma nº par + nº positivo menor que 1.![TEX: \[<br />\begin{gathered}<br /> \frac{{n!}}<br />{{(n + 1)(n + 2)}} - \frac{{(n - 1)!}}<br />{{n(n + 1)}} = \frac{{(n - 1)!}}<br />{{n + 1}}\left( {\frac{n}<br />{{n + 2}} - \frac{1}<br />{n}} \right) \hfill \\<br /> = \frac{{(n - 1)!(n + 1)(n - 2)}}<br />{{n(n + 1)(n + 2)}} = \frac{{(n - 1)!(n - 2)}}<br />{{n(n + 2)}} \hfill \\ <br />\end{gathered} <br />\]](./tex/69569.gif)
![TEX: \[<br />\frac{{\overbrace {(n - 1)!}^{2 \cdot 2^{m - 1} \cdot \ldots }\overbrace {(n - 2)}^{2^2 \cdot \ldots }}}<br />{{\underbrace n_{2 \cdot \ldots }\underbrace {(n + 2)}_{2^m \cdot \ldots }}}<br />\]](./tex/69570.gif)
![TEX: \[<br />\frac{{\overbrace {(n - 1)!}^{2 \cdot 2 \cdot 2^{k - 1} \cdot \ldots }\overbrace {(n - 2)}^{2 \cdot \ldots }}}<br />{{\underbrace n_{2^k \cdot \ldots }\underbrace {(n + 2)}_{2 \cdot \ldots }}}<br />\]](./tex/69571.gif)
![TEX: \[<br />\frac{{(n - 1)!}}<br />{{n(n + 1)}} = \frac{{n!}}<br />{{(n + 1)(n + 2)}} - \frac{{(n - 1)!(n - 2)}}<br />{{n(n + 2)}}<br />\]](./tex/69572.gif) es de la forma (nº par + nº positivo menor que 1) - nº par = nº par + nº positivo menor que 1, y su parte entera es par. Caso 2 probado.
es de la forma (nº par + nº positivo menor que 1) - nº par = nº par + nº positivo menor que 1, y su parte entera es par. Caso 2 probado.![TEX: \[<br />{\frac{{(n - 1)!}}<br />{{n(n + 1)}}}<br />\]](./tex/69573.gif) es entero, porque tanto los factores de
es entero, porque tanto los factores de  como los de
como los de 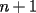 están en
están en  , y como son coprimos no se repiten esos factores.
, y como son coprimos no se repiten esos factores.![TEX: \[<br />\frac{{\overbrace {(n - 1)!}^{2 \cdot 2 \cdot 2^{k - 1} \cdot \ldots }}}<br />{{\underbrace {n(n + 1)}_{2^k \cdot \ldots }}}<br />\]](./tex/69577.gif)
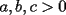 , deben existir
, deben existir 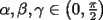 tales que:
tales que: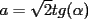 ,
, 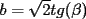 y
y 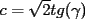 .
.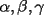 tomaran valores positivos. Esto justificara las desigualdades colocadas a continuacion sin ninguna preocupacion de signo.
tomaran valores positivos. Esto justificara las desigualdades colocadas a continuacion sin ninguna preocupacion de signo. 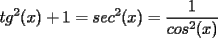 se tendra que la desigualdad a probar(despues de cierto manejo algebraico elemental) es:
se tendra que la desigualdad a probar(despues de cierto manejo algebraico elemental) es:![TEX: $\displaystyle\frac{4}{9}\ge cos(\alpha)cos(\beta)cos(\gamma)[cos(\alpha)cos(\beta)sen(\gamma)+cos(\alpha)sen(\beta)cos(\gamma)+sen(\alpha)cos(\beta)cos(\gamma)]$](./tex/29742.gif)
![TEX: $\displaystyle\frac{4}{9}\ge \underbrace{cos(\alpha)cos(\beta)cos(\gamma)[cos(\alpha)cos(\beta)cos(\gamma)-cos(\alpha+\beta+\gamma)]}_{\displaystyle \mathcal{T}}$](./tex/29755.gif)
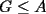 y luego la desigualdad de Jensen (
y luego la desigualdad de Jensen (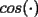 es concava en
es concava en ![TEX: $\displaystyle \left[0,\frac{\pi}{2}\right]$](./tex/29737.gif) )tendremos que:
)tendremos que: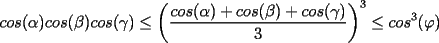
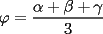
![TEX: $\mathcal{T}\le cos^3(\varphi)[cos^3(\varphi)-cos(3\varphi)]$](./tex/29756.gif)
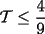
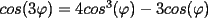 cuya demostracion queda propuesta en el siguiente
cuya demostracion queda propuesta en el siguiente 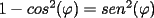 ):
):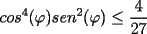
![TEX: $\displaystyle \sqrt[3]{\frac{cos^2(\varphi)}{2}\frac{cos^2(\varphi)}{2}sen^2(\varphi)}\le \frac{\frac{cos^2(\varphi)}{2}+\frac{cos^2(\varphi)}{2}+sen^2(\varphi)}{3}=\frac{1}{3}$](./tex/29762.gif)
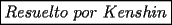
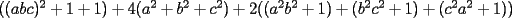
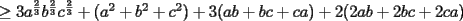
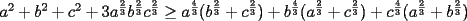
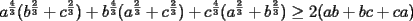
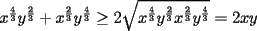
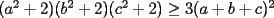
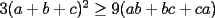 lo cual indica que la desigualdad a probar es "mas exigente" que la original.
lo cual indica que la desigualdad a probar es "mas exigente" que la original.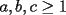 , tendremos que
, tendremos que 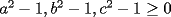 (el mismo signo), por lo tanto:
(el mismo signo), por lo tanto: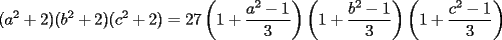
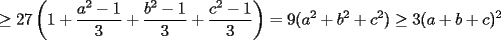
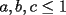 es analogo al Caso 1, pues en ese caso
es analogo al Caso 1, pues en ese caso 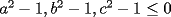 (el mismo signo)
(el mismo signo)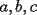 . hay dos de ellos menores o iguales que 1, y uno mayor o igual que 1 ( Digamos
. hay dos de ellos menores o iguales que 1, y uno mayor o igual que 1 ( Digamos 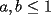 y
y 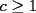 )
)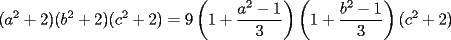
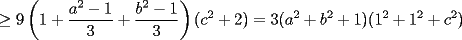
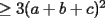
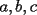 . hay uno de ellos menor o igual que 1, y dos mayores o iguales que 1.
. hay uno de ellos menor o igual que 1, y dos mayores o iguales que 1.






![TEX: \noindent \underline{$Problema\ 1'$} Determine todos los conjuntos finitos no vacíos $S$ de enteros positivos que satisfacen:<br />\\$$(\forall i,j\in S)\ \frac{i+j}{[i,j]}\in S$$\\<br />donde $[i,j]$ es el mínimo común multiplo de $i$ y $j$.](./tex/4020977546bf6fb4dd1a27798c0b058d.png)